|
1 |
The lines 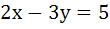 and and 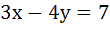 are diameters of a circle of area 154 square units. Then the equation of the circle is are diameters of a circle of area 154 square units. Then the equation of the circle is a) 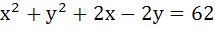 b) 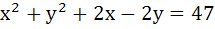 c) 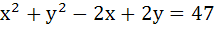 d) 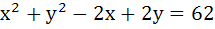
The lines 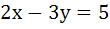 and and 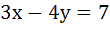 are diameters of a circle of area 154 square units. Then the equation of the circle is are diameters of a circle of area 154 square units. Then the equation of the circle is a) 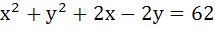 b) 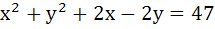 c) 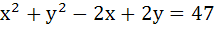 d) 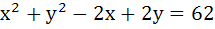
|
IIT 1989 |
03:02 min
|
|
2 |
If α + β =  and β + γ = α, then tanα equals and β + γ = α, then tanα equals a) 2(tanβ + tanγ) b) tanβ + tanγ c) tanβ + 2tanγ d) 2tanβ + tanγ
If α + β =  and β + γ = α, then tanα equals and β + γ = α, then tanα equals a) 2(tanβ + tanγ) b) tanβ + tanγ c) tanβ + 2tanγ d) 2tanβ + tanγ
|
IIT 2001 |
02:03 min
|
|
3 |
Let n be a positive integer and
(1 + x + x2)n = a0 + a1x + a2x + a2x2 + . . . + a2nx2n then prove that
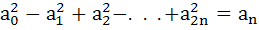
Let n be a positive integer and
(1 + x + x2)n = a0 + a1x + a2x + a2x2 + . . . + a2nx2n then prove that
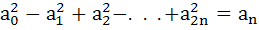
|
IIT 1994 |
06:48 min
|
|
4 |
Evaluate 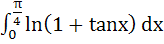 a) πln2 b) 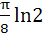 c) 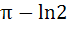 d) 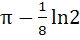
Evaluate 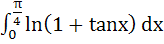 a) πln2 b) 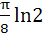 c) 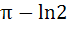 d) 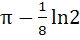
|
IIT 1997 |
02:50 min
|
|
5 |
The angle between a pair of tangents drawn from a point P to the circle 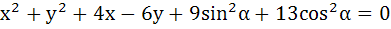 is 2α. Then the locus of P is is 2α. Then the locus of P is a) 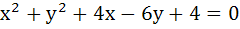 b) 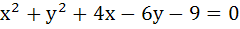 c) 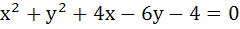 d) 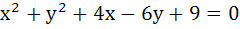
The angle between a pair of tangents drawn from a point P to the circle 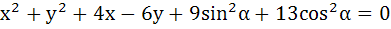 is 2α. Then the locus of P is is 2α. Then the locus of P is a) 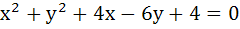 b) 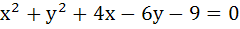 c) 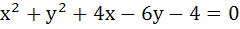 d) 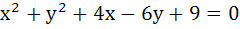
|
IIT 1996 |
05:15 min
|
|
6 |
If 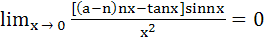 where n is a non–zero real number, then a is equal to where n is a non–zero real number, then a is equal to a) 0 b) 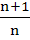 c) n d) 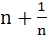
If 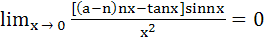 where n is a non–zero real number, then a is equal to where n is a non–zero real number, then a is equal to a) 0 b) 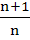 c) n d) 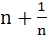
|
IIT 2003 |
02:22 min
|
|
7 |
If f (x) is an even function then prove that
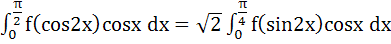 . .
If f (x) is an even function then prove that
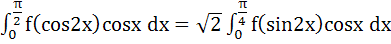 . .
|
IIT 2003 |
07:55 min
|
|
8 |
If A, B, C are three non-coplanar vectors then
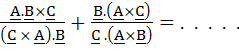
If A, B, C are three non-coplanar vectors then
|
IIT 1985 |
02:22 min
|
|
9 |
The triangle PQR is inscribed in the circle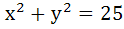 . If Q and R have coordinates (3, 4) and (-4, 3) respectively, then the ∠QPR is equal to . If Q and R have coordinates (3, 4) and (-4, 3) respectively, then the ∠QPR is equal to a)  b)  c) 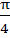 d) 
The triangle PQR is inscribed in the circle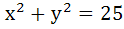 . If Q and R have coordinates (3, 4) and (-4, 3) respectively, then the ∠QPR is equal to . If Q and R have coordinates (3, 4) and (-4, 3) respectively, then the ∠QPR is equal to a)  b)  c) 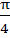 d) 
|
IIT 2000 |
02:46 min
|
|
10 |
The larger of 9950 + 10050 and 10150 is
The larger of 9950 + 10050 and 10150 is
|
IIT 1982 |
04:38 min
|
|
11 |
The projection of a vector a along and perpendicular to a non-zero vector 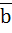 are . . . . . and . . . . . respectively. are . . . . . and . . . . . respectively.
The projection of a vector a along and perpendicular to a non-zero vector 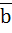 are . . . . . and . . . . . respectively. are . . . . . and . . . . . respectively.
|
IIT 1988 |
03:53 min
|
|
12 |
If the tangent at the point P on the circle 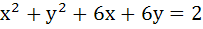 meets the straight line meets the straight line 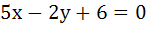 at a point Q on the Y-axis, then the length of PˆQ is at a point Q on the Y-axis, then the length of PˆQ is a) 4 b) 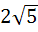 c) 5 d) 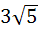
If the tangent at the point P on the circle 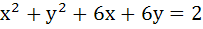 meets the straight line meets the straight line 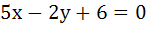 at a point Q on the Y-axis, then the length of PˆQ is at a point Q on the Y-axis, then the length of PˆQ is a) 4 b) 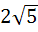 c) 5 d) 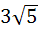
|
IIT 2002 |
01:46 min
|
|
13 |
The integral 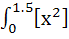 dx where [ ] denotes the greatest integer function equals . . . dx where [ ] denotes the greatest integer function equals . . . a) 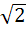 b) 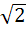 + 1 + 1 c) 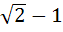 d) 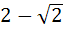
The integral 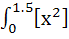 dx where [ ] denotes the greatest integer function equals . . . dx where [ ] denotes the greatest integer function equals . . . a) 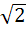 b) 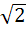 + 1 + 1 c) 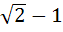 d) 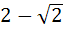
|
IIT 1988 |
02:11 min
|
|
14 |
A non-zero vector a is parallel to the line of intersection of the plane determined by the vectors 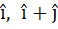 and the plane determined by the vectors and the plane determined by the vectors 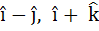 . The angle between a and . The angle between a and 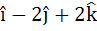 is . . . . . is . . . . .
|
IIT 1996 |
06:39 min
|
|
15 |
A circle is given by 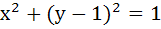 , another circle C touches it externally and also the X-axis, then the locus of the centre of C is , another circle C touches it externally and also the X-axis, then the locus of the centre of C is a) 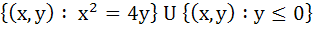 b) 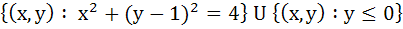 c) 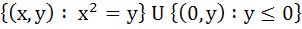 d) 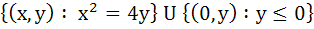
A circle is given by 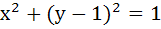 , another circle C touches it externally and also the X-axis, then the locus of the centre of C is , another circle C touches it externally and also the X-axis, then the locus of the centre of C is a) 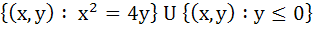 b) 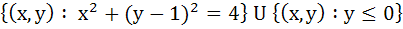 c) 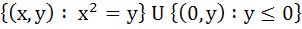 d) 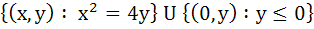
|
IIT 2005 |
05:02 min
|
|
16 |
Find all solutions of
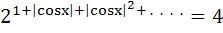 in in 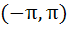 a) 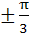 b) 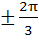 c) 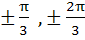 d) 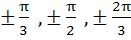
Find all solutions of
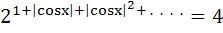 in in 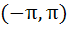 a) 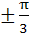 b) 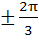 c) 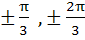 d) 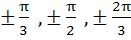
|
IIT 1984 |
03:20 min
|
|
17 |
Let f (x) = sin x and g (x) = ln|x|. If the range of the composition functions fog and gof are R1 and R2 respectively, then a) R1 = [ u : −1 ≤ u < 1], R2 = [ v : −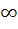 < v < 0 ] < v < 0 ] b) R1 = [ u : −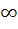 < u < 0 ], R2 = [ v : −1 ≤ v ≤ 0] < u < 0 ], R2 = [ v : −1 ≤ v ≤ 0] c) R1 = [ u : −1 < u < 1], R2 = [ v : −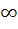 < v < 0 ] < v < 0 ] d) R1 = [ u : −1 ≤ u ≤ 1], R2 = [ v : −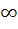 < v ≤ 0 ] < v ≤ 0 ]
Let f (x) = sin x and g (x) = ln|x|. If the range of the composition functions fog and gof are R1 and R2 respectively, then a) R1 = [ u : −1 ≤ u < 1], R2 = [ v : −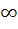 < v < 0 ] < v < 0 ] b) R1 = [ u : −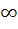 < u < 0 ], R2 = [ v : −1 ≤ v ≤ 0] < u < 0 ], R2 = [ v : −1 ≤ v ≤ 0] c) R1 = [ u : −1 < u < 1], R2 = [ v : −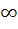 < v < 0 ] < v < 0 ] d) R1 = [ u : −1 ≤ u ≤ 1], R2 = [ v : −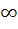 < v ≤ 0 ] < v ≤ 0 ]
|
IIT 1994 |
03:03 min
|
|
18 |
Let f (x) = 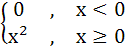 then for all x then for all x a) 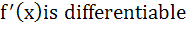 b) f is differentiable c) 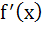 is continuous is continuous d) f is continuous
Let f (x) = 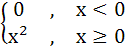 then for all x then for all x a) 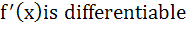 b) f is differentiable c) 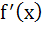 is continuous is continuous d) f is continuous
|
IIT 1994 |
04:05 min
|
|
19 |
If for non-zero x, 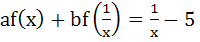 where a ≠ b then where a ≠ b then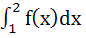 is equal to is equal to a) 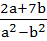 b) 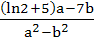 c) 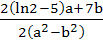 d) 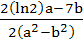
If for non-zero x, 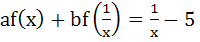 where a ≠ b then where a ≠ b then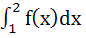 is equal to is equal to a) 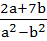 b) 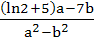 c) 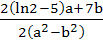 d) 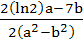
|
IIT 1996 |
04:39 min
|
|
20 |
Find the equation of the circle which passes through the point (2, 0) and whose centre is the limit of the point of intersection of the lines 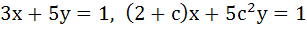 . .
Find the equation of the circle which passes through the point (2, 0) and whose centre is the limit of the point of intersection of the lines 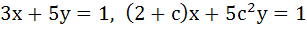 . .
|
IIT 1979 |
06:56 min
|
|
21 |
Multiple choices If f (x) =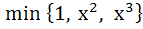 then then a) f (x) is continuous ∀ x 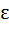 ℝ ℝ b) f (x) > 0 ∀ x > 1 c) f (x) is continuous but not differentiable ∀ x 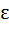 ℝ ℝ d) f (x) is not differentiable at two points
Multiple choices If f (x) =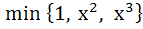 then then a) f (x) is continuous ∀ x 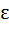 ℝ ℝ b) f (x) > 0 ∀ x > 1 c) f (x) is continuous but not differentiable ∀ x 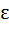 ℝ ℝ d) f (x) is not differentiable at two points
|
IIT 2006 |
04:20 min
|
|
22 |
Eight chairs are numbered one to eight. Two women and three men wish to occupy one chair each. First the women choose the chairs from amongst the chairs marked 1 to 4 then the men select the chairs from amongst the remaining. The number of possible arrangements is a) 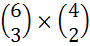 b) 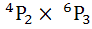 c) 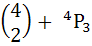 d) None of these
Eight chairs are numbered one to eight. Two women and three men wish to occupy one chair each. First the women choose the chairs from amongst the chairs marked 1 to 4 then the men select the chairs from amongst the remaining. The number of possible arrangements is a) 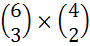 b) 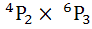 c) 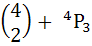 d) None of these
|
IIT 1982 |
01:42 min
|
|
23 |
AB is a diameter of a circle and C is any point on the circumference of the circle. Then a) The area of △ABC is maximum if it is isosceles b) The area of △ABC is minimum if it is isosceles c) The perimeter of △ABC is minimum when it is isosceles d) None of these
AB is a diameter of a circle and C is any point on the circumference of the circle. Then a) The area of △ABC is maximum if it is isosceles b) The area of △ABC is minimum if it is isosceles c) The perimeter of △ABC is minimum when it is isosceles d) None of these
|
IIT 1983 |
05:50 min
|
|
24 |
The abscissas of two points A and B are the roots of the equation 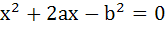 and their ordinates are the roots of the equation and their ordinates are the roots of the equation 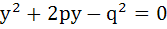 . Find the equation of the circle on AB as diameter. . Find the equation of the circle on AB as diameter.
The abscissas of two points A and B are the roots of the equation 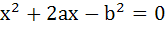 and their ordinates are the roots of the equation and their ordinates are the roots of the equation 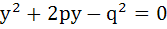 . Find the equation of the circle on AB as diameter. . Find the equation of the circle on AB as diameter.
|
IIT 1984 |
04:47 min
|
|
25 |
Find 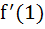 if f(x) = if f(x) = 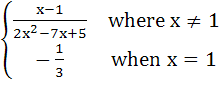 a) 0 b)  c) 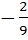 d) 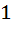
Find 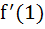 if f(x) = if f(x) = 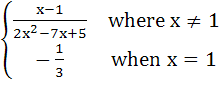 a) 0 b)  c) 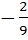 d) 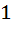
|
IIT 1979 |
02:21 min
|