|
976 |
A rectangle with sides (2m – 1) and (2n – 1) is divided into squares of unit length by drawing parallel lines. Then the number of rectangles possible with odd side lengths is a) mn (m + 1)(n + 1) b) 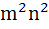 c) 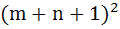 d) 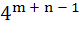
A rectangle with sides (2m – 1) and (2n – 1) is divided into squares of unit length by drawing parallel lines. Then the number of rectangles possible with odd side lengths is a) mn (m + 1)(n + 1) b) 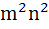 c) 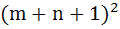 d) 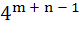
|
IIT 2005 |
|
|
977 |
Find the values of a and b, so that the functions 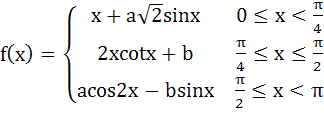
Is continuous for 0 ≤ x ≤ π a) 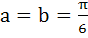 b) 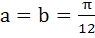 c) 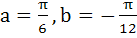 d) 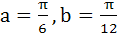
Find the values of a and b, so that the functions 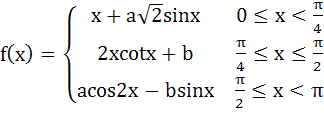
Is continuous for 0 ≤ x ≤ π a) 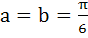 b) 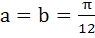 c) 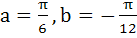 d) 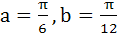
|
IIT 1989 |
|
|
978 |
Let α ε ℝ, then a function f : ℝ → ℝ is differentiable at α if and only if there is a function g : ℝ → ℝ which is continuous at α and satisfies f(x) – f(α) = g(x) (x – α) for all x ε ℝ. a) True b) False
Let α ε ℝ, then a function f : ℝ → ℝ is differentiable at α if and only if there is a function g : ℝ → ℝ which is continuous at α and satisfies f(x) – f(α) = g(x) (x – α) for all x ε ℝ. a) True b) False
|
IIT 2001 |
|
|
979 |
If two functions f and g satisfy the given conditions  x, y ε ℝ, f(x – y) = f(x)g(y) – f(y)g(x) and g(x – y) = g(x) . g(y) + f(x) . f(y). x, y ε ℝ, f(x – y) = f(x)g(y) – f(y)g(x) and g(x – y) = g(x) . g(y) + f(x) . f(y). If the RHD at x = 0 exists for f(x) then find the derivative of g(x) at x = 0.
If two functions f and g satisfy the given conditions  x, y ε ℝ, f(x – y) = f(x)g(y) – f(y)g(x) and g(x – y) = g(x) . g(y) + f(x) . f(y). x, y ε ℝ, f(x – y) = f(x)g(y) – f(y)g(x) and g(x – y) = g(x) . g(y) + f(x) . f(y). If the RHD at x = 0 exists for f(x) then find the derivative of g(x) at x = 0.
|
IIT 2005 |
|
|
980 |
Let 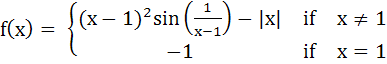 be a real valued function. The set of points where f(x) is not differentiable are a) {0} b) {1} c) {0, 1} d) {∅}
Let 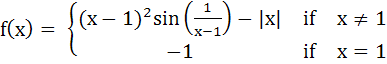 be a real valued function. The set of points where f(x) is not differentiable are a) {0} b) {1} c) {0, 1} d) {∅}
|
IIT 1981 |
|
|
981 |
Let f(x) = [x]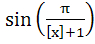 where [.] denotes the greatest integer function. Then the domain of f is . . . ., points of discontinuity of f are . . . . where [.] denotes the greatest integer function. Then the domain of f is . . . ., points of discontinuity of f are . . . . a) ∀ x ε I b) ∀ x ε I − {0} c) ∀ x ε I – {0, 1} d) ∀ x ε I – {0, 1, 2}
Let f(x) = [x]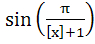 where [.] denotes the greatest integer function. Then the domain of f is . . . ., points of discontinuity of f are . . . . where [.] denotes the greatest integer function. Then the domain of f is . . . ., points of discontinuity of f are . . . . a) ∀ x ε I b) ∀ x ε I − {0} c) ∀ x ε I – {0, 1} d) ∀ x ε I – {0, 1, 2}
|
IIT 1996 |
|
|
982 |
PQ and PR are two infinite rays, QAR is an arc.
Points lying in the shaded region excluding the boundary satisfies a) |z + 1| > 2; |arg(z + 1)| < 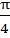 b) |z + 1| < 2; |arg(z + 1)| <  c) 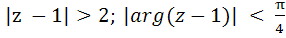 d) 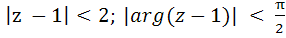
PQ and PR are two infinite rays, QAR is an arc. Points lying in the shaded region excluding the boundary satisfies a) |z + 1| > 2; |arg(z + 1)| < 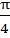 b) |z + 1| < 2; |arg(z + 1)| <  c) 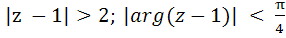 d) 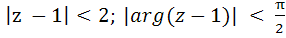
|
IIT 2005 |
|
|
983 |
If a continuous function f defined on the real line ℝ, assumes positive and negative values in ℝ then the equation f(x) = 0 has a root in ℝ. For example, it is known that if a continuous function f on ℝ is positive at some points and its minimum value is negative then the equation f(x) = 0 has a root in ℝ. Consider the function f(x) = 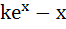 for all real x where k is a real constant. for all real x where k is a real constant. The positive value of k for which 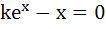 has only one root is has only one root is a)  b) 1 c) e d) ln2
If a continuous function f defined on the real line ℝ, assumes positive and negative values in ℝ then the equation f(x) = 0 has a root in ℝ. For example, it is known that if a continuous function f on ℝ is positive at some points and its minimum value is negative then the equation f(x) = 0 has a root in ℝ. Consider the function f(x) = 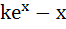 for all real x where k is a real constant. for all real x where k is a real constant. The positive value of k for which 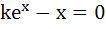 has only one root is has only one root is a)  b) 1 c) e d) ln2
|
IIT 2007 |
|
|
984 |
Let the complex numbers 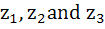 are vertices of an equilateral triangle. If are vertices of an equilateral triangle. If 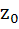 be the circumcentre of the triangle, then prove that be the circumcentre of the triangle, then prove that 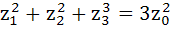
|
IIT 1981 |
|
|
985 |
Let 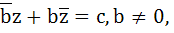 be a line in the complex plane where be a line in the complex plane where 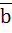 is the complex conjugate of b. If a point is the complex conjugate of b. If a point 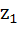 is the deflection of a point is the deflection of a point 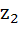 through the line, show that through the line, show that 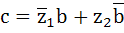 . .
|
IIT 1997 |
|
|
986 |
Which of the following function is periodic? a) f(x) = x – [x] where [x] denotes the greatest integer less than equal to the real number x b) 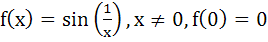 c) f(x) = x cos(x) d) None of these
Which of the following function is periodic? a) f(x) = x – [x] where [x] denotes the greatest integer less than equal to the real number x b) 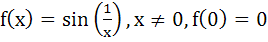 c) f(x) = x cos(x) d) None of these
|
IIT 1983 |
|
|
987 |
If p(x) = 51x101 – 2323x100 – 45x + 1035, using Rolle’s theorem prove that at least one root lies between 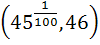 . .
If p(x) = 51x101 – 2323x100 – 45x + 1035, using Rolle’s theorem prove that at least one root lies between 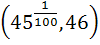 . .
|
IIT 2004 |
|
|
988 |
Given 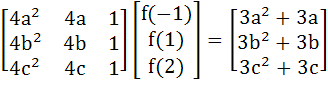
and f(x) is a quadratic polynomial. V is a point of maximum of f(x) and ‘A’ is the point where f(x) cuts the X–axis. ‘B’ is a point such that AB subtends a right angle at V. Find the area between chord AB and f(x).
a) 125 b) 125/2 c) 125/3 d) 125/6
Given 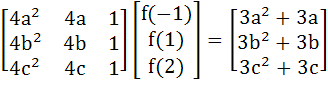
and f(x) is a quadratic polynomial. V is a point of maximum of f(x) and ‘A’ is the point where f(x) cuts the X–axis. ‘B’ is a point such that AB subtends a right angle at V. Find the area between chord AB and f(x).
a) 125 b) 125/2 c) 125/3 d) 125/6
|
IIT 2005 |
|
|
989 |
The area enclosed within the curve |x| + |y| = 1 is . . . a) 1 b) 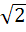 c) 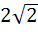 d) 2
The area enclosed within the curve |x| + |y| = 1 is . . . a) 1 b) 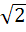 c) 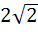 d) 2
|
IIT 1981 |
|
|
990 |
Let g(x) be a function of x defined on (−1, 1). If the area of the equilateral triangle with two of its vertices as (0, 0) and [x, g(x)] is 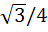 , then the function g(x) is , then the function g(x) is a) 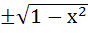 b) 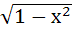 c) 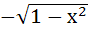 d) None of the above
Let g(x) be a function of x defined on (−1, 1). If the area of the equilateral triangle with two of its vertices as (0, 0) and [x, g(x)] is 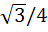 , then the function g(x) is , then the function g(x) is a) 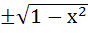 b) 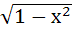 c) 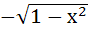 d) None of the above
|
IIT 1989 |
|
|
991 |
Show that the integral of 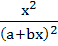 is is 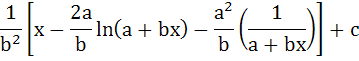
Show that the integral of 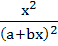 is is 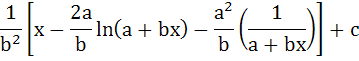
|
IIT 1979 |
|
|
992 |
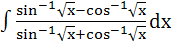 = = 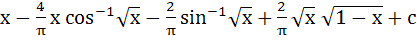
a) True b) False
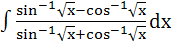 = = 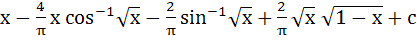
a) True b) False
|
IIT 1986 |
|
|
993 |
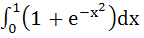
a) – 1 b) 2 c) 1 + e−1 d) None of these
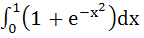
a) – 1 b) 2 c) 1 + e−1 d) None of these
|
IIT 1981 |
|
|
994 |
Let f(x) be differentiable on the interval (0, ∞) such that f (1) = 1 and 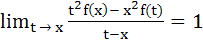 for each x > 0. Then f(x) is for each x > 0. Then f(x) is a) 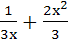 b) 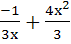 c) 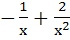 d) 
Let f(x) be differentiable on the interval (0, ∞) such that f (1) = 1 and 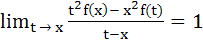 for each x > 0. Then f(x) is for each x > 0. Then f(x) is a) 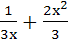 b) 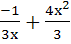 c) 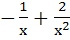 d) 
|
IIT 2007 |
|
|
995 |
Consider the circle x2 + y2 = 9 and the parabola y2 = 8x. They intersect P and Q in the first and fourth quadrants respectively. Tangents to the circle at P and Q intersect the X–axis at R and tangents to the parabola at P and Q intersect the X- axis at S. The radius of the incircle of △PQR is a) 4 b) 3 c)  d) 2
Consider the circle x2 + y2 = 9 and the parabola y2 = 8x. They intersect P and Q in the first and fourth quadrants respectively. Tangents to the circle at P and Q intersect the X–axis at R and tangents to the parabola at P and Q intersect the X- axis at S. The radius of the incircle of △PQR is a) 4 b) 3 c)  d) 2
|
IIT 2007 |
|
|
996 |
Find all possible values of b > 0, so that the area of the bounded region enclosed between the parabolas 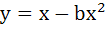 and and 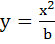 is maximum. is maximum. a) b = 1 b) b ≥ 1 c) b ≤ 1 d) 0 < b < 1
Find all possible values of b > 0, so that the area of the bounded region enclosed between the parabolas 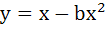 and and 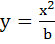 is maximum. is maximum. a) b = 1 b) b ≥ 1 c) b ≤ 1 d) 0 < b < 1
|
IIT 1997 |
|
|
997 |
Let C1 and C2 be the graph of the function y = x2 and y = 2x respectively. Let C3 be the graph of the function
y = f (x), 0 ≤ x ≤ 1, f (0) = 0. Consider a point P on C1. Let the lines through P, parallel to the axes meet C2 and C3 at Q and R respectively (see figure). If for every position of P (on C1) the area of the shaded regions OPQ and OPR are equal, determine the function f(x). 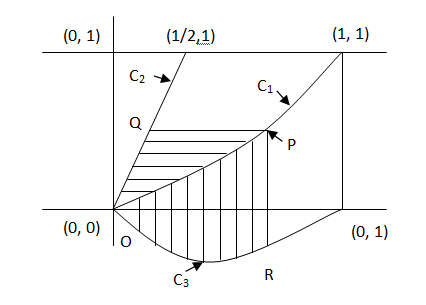
a) x2 – 1 b) x3 – 1 c) x3 – x2 d) 1 + x2 + x3
Let C1 and C2 be the graph of the function y = x2 and y = 2x respectively. Let C3 be the graph of the function
y = f (x), 0 ≤ x ≤ 1, f (0) = 0. Consider a point P on C1. Let the lines through P, parallel to the axes meet C2 and C3 at Q and R respectively (see figure). If for every position of P (on C1) the area of the shaded regions OPQ and OPR are equal, determine the function f(x). 
a) x2 – 1 b) x3 – 1 c) x3 – x2 d) 1 + x2 + x3
|
IIT 1998 |
|
|
998 |
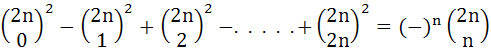
|
IIT 1978 |
|
|
999 |
Let P be a point on the ellipse 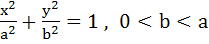 . Let the line parallel to Y–axis passing through P meets the circle . Let the line parallel to Y–axis passing through P meets the circle 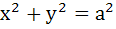 at the point Q such that P and Q are on the same side of the X–axis. For two positive real numbers r and s find the locus of the point R on PQ such that PˆR : RˆQ = r : s and P varies over the ellipse. at the point Q such that P and Q are on the same side of the X–axis. For two positive real numbers r and s find the locus of the point R on PQ such that PˆR : RˆQ = r : s and P varies over the ellipse.
Let P be a point on the ellipse 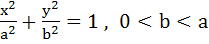 . Let the line parallel to Y–axis passing through P meets the circle . Let the line parallel to Y–axis passing through P meets the circle 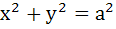 at the point Q such that P and Q are on the same side of the X–axis. For two positive real numbers r and s find the locus of the point R on PQ such that PˆR : RˆQ = r : s and P varies over the ellipse. at the point Q such that P and Q are on the same side of the X–axis. For two positive real numbers r and s find the locus of the point R on PQ such that PˆR : RˆQ = r : s and P varies over the ellipse.
|
IIT 2001 |
|
|
1000 |
If (1 + x)n = C0 + C1x + C2x2 + . . . + Cnxn, then show that the sum of the products of the Cj’s is taken two at a time represented by
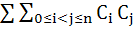 is equal to is equal to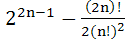
If (1 + x)n = C0 + C1x + C2x2 + . . . + Cnxn, then show that the sum of the products of the Cj’s is taken two at a time represented by
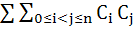 is equal to is equal to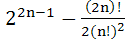
|
IIT 1983 |
|