|
1026 |
One or more than one correct answer Let P and Q be distinct points on the parabola y2 = 2x such that the circle with PQ as diameter passes through the vertex O of the parabola. If P lies in the first quadrant and the area of triangle OPQ is then which of the following is/are the coordinates of P? a) b) c) d)
One or more than one correct answer Let P and Q be distinct points on the parabola y2 = 2x such that the circle with PQ as diameter passes through the vertex O of the parabola. If P lies in the first quadrant and the area of triangle OPQ is then which of the following is/are the coordinates of P? a) b) c) d)
|
IIT 2015 |
|
|
1027 |
The area (in square units) of the region described by A = {(x, y) : x2 + y2 ≤ 1 and y2 ≤ 1 – x} is a) b) c) d)
The area (in square units) of the region described by A = {(x, y) : x2 + y2 ≤ 1 and y2 ≤ 1 – x} is a) b) c) d)
|
IIT 2014 |
|
|
1028 |
If the straight line x = b divides the area enclosed by y = (1 – x)2 , y = 0 and x = 0 into two parts R1 (0 ≤ x ≤ b) and R2 (b ≤x ≤ 1) such that then b equals a) b) c) d)
If the straight line x = b divides the area enclosed by y = (1 – x)2 , y = 0 and x = 0 into two parts R1 (0 ≤ x ≤ b) and R2 (b ≤x ≤ 1) such that then b equals a) b) c) d)
|
IIT 2011 |
|
|
1029 |
Let f(x) be differentiable on the interval (0, ∞) such that f (1) = 1 and 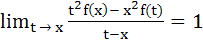 for each x > 0. Then f(x) is for each x > 0. Then f(x) is a) 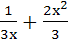 b) 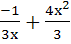 c) 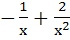 d) 
Let f(x) be differentiable on the interval (0, ∞) such that f (1) = 1 and 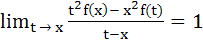 for each x > 0. Then f(x) is for each x > 0. Then f(x) is a) 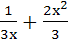 b) 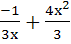 c) 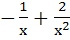 d) 
|
IIT 2007 |
|
|
1030 |
If y = y(x) satisfies the differential equation and Then y(256) = a) 16 b) 3 c) 9 d) 80
If y = y(x) satisfies the differential equation and Then y(256) = a) 16 b) 3 c) 9 d) 80
|
IIT 2017 |
|
|
1031 |
A lot contains 20 articles. The probability that the lot contains exactly 2 defective articles is 0.4 and the probability that the lot contains exactly three defective articles is 0.6. Articles are drawn from the lot at random one by one without replacement and tested till defective articles are found. What is the probability that the testing will end at the 12th testing?
A lot contains 20 articles. The probability that the lot contains exactly 2 defective articles is 0.4 and the probability that the lot contains exactly three defective articles is 0.6. Articles are drawn from the lot at random one by one without replacement and tested till defective articles are found. What is the probability that the testing will end at the 12th testing?
|
IIT 1986 |
|
|
1032 |
If the curve y = f(x) passes through the point (1, −1) and satisfies the differential equation y(1 + xy) dx = xdy then is equal to a) b) c) d)
If the curve y = f(x) passes through the point (1, −1) and satisfies the differential equation y(1 + xy) dx = xdy then is equal to a) b) c) d)
|
IIT 2016 |
|
|
1033 |
One or more than one correct options Let f : (0, ∞) → ℝ be a differentiable function such that for all x ∈ (0, ∞) and f(1) ≠ 1. Then a) b) c) d)
One or more than one correct options Let f : (0, ∞) → ℝ be a differentiable function such that for all x ∈ (0, ∞) and f(1) ≠ 1. Then a) b) c) d)
|
IIT 2016 |
|
|
1034 |
If 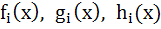 , i = 1, 2, 3 are polynomials in x such that , i = 1, 2, 3 are polynomials in x such that 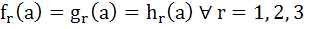 and and F(x) = 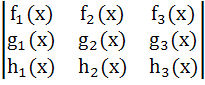
then 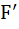 (x) at x = a is equal to (x) at x = a is equal to a) – 1 b) 0 c) 1 d) 2
If 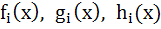 , i = 1, 2, 3 are polynomials in x such that , i = 1, 2, 3 are polynomials in x such that 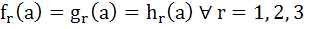 and and F(x) = 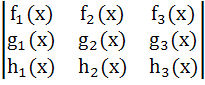
then 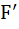 (x) at x = a is equal to (x) at x = a is equal to a) – 1 b) 0 c) 1 d) 2
|
IIT 1985 |
|
|
1035 |
If 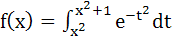 then f (x) increases in then f (x) increases in a) (−2, 2) b) No value of x c) (0, ∞) d) (−∞, 0)
If 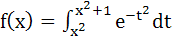 then f (x) increases in then f (x) increases in a) (−2, 2) b) No value of x c) (0, ∞) d) (−∞, 0)
|
IIT 2003 |
|
|
1036 |
A curve passes through the point . Let the slope of the curve at each point (x, y) is , x > 0. Then the equation of the curve is a) b) c) d)
A curve passes through the point . Let the slope of the curve at each point (x, y) is , x > 0. Then the equation of the curve is a) b) c) d)
|
IIT 2013 |
|
|
1037 |
The points 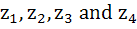 in the complex plane are the vertices of a parallelogram if and only if in the complex plane are the vertices of a parallelogram if and only if a) 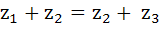 b) 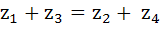 c) 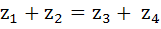 d) None of these
The points 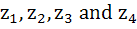 in the complex plane are the vertices of a parallelogram if and only if in the complex plane are the vertices of a parallelogram if and only if a) 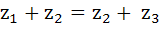 b) 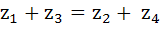 c) 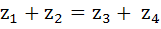 d) None of these
|
IIT 1983 |
|
|
1038 |
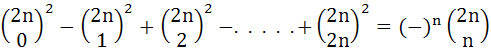
|
IIT 1978 |
|
|
1039 |
Let f:[0, 1] → ℝ (the set all real numbers)be a function. Suppose the function is twice differentiable, f(0) = f(1) = 0 and satisfiesf′′(x) – 2f′(x) + f(x) ≥ ex, x ∈ [0, 1]Which of the following is true? a) b) c) d)
Let f:[0, 1] → ℝ (the set all real numbers)be a function. Suppose the function is twice differentiable, f(0) = f(1) = 0 and satisfiesf′′(x) – 2f′(x) + f(x) ≥ ex, x ∈ [0, 1]Which of the following is true? a) b) c) d)
|
IIT 2013 |
|
|
1040 |
If ω(≠1) is a cube root of unity and 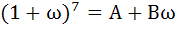 then A and B are respectively then A and B are respectively a) 0, 1 b) 1, 1 c) 1, 0 d) – 1, 1
If ω(≠1) is a cube root of unity and 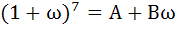 then A and B are respectively then A and B are respectively a) 0, 1 b) 1, 1 c) 1, 0 d) – 1, 1
|
IIT 1995 |
|
|
1041 |
If (1 + x)n = C0 + C1x + C2x2 + . . . + Cnxn, then show that the sum of the products of the Cj’s is taken two at a time represented by
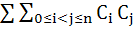 is equal to is equal to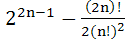
If (1 + x)n = C0 + C1x + C2x2 + . . . + Cnxn, then show that the sum of the products of the Cj’s is taken two at a time represented by
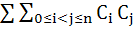 is equal to is equal to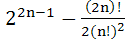
|
IIT 1983 |
|
|
1042 |
Let a, b, c and d be non-zero real numbers. If the point of intersection of lines 4ax + 2ay + c = 0 and 5bx + 2by + d = 0 lie in the fourth quadrants and is equidistant from the two axes, then a) 2bc – 3ad = 0 b) 2bc + 3ad = 0 c) 2ad – 3bc = 0 d) 3bc + 2ad = 0
Let a, b, c and d be non-zero real numbers. If the point of intersection of lines 4ax + 2ay + c = 0 and 5bx + 2by + d = 0 lie in the fourth quadrants and is equidistant from the two axes, then a) 2bc – 3ad = 0 b) 2bc + 3ad = 0 c) 2ad – 3bc = 0 d) 3bc + 2ad = 0
|
IIT 2014 |
|
|
1043 |
One or more than one correct option Let α, λ, μ ∈ ℝ. Consider the system of linear equations αx + 2y = λ 3x – 2y = μWhich of the following statements is/are correct? a) If α = −3, then the system has infinitely many solutions for all values of λ and μ b) If α ≠ −3, then the system of equations has a unique solution for all values of λ and μ c) If λ + μ = 0, then the system has infinitely many solutions for α = −3 d) If λ + μ ≠ 0, then the system has no solution for α = −3
One or more than one correct option Let α, λ, μ ∈ ℝ. Consider the system of linear equations αx + 2y = λ 3x – 2y = μWhich of the following statements is/are correct? a) If α = −3, then the system has infinitely many solutions for all values of λ and μ b) If α ≠ −3, then the system of equations has a unique solution for all values of λ and μ c) If λ + μ = 0, then the system has infinitely many solutions for α = −3 d) If λ + μ ≠ 0, then the system has no solution for α = −3
|
IIT 2016 |
|
|
1044 |
Let 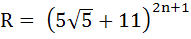 and f = R – [R] where [ ] denotes the greatest integer function. Prove that Rf = 42n + 4 and f = R – [R] where [ ] denotes the greatest integer function. Prove that Rf = 42n + 4
Let 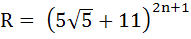 and f = R – [R] where [ ] denotes the greatest integer function. Prove that Rf = 42n + 4 and f = R – [R] where [ ] denotes the greatest integer function. Prove that Rf = 42n + 4
|
IIT 1988 |
|
|
1045 |
One or more than one correct option Circle(s) touching X – axis at a distance 3 from the origin and having an intercept of length on Y – axis is/are a) x2 + y2 – 6x + 8y + 9 = 0 b) x2 + y2 – 6x + 7y + 9 = 0 c) x2 + y2 – 6x − 8y + 9 = 0 d) x2 + y2 – 6x − 7y + 9 = 0
One or more than one correct option Circle(s) touching X – axis at a distance 3 from the origin and having an intercept of length on Y – axis is/are a) x2 + y2 – 6x + 8y + 9 = 0 b) x2 + y2 – 6x + 7y + 9 = 0 c) x2 + y2 – 6x − 8y + 9 = 0 d) x2 + y2 – 6x − 7y + 9 = 0
|
IIT 2013 |
|
|
1046 |
Using induction or otherwise, prove that for any non-negative integers m, n, r and k
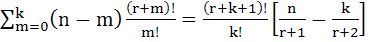
Using induction or otherwise, prove that for any non-negative integers m, n, r and k
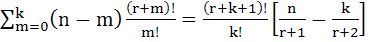
|
IIT 1991 |
|
|
1047 |
Let V be the volume of the parallelepiped formed by the vectors 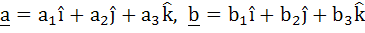 and and 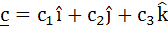 . If ar, br, cr where r = 1, 2, 3 are non-negative real numbers and . If ar, br, cr where r = 1, 2, 3 are non-negative real numbers and 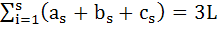 , show that V ≤ L3 , show that V ≤ L3
|
IIT 2002 |
|
|
1048 |
One or more than one correct option A circle S passes through the point (0, 1) and is orthogonal to the circles (x – 1)2 + y2 = 16 and x2 + y2 = 1, then a) Radius of S is 8 b) Radius of S is 7 c) Centre of S is (−7, 1) d) Centre of S is (−8, 1)
One or more than one correct option A circle S passes through the point (0, 1) and is orthogonal to the circles (x – 1)2 + y2 = 16 and x2 + y2 = 1, then a) Radius of S is 8 b) Radius of S is 7 c) Centre of S is (−7, 1) d) Centre of S is (−8, 1)
|
IIT 2014 |
|
|
1049 |
The locus of the midpoint of a chord of the circle 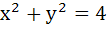 which subtend a right angle at the origin is which subtend a right angle at the origin is a) 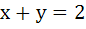 b) 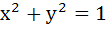 c) 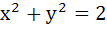 d) 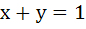
The locus of the midpoint of a chord of the circle 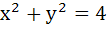 which subtend a right angle at the origin is which subtend a right angle at the origin is a) 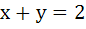 b) 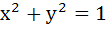 c) 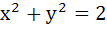 d) 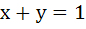
|
IIT 1984 |
|
|
1050 |
If n is a positive integer and 0 ≤ v < π then show that 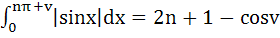
If n is a positive integer and 0 ≤ v < π then show that 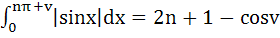
|
IIT 1994 |
|