Let f(x) =  where p is a constant

Then  at x = 0 is

a) p

b)

c)

d) Independent of p

If y is a function of x and ln (x + y) – 2xy = 0 then the value of

y’ (0) is equal to

a) 1

b) – 1

c) 2

d) 0

If y = y (x) and it follows the relation xcosy + ycosx = π then  is

a) – 1

b) π

c) – π

d) 1

 equals

a)

b)

c)

d)

If f (x) = , find  from first principle.

a)

b)

c)

d)

Given  find

Let y =  Find

a)

b)

c)

d) 0

If y =  

Prove that  

The derivative of an even function is always an odd function.

a) False

b) True

If and , then find  

If  then  at x = e is .  .  .

a) 0

b)

c) e

d) 1

The derivative of  with respect to  at x =  is

a) 0

b) 1

c) 2

d) 4

If f (x) = |x – 2| and g (x) =  then  for x > 20

a) 0

b) 1

c) 2

d) 4

If  then at x = 0,  is equal to

a) 0

b) 1

c) 2

d) 4

Let F(x) = f (x) g (x) h (x) for all real x, where f (x), g (x) and h (x) are differentiable functions. At some point x₀

 and

 then k is equal to

a) 12

b) 20

c) 24

d) 28

For a real y, let [y] denote the greatest integer less than or equal to y. Then the function 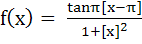 is

a) Discontinuous at some x

b) Continuous at all x but the derivative 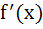 does not exist for some x

c) 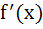 exists for all x but the derivative  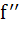does not exist for some x

d) 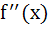 exists for all x

If G(x) then  is

a)

b)

c)

d)

If f (a) =  then the value of  is

a) – 5

b)

c) 5

d) None of these

 is equal to

a) 0

b)

c)

d) None of these

If

Where [x] denotes the greatest integer less than or equal to x then  equals

a) 1

b) 0

c) – 1

d) None of these

The set of all points where the function  is differentiable is

a)

b) [0, ∞)

c)  

d)  (0, ∞)

e)  None of these

The value of  is   

a) 1

b) – 1

c) 0

d) None of these

Let [.] denotes the greatest integer function and

f(x) =  then

a)  does not exist

b) f (x) is continuous at x = 0

c) f (x) is not differentiable at x = 0

d)