|
201 |
Multiple choice question On the ellipse 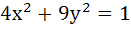 the points at which the tangents are parallel to the line the points at which the tangents are parallel to the line 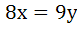 are are a) 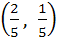 b) 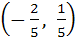 c) 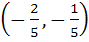 d) 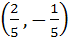
Multiple choice question On the ellipse 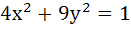 the points at which the tangents are parallel to the line the points at which the tangents are parallel to the line 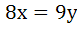 are are a) 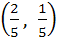 b) 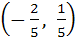 c) 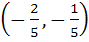 d) 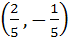
|
IIT 1999 |
03:37 min
|
|
202 |
The equation 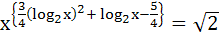 has has a) At least one real solution b) Exactly three real solutions c) Has exactly one irrational solution d) Complex roots
The equation 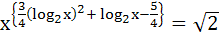 has has a) At least one real solution b) Exactly three real solutions c) Has exactly one irrational solution d) Complex roots
|
IIT 1989 |
03:53 min
|
|
203 |
Show that for for any triangle with sides a, b, c
3 (ab + bc + ac) ≤ (a + b + c)2 < 4 (ab + bc + ca)
Show that for for any triangle with sides a, b, c
3 (ab + bc + ac) ≤ (a + b + c)2 < 4 (ab + bc + ca)
|
IIT 1979 |
03:38 min
|
|
204 |
The solution set of equation 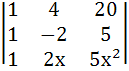 = 0 is ………. = 0 is ………. a) {0} b) {1, 2} c) {−1, 2} d) {−1, −2}
The solution set of equation 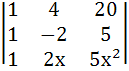 = 0 is ………. = 0 is ………. a) {0} b) {1, 2} c) {−1, 2} d) {−1, −2}
|
IIT 1981 |
02:12 min
|
|
205 |
An ellipse has eccentricity  and one of the focus at the point and one of the focus at the point 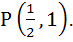 It’s one directrix is the common tangent near to the point P to the circle It’s one directrix is the common tangent near to the point P to the circle 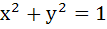 and the hyperbola and the hyperbola 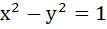 . Then the equation of the ellipse in the statement form is . . . . . . Then the equation of the ellipse in the statement form is . . . . .
|
IIT 1996 |
07:07 min
|
|
206 |
The equation 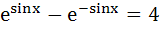 has has a) no real solutions b) one real solution c) two real solutions d) infinite real solutions
The equation 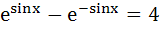 has has a) no real solutions b) one real solution c) two real solutions d) infinite real solutions
|
IIT 1982 |
03:09 min
|
|
207 |
For positive numbers x, y and z the numerical value of the determinant
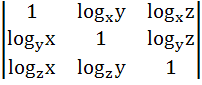 is ……….. is ……….. a) 1 b) –1 c) ±1 d) 0
For positive numbers x, y and z the numerical value of the determinant
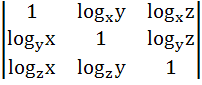 is ……….. is ……….. a) 1 b) –1 c) ±1 d) 0
|
IIT 1993 |
02:04 min
|
|
208 |
The equation 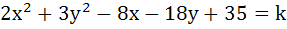 represents represents a) No locus if k > 0 b) An ellipse if k < 0 c) A point if k = 0 d) A hyperbola if k > 0
The equation 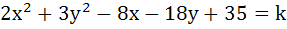 represents represents a) No locus if k > 0 b) An ellipse if k < 0 c) A point if k = 0 d) A hyperbola if k > 0
|
IIT 1994 |
02:16 min
|
|
209 |
If a > 0, b > 0, c > 0, prove that 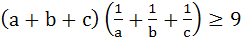
If a > 0, b > 0, c > 0, prove that 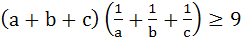
|
IIT 1984 |
02:45 min
|
|
210 |
The third term of Geometric Progression is 4. The product of the five terms is a) 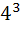 b) 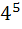 c) 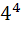 d) 
The third term of Geometric Progression is 4. The product of the five terms is a) 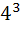 b) 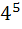 c) 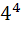 d) 
|
IIT 1982 |
01:07 min
|
|
211 |
If the line 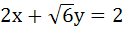 touches the hyperbola touches the hyperbola 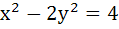 then the point of contact is then the point of contact is a) 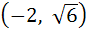 b) 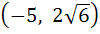 c) 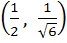 d) 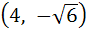
If the line 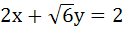 touches the hyperbola touches the hyperbola 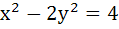 then the point of contact is then the point of contact is a) 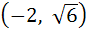 b) 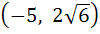 c) 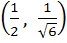 d) 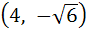
|
IIT 2004 |
02:39 min
|
|
212 |
Let 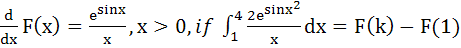 then one of the possible value of k is then one of the possible value of k is a) 1 b) 2 c) 4 d) 16
Let 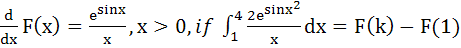 then one of the possible value of k is then one of the possible value of k is a) 1 b) 2 c) 4 d) 16
|
IIT 1997 |
02:15 min
|
|
213 |
Two events A and B have probabilities 0.25 and 0.50 respectively. The possibility of both A and B occur simultaneously is 0.14 then the probability that neither A nor B occur is a) 0.39 b) 0.25 c) 0.11 d) None of these
Two events A and B have probabilities 0.25 and 0.50 respectively. The possibility of both A and B occur simultaneously is 0.14 then the probability that neither A nor B occur is a) 0.39 b) 0.25 c) 0.11 d) None of these
|
IIT 1980 |
02:08 min
|
|
214 |
Find the set of all x for which 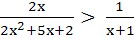
Find the set of all x for which 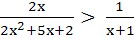
|
IIT 1987 |
05:05 min
|
|
215 |
Sum of the first n terms of the series 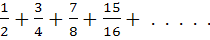 is is a) 2n – n – 1 b) 1 – 2− n c) n + 2− n – 1 d) 2n + 1
Sum of the first n terms of the series 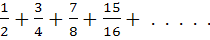 is is a) 2n – n – 1 b) 1 – 2− n c) n + 2− n – 1 d) 2n + 1
|
IIT 1988 |
03:20 min
|
|
216 |
The value of the integral
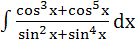 is is a) sin−1 x – 6tan−1(sin−1 x) + c b) sin−1x – 2(sinx)−1 + c c) sin−1x – 2(sinx)−1 − 6tan−1(sin−1x) + c d) sin−1x – 2(sinx)−1 + 5tan−1(sin−1x) + c
The value of the integral
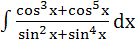 is is a) sin−1 x – 6tan−1(sin−1 x) + c b) sin−1x – 2(sinx)−1 + c c) sin−1x – 2(sinx)−1 − 6tan−1(sin−1x) + c d) sin−1x – 2(sinx)−1 + 5tan−1(sin−1x) + c
|
IIT 1995 |
07:00 min
|
|
217 |
Three identical dice are rolled. The probability that the same number will appear on each of them is a)  b) 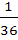 c) 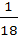 d) 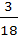
Three identical dice are rolled. The probability that the same number will appear on each of them is a)  b) 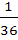 c) 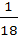 d) 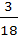
|
IIT 1984 |
01:22 min
|
|
218 |
Let 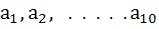 be in Arithmetic Progression and be in Arithmetic Progression and
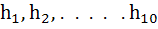 be in Harmonic Progression. If be in Harmonic Progression. If 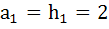 and and
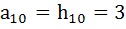 then then 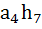 is is a) 2 b) 3 c) 5 d) 6
Let 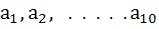 be in Arithmetic Progression and be in Arithmetic Progression and
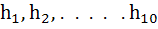 be in Harmonic Progression. If be in Harmonic Progression. If 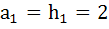 and and
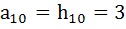 then then 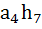 is is a) 2 b) 3 c) 5 d) 6
|
IIT 1999 |
04:53 min
|
|
219 |
Integrate 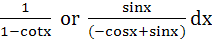 a) 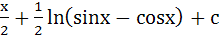 b) 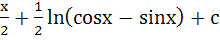 c) 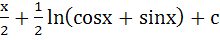 d) 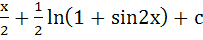
|
IIT 1978 |
04:43 min
|
|
220 |
An unbiased die with faces marked 1, 2, 3, 4, 5 and 6 is rolled 4 times. Out of four face values obtained, the probability that the minimum face value is not less than 2 and the maximum face value is not greater than 5 is a) 16/81 b) 1/81 c) 80/81 d) 65/81
An unbiased die with faces marked 1, 2, 3, 4, 5 and 6 is rolled 4 times. Out of four face values obtained, the probability that the minimum face value is not less than 2 and the maximum face value is not greater than 5 is a) 16/81 b) 1/81 c) 80/81 d) 65/81
|
IIT 1993 |
01:57 min
|
|
221 |
If α, β are roots of 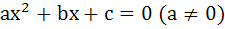 and and 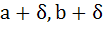 are roots of are roots of 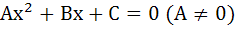 for some constant δ, then prove that for some constant δ, then prove that
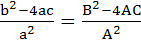
|
IIT 2000 |
03:16 min
|
|
222 |
Let the positive numbers a, b, c, d be in Arithmetic Progression. Then
abc, abd, acd, bcd are a) Not in Arithmetic Progression/Geometric Progression/Harmonic Progression b) In Arithmetic Progression c) In Geometric Progression d) In Harmonic Progression
Let the positive numbers a, b, c, d be in Arithmetic Progression. Then
abc, abd, acd, bcd are a) Not in Arithmetic Progression/Geometric Progression/Harmonic Progression b) In Arithmetic Progression c) In Geometric Progression d) In Harmonic Progression
|
IIT 2001 |
01:12 min
|
|
223 |
If f(x) be the interval of 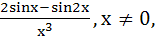 find find 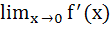 a) ½ b) 1 c) 2 d) 4
If f(x) be the interval of 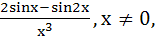 find find 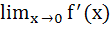 a) ½ b) 1 c) 2 d) 4
|
IIT 1979 |
01:57 min
|
|
224 |
For the three events A, B, C, P(exactly one of A or B occurs) = P(exactly one of B or C occurs) = P(exactly one of C or A occurs) = p and P(all the three events occur simultaneously = 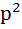 where where 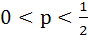 . Then the probability of at least one of A, B, C occurring is . Then the probability of at least one of A, B, C occurring is a) 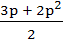 b) 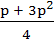 c) 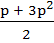 d) 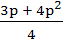
For the three events A, B, C, P(exactly one of A or B occurs) = P(exactly one of B or C occurs) = P(exactly one of C or A occurs) = p and P(all the three events occur simultaneously = 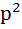 where where 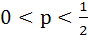 . Then the probability of at least one of A, B, C occurring is . Then the probability of at least one of A, B, C occurring is a) 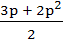 b) 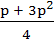 c) 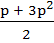 d) 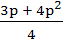
|
IIT 1996 |
06:23 min
|
|
225 |
If 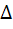 is the area of a triangle with sides a, b, c then show that is the area of a triangle with sides a, b, c then show that
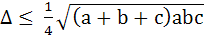 . .
Also show that equality occurs if a = b = c
If 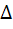 is the area of a triangle with sides a, b, c then show that is the area of a triangle with sides a, b, c then show that
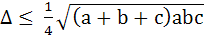 . .
Also show that equality occurs if a = b = c
|
IIT 2001 |
05:12 min
|