|
176 |
In the binomial expansion of 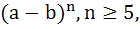 the sum of the 5th term and 6th term is zero, then the sum of the 5th term and 6th term is zero, then 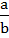 equals equals a) 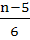 b) 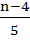 c) 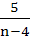 d) 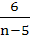
In the binomial expansion of 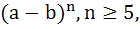 the sum of the 5th term and 6th term is zero, then the sum of the 5th term and 6th term is zero, then 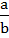 equals equals a) 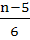 b) 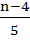 c) 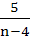 d) 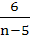
|
IIT 2001 |
02:04 min
|
|
177 |
Multiple choice Let a and b be two non-collinear unit vectors. If 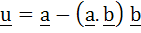 and and 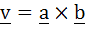 then then 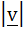 is is a) |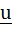 | | b) 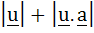 c) 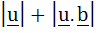 d) 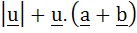
Multiple choice Let a and b be two non-collinear unit vectors. If 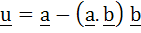 and and 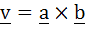 then then 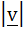 is is a) |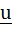 | | b) 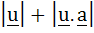 c) 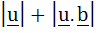 d) 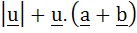
|
IIT 1999 |
03:32 min
|
|
178 |
Let F(x) = f (x) g (x) h (x) for all real x, where f (x), g (x) and h (x) are differentiable functions. At some point x0 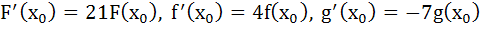 and and
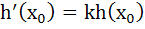 then k is equal to then k is equal to
a) 12 b) 20 c) 24 d) 28
Let F(x) = f (x) g (x) h (x) for all real x, where f (x), g (x) and h (x) are differentiable functions. At some point x0 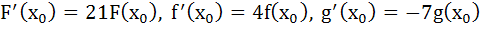 and and
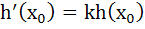 then k is equal to then k is equal to
a) 12 b) 20 c) 24 d) 28
|
IIT 1997 |
01:17 min
|
|
179 |
If 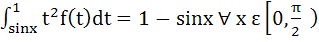 then f then f 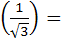 a) 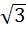 b)  c) 3 d) None
If 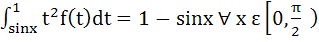 then f then f 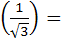 a) 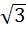 b)  c) 3 d) None
|
IIT 2005 |
02:29 min
|
|
180 |
If c be a given non-zero scalar and A and B be given non-zero vectors such that A is perpendicular to B, find the vector X which satisfies the equations 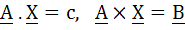
If c be a given non-zero scalar and A and B be given non-zero vectors such that A is perpendicular to B, find the vector X which satisfies the equations 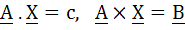
|
IIT 1983 |
01:16 min
|
|
181 |
The set of all values of x in the interval (0, π) for which
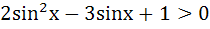 is is a) (0 , , 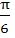 ) ) b) {  } } c) ( 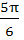 , π) , π) d) (0 , ,  ) U { ) U {  } U ( } U ( 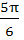 , π) , π)
|
IIT 1987 |
02:55 min
|
|
182 |
If G(x)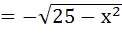 then then 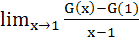 is is a) 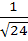 b)  c) 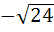 d) 
If G(x)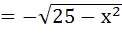 then then 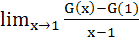 is is a) 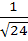 b)  c) 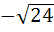 d) 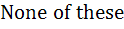
|
IIT 1983 |
01:40 min
|
|
183 |
Show that 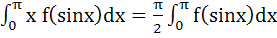
Show that 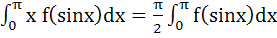
|
IIT 1982 |
01:38 min
|
|
184 |
If a, b, c are coplanar, show that
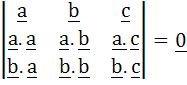
If a, b, c are coplanar, show that
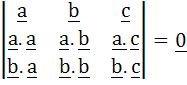
|
IIT 1989 |
02:38 min
|
|
185 |
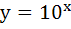 is the reflexion of is the reflexion of  in the line whose equation is . . in the line whose equation is . .
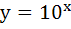 is the reflexion of is the reflexion of  in the line whose equation is . . in the line whose equation is . .
|
IIT 1982 |
00:57 min
|
|
186 |
Use mathematical induction to prove that 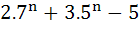 is divisible by 24 for all n > 0. is divisible by 24 for all n > 0.
Use mathematical induction to prove that 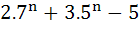 is divisible by 24 for all n > 0. is divisible by 24 for all n > 0.
|
IIT 1985 |
03:43 min
|
|
187 |
If 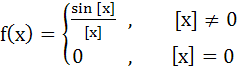 Where [x] denotes the greatest integer less than or equal to x then 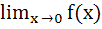 equals equals a) 1 b) 0 c) – 1 d) None of these
If 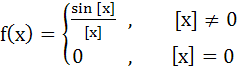 Where [x] denotes the greatest integer less than or equal to x then 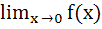 equals equals a) 1 b) 0 c) – 1 d) None of these
|
IIT 1985 |
02:39 min
|
|
188 |
Evaluate 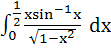 a)  b) 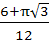 c) 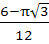 d) 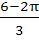
|
IIT 1984 |
03:38 min
|
|
189 |
Given the points A (0, 4) and B (0, - 4) the equation of the locus of the point P (x, y) such that |AP – BP| = 6 is . . . . .
Given the points A (0, 4) and B (0, - 4) the equation of the locus of the point P (x, y) such that |AP – BP| = 6 is . . . . .
|
IIT 1983 |
05:23 min
|
|
190 |
The solution of 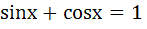 is is a) 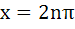 b) 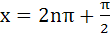 c) 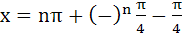 d) None of these
The solution of 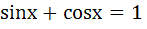 is is a) 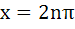 b) 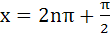 c) 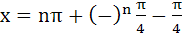 d) None of these
|
IIT 1981 |
01:11 min
|
|
191 |
Let [.] denotes the greatest integer function and f(x) = 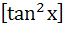 then then a) 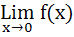 does not exist does not exist b) f (x) is continuous at x = 0 c) f (x) is not differentiable at x = 0 d) 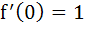
Let [.] denotes the greatest integer function and f(x) = 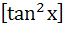 then then a) 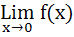 does not exist does not exist b) f (x) is continuous at x = 0 c) f (x) is not differentiable at x = 0 d) 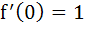
|
IIT 1993 |
01:28 min
|
|
192 |
Evaluate 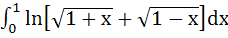 a) 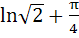 b) 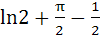 c) 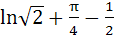 d) 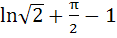
|
IIT 1988 |
06:04 min
|
|
193 |
Two circles 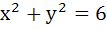 and and 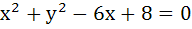 are given. Then the equation of the circle through their points of intersection and the point (1, 1) is are given. Then the equation of the circle through their points of intersection and the point (1, 1) is a) 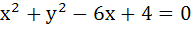 b) 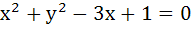 c) 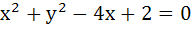 d) None of these
Two circles 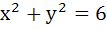 and and 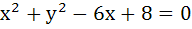 are given. Then the equation of the circle through their points of intersection and the point (1, 1) is are given. Then the equation of the circle through their points of intersection and the point (1, 1) is a) 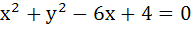 b) 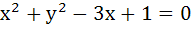 c) 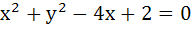 d) None of these
|
IIT 1980 |
02:25 min
|
|
194 |
If n be a positive integer such that
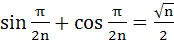 then then a) 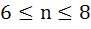 b) 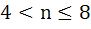 c) 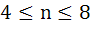 d) 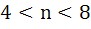
If n be a positive integer such that
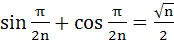 then then a) 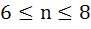 b) 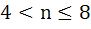 c) 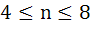 d) 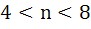
|
IIT 1994 |
03:42 min
|
|
195 |
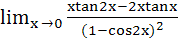 is is
a) 2 b) – 2 c)  d) 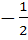
|
IIT 1999 |
03:16 min
|
|
196 |
Evaluate 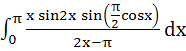 a)  b) 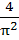 c) 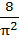 d) 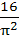
|
IIT 1991 |
09:59 min
|
|
197 |
Which of the following are rational? a) 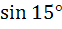 b) 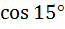 c) 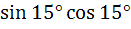 d) 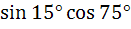
Which of the following are rational? a) 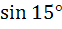 b) 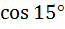 c) 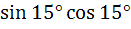 d) 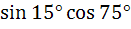
|
IIT 1998 |
02:53 min
|
|
198 |
Using mathematical induction prove that
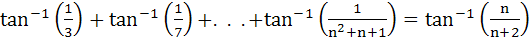
Using mathematical induction prove that
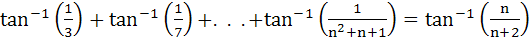
|
IIT 1993 |
08:39 min
|
|
199 |
For x ε R, 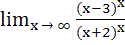 is equal to is equal to a) e b) 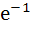 c) 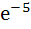 d) 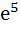
For x ε R, 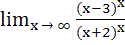 is equal to is equal to a) e b) 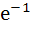 c) 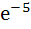 d) 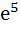
|
IIT 2000 |
06:08 min
|
|
200 |
Find the centre of the circle passing through (0, 0) and (1, 0) and touching the circle 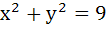 . .
Find the centre of the circle passing through (0, 0) and (1, 0) and touching the circle 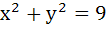 . .
|
IIT 1992 |
06:33 min
|