|
126 |
Multiple choices The function 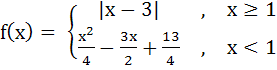 a) continuous at x = 1 b) differentiable at x = 1 c) continuous at x = 3 d) differentiable at x = 3
Multiple choices The function 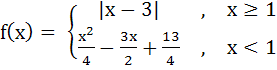 a) continuous at x = 1 b) differentiable at x = 1 c) continuous at x = 3 d) differentiable at x = 3
|
IIT 1988 |
04:52 min
|
|
127 |
The value of 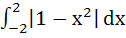 is is a) 0 b) 1 c) 2 d) 4
The value of 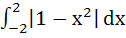 is is a) 0 b) 1 c) 2 d) 4
|
IIT 1989 |
03:14 min
|
|
128 |
If b and c are any two non-collinear unit vectors and a is any vector then 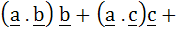 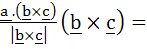 . . . . . . . . . .
If b and c are any two non-collinear unit vectors and a is any vector then 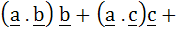 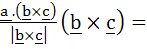 . . . . . . . . . .
|
IIT 1996 |
03:25 min
|
|
129 |
Tangent to the curve 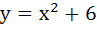 at the point P(1, 7) touches the circle at the point P(1, 7) touches the circle 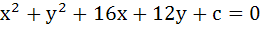 at a point Q then the coordinates of Q are at a point Q then the coordinates of Q are a) 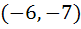 b) 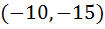 c) 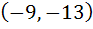 d) 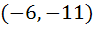
Tangent to the curve 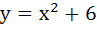 at the point P(1, 7) touches the circle at the point P(1, 7) touches the circle 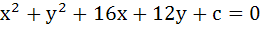 at a point Q then the coordinates of Q are at a point Q then the coordinates of Q are a) 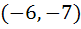 b) 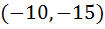 c) 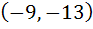 d) 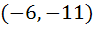
|
IIT 2005 |
05:15 min
|
|
130 |
For n > 0, 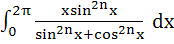 is is a)  b) π c) 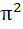 d) 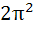
For n > 0, 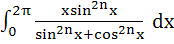 is is a)  b) π c) 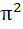 d) 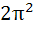
|
IIT 1996 |
08:23 min
|
|
131 |
The value of the definite integral 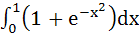 is is a) – 1 b) 2 c) 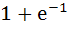 d) 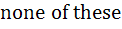
The value of the definite integral 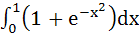 is is a) – 1 b) 2 c) 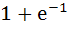 d) 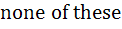
|
IIT 1981 |
02:44 min
|
|
132 |
Let A be the centre of the circle 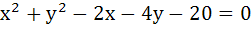 . Suppose the tangents at the points B (1, 7) and D (4, . Suppose the tangents at the points B (1, 7) and D (4,  2) on the circle meet at the point C, find the area of the quadrilateral ABCD. 2) on the circle meet at the point C, find the area of the quadrilateral ABCD.
Let A be the centre of the circle 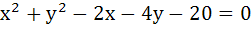 . Suppose the tangents at the points B (1, 7) and D (4, . Suppose the tangents at the points B (1, 7) and D (4,  2) on the circle meet at the point C, find the area of the quadrilateral ABCD. 2) on the circle meet at the point C, find the area of the quadrilateral ABCD.
|
IIT 1981 |
06:52 min
|
|
133 |
Find all the values of θ in the interval 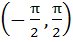 satisfying the equation satisfying the equation 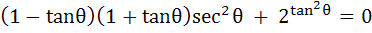 . . a)  b) 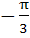 c) 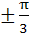 d) 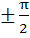
Find all the values of θ in the interval 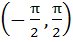 satisfying the equation satisfying the equation 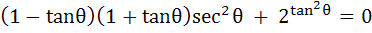 . . a)  b) 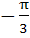 c) 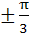 d) 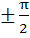
|
IIT 1996 |
01:41 min
|
|
134 |
If f (x) = 3x – 5 then f -1 (x) a) is given by 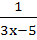 b) is given by 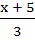 c) 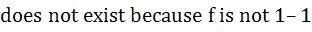 d) 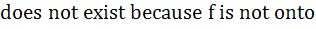
If f (x) = 3x – 5 then f -1 (x) a) is given by 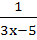 b) is given by 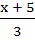 c) 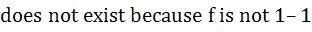 d) 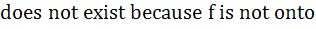
|
IIT 1998 |
01:38 min
|
|
135 |
Evaluate 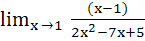 a) 0 b) 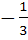 c)  d) 1
|
IIT 1978 |
01:06 min
|
|
136 |
If 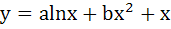 has its extremum value at x = has its extremum value at x = 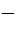 1 and x = 2, then 1 and x = 2, then a) a = 2, b = 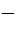 1 1 b) a = 2, 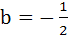 c) a = 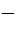 2, 2, 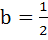 d) None of these
If 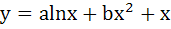 has its extremum value at x = has its extremum value at x = 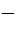 1 and x = 2, then 1 and x = 2, then a) a = 2, b = 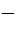 1 1 b) a = 2, 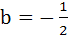 c) a = 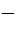 2, 2, 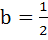 d) None of these
|
IIT 1983 |
02:13 min
|
|
137 |
Lines 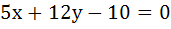 and and 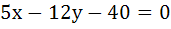 touch a circle C1 of diameter 6. If the centre of C1 lies in the first quadrant, find the equation of the circle C2 which is concentric with C1 and cuts intercepts of length 8 on these lines. touch a circle C1 of diameter 6. If the centre of C1 lies in the first quadrant, find the equation of the circle C2 which is concentric with C1 and cuts intercepts of length 8 on these lines.
Lines 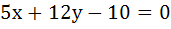 and and 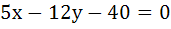 touch a circle C1 of diameter 6. If the centre of C1 lies in the first quadrant, find the equation of the circle C2 which is concentric with C1 and cuts intercepts of length 8 on these lines. touch a circle C1 of diameter 6. If the centre of C1 lies in the first quadrant, find the equation of the circle C2 which is concentric with C1 and cuts intercepts of length 8 on these lines.
|
IIT 1986 |
07:04 min
|
|
138 |
The solution set of the equations  where x and y are real is …………. where x and y are real is …………. a) 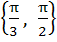 b) 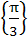 c) 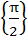 d) No solution
The solution set of the equations  where x and y are real is …………. where x and y are real is …………. a) 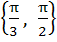 b) 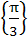 c) 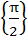 d) No solution
|
IIT 1986 |
02:21 min
|
|
139 |
If f (θ) = sinθ (sinθ + sin3θ) then f (θ) a) ≥ 0 only when θ ≥ 0 b) ≤ 0 for all real θ c) ≥ 0 for all real θ d) ≤ θ only when θ ≤ 0
If f (θ) = sinθ (sinθ + sin3θ) then f (θ) a) ≥ 0 only when θ ≥ 0 b) ≤ 0 for all real θ c) ≥ 0 for all real θ d) ≤ θ only when θ ≤ 0
|
IIT 2000 |
01:05 min
|
|
140 |
Evaluate 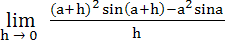 a) 2asina b) a2cosa c) 2asina + a2cosa d) 2a
Evaluate 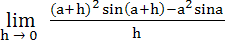 a) 2asina b) a2cosa c) 2asina + a2cosa d) 2a
|
IIT 1980 |
01:38 min
|
|
141 |
For 2 ≤ r ≤ n, 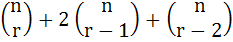 is equal to is equal to a) 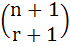 b) 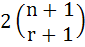 c) 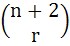 d) 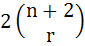
For 2 ≤ r ≤ n, 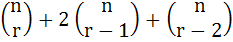 is equal to is equal to a) 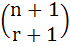 b) 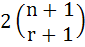 c) 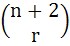 d) 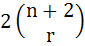
|
IIT 2000 |
03:00 min
|
|
142 |
Which of the following curves cut the parabola 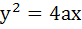 at right angles? at right angles? a) 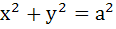 b) 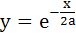 c) 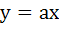 d) 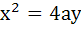
Which of the following curves cut the parabola 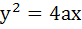 at right angles? at right angles? a) 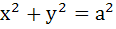 b) 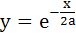 c) 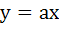 d) 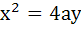
|
IIT 1994 |
02:31 min
|
|
143 |
If 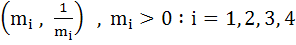 are four points on a circle then show that are four points on a circle then show that 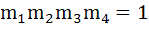 . .
If 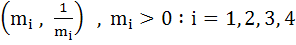 are four points on a circle then show that are four points on a circle then show that 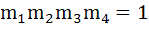 . .
|
IIT 1989 |
01:43 min
|
|
144 |
The value of 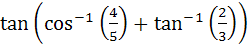 is is a) 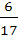 b) 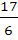 c) 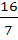 d) None of these
The value of 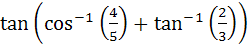 is is a) 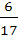 b) 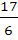 c) 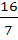 d) None of these
|
IIT 1983 |
02:14 min
|
|
145 |
The domain of f (x) = 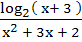 is is a) R – {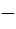 1, 1, 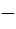 2} 2} b) (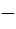 2, 2, 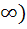 c) R – { 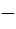 1, 1, 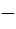 2, 2, 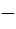 3} 3} d) (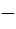 3, 3, 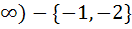
|
IIT 2001 |
01:19 min
|
|
146 |
Let 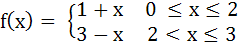 Determine the function g (x) = f (f(x)) and hence find the points of discontinuity of g if any. a) g(x) is continuous for all x except x = 1 and x = 2 b) g(x) is continuous for all x except x = 1 c) g(x) is continuous for all x except x = 2 d) g(x) is continuous for all x
Let 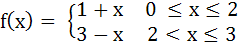 Determine the function g (x) = f (f(x)) and hence find the points of discontinuity of g if any. a) g(x) is continuous for all x except x = 1 and x = 2 b) g(x) is continuous for all x except x = 1 c) g(x) is continuous for all x except x = 2 d) g(x) is continuous for all x
|
IIT 1983 |
05:15 min
|
|
147 |
The slope of the tangent to the curve y = f(x) at [x, f(x)] is 2x + 1. The curve passes through (1, 2), then the area bounded by the curve and X–axis, and the line x = 1 is a)  b)  c)  d) 6
The slope of the tangent to the curve y = f(x) at [x, f(x)] is 2x + 1. The curve passes through (1, 2), then the area bounded by the curve and X–axis, and the line x = 1 is a)  b)  c)  d) 6
|
IIT 1995 |
03:15 min
|
|
148 |
Three circles touch each other externally. The tangents at their points of contact meet at a point whose distance from a point of contact is 4. Find the ratio of the product of the radii to the sum of the radii of the circles.
Three circles touch each other externally. The tangents at their points of contact meet at a point whose distance from a point of contact is 4. Find the ratio of the product of the radii to the sum of the radii of the circles.
|
IIT 1992 |
07:55 min
|
|
149 |
The number of solutions of 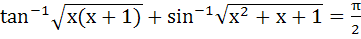 is is a) 0 b) One c) Two d) Infinite
The number of solutions of 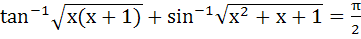 is is a) 0 b) One c) Two d) Infinite
|
IIT 2001 |
04:00 min
|
|
150 |
Let f (x) be a continuous function satisfying 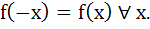 If If 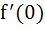 exists, find its value. exists, find its value. a) 0 b) 1 c) 2 d) 4
Let f (x) be a continuous function satisfying 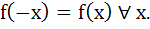 If If 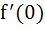 exists, find its value. exists, find its value. a) 0 b) 1 c) 2 d) 4
|
IIT 1987 |
03:18 min
|