|
1301 |
Find the values of a and b, so that the functions 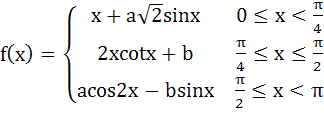
Is continuous for 0 ≤ x ≤ π a) 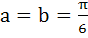 b) 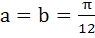 c) 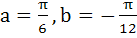 d) 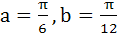
Find the values of a and b, so that the functions 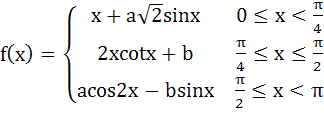
Is continuous for 0 ≤ x ≤ π a) 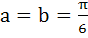 b) 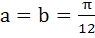 c) 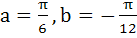 d) 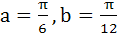
|
IIT 1989 |
|
|
1302 |
C1 and C2 are two concentric circles, the radius of C2 being twice of C1 . From a point on C2 tangents PA and PB are drawn to C1. Prove that the centroid of ΔPAB lies on C1.
C1 and C2 are two concentric circles, the radius of C2 being twice of C1 . From a point on C2 tangents PA and PB are drawn to C1. Prove that the centroid of ΔPAB lies on C1.
|
IIT 1998 |
|
|
1303 |
In [0, 1], Lagrange’s Mean Value theorem is not applicable to a) 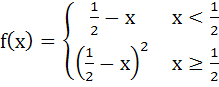 b) 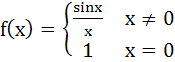 c) 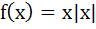 d) 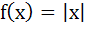
In [0, 1], Lagrange’s Mean Value theorem is not applicable to a) 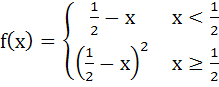 b) 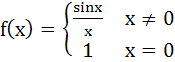 c) 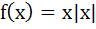 d) 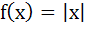
|
IIT 2003 |
|
|
1304 |
Let α ε ℝ, then a function f : ℝ → ℝ is differentiable at α if and only if there is a function g : ℝ → ℝ which is continuous at α and satisfies f(x) – f(α) = g(x) (x – α) for all x ε ℝ. a) True b) False
Let α ε ℝ, then a function f : ℝ → ℝ is differentiable at α if and only if there is a function g : ℝ → ℝ which is continuous at α and satisfies f(x) – f(α) = g(x) (x – α) for all x ε ℝ. a) True b) False
|
IIT 2001 |
|
|
1305 |
The area bounded by the angle bisectors of the lines x2 – y2 + 2y = 1 and the line x + y = 3 is a) 2 b) 3 c) 4 d) 6
The area bounded by the angle bisectors of the lines x2 – y2 + 2y = 1 and the line x + y = 3 is a) 2 b) 3 c) 4 d) 6
|
IIT 2004 |
|
|
1306 |
If two functions f and g satisfy the given conditions  x, y ε ℝ, f(x – y) = f(x)g(y) – f(y)g(x) and g(x – y) = g(x) . g(y) + f(x) . f(y). x, y ε ℝ, f(x – y) = f(x)g(y) – f(y)g(x) and g(x – y) = g(x) . g(y) + f(x) . f(y). If the RHD at x = 0 exists for f(x) then find the derivative of g(x) at x = 0.
If two functions f and g satisfy the given conditions  x, y ε ℝ, f(x – y) = f(x)g(y) – f(y)g(x) and g(x – y) = g(x) . g(y) + f(x) . f(y). x, y ε ℝ, f(x – y) = f(x)g(y) – f(y)g(x) and g(x – y) = g(x) . g(y) + f(x) . f(y). If the RHD at x = 0 exists for f(x) then find the derivative of g(x) at x = 0.
|
IIT 2005 |
|
|
1307 |
Let 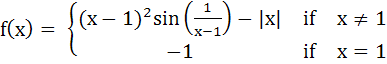 be a real valued function. The set of points where f(x) is not differentiable are a) {0} b) {1} c) {0, 1} d) {∅}
Let 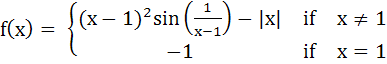 be a real valued function. The set of points where f(x) is not differentiable are a) {0} b) {1} c) {0, 1} d) {∅}
|
IIT 1981 |
|
|
1308 |
Multiple choice Let 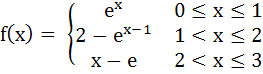 and and 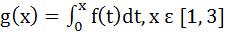
Then g(x) has a) Local maximum at x = 1 + ln2 and local minima at x = e b) Local maximum at x = 1 and local minima at x = 2 c) No local maximas d) No local minimas
Multiple choice Let 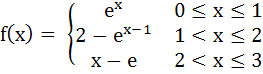 and and 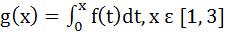
Then g(x) has a) Local maximum at x = 1 + ln2 and local minima at x = e b) Local maximum at x = 1 and local minima at x = 2 c) No local maximas d) No local minimas
|
IIT 2006 |
|
|
1309 |
For all x in [0, 1], let the second derivative 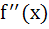 of a function f(x) exists and satisfies of a function f(x) exists and satisfies 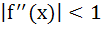 . If f(0) = f(1) then for all x ε [0, 1] . If f(0) = f(1) then for all x ε [0, 1] a) 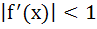 b) 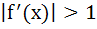 c) None of these
For all x in [0, 1], let the second derivative 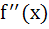 of a function f(x) exists and satisfies of a function f(x) exists and satisfies 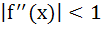 . If f(0) = f(1) then for all x ε [0, 1] . If f(0) = f(1) then for all x ε [0, 1] a) 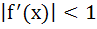 b) 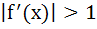 c) None of these
|
IIT 1981 |
|
|
1310 |
Match the following Let the function defined in column 1 have domain 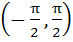 and range ( and range (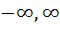 ) ) | Column 1 | Column 2 | | i) 1 + 2x | A) Onto but not one-one | | ii) tan x | B) One-one but not onto | | | C) One-one and onto | | | D) Neither one |
Match the following Let the function defined in column 1 have domain 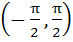 and range ( and range (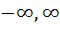 ) ) | Column 1 | Column 2 | | i) 1 + 2x | A) Onto but not one-one | | ii) tan x | B) One-one but not onto | | | C) One-one and onto | | | D) Neither one |
|
IIT 1992 |
|
|
1311 |
Let f(x) = [x]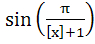 where [.] denotes the greatest integer function. Then the domain of f is . . . ., points of discontinuity of f are . . . . where [.] denotes the greatest integer function. Then the domain of f is . . . ., points of discontinuity of f are . . . . a) ∀ x ε I b) ∀ x ε I − {0} c) ∀ x ε I – {0, 1} d) ∀ x ε I – {0, 1, 2}
Let f(x) = [x]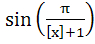 where [.] denotes the greatest integer function. Then the domain of f is . . . ., points of discontinuity of f are . . . . where [.] denotes the greatest integer function. Then the domain of f is . . . ., points of discontinuity of f are . . . . a) ∀ x ε I b) ∀ x ε I − {0} c) ∀ x ε I – {0, 1} d) ∀ x ε I – {0, 1, 2}
|
IIT 1996 |
|
|
1312 |
PQ and PR are two infinite rays, QAR is an arc.
Points lying in the shaded region excluding the boundary satisfies a) |z + 1| > 2; |arg(z + 1)| < 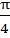 b) |z + 1| < 2; |arg(z + 1)| <  c) 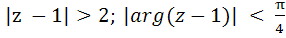 d) 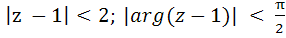
PQ and PR are two infinite rays, QAR is an arc. Points lying in the shaded region excluding the boundary satisfies a) |z + 1| > 2; |arg(z + 1)| < 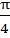 b) |z + 1| < 2; |arg(z + 1)| <  c) 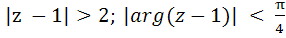 d) 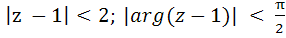
|
IIT 2005 |
|
|
1313 |
If 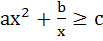 for all positive x where a > 0 and b > 0 then for all positive x where a > 0 and b > 0 then a) 9ab2 ≥ 4c3 b) 27ab2 ≥ 4c3 c) 9ab2 ≤ 4c3 d) 27ab2 ≤ 4c3
If 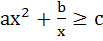 for all positive x where a > 0 and b > 0 then for all positive x where a > 0 and b > 0 then a) 9ab2 ≥ 4c3 b) 27ab2 ≥ 4c3 c) 9ab2 ≤ 4c3 d) 27ab2 ≤ 4c3
|
IIT 1989 |
|
|
1314 |
Let ABCD be a square with side of length 2 units. C2 is the circle through the vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A. If P is a point on C1 and Q is another point on C2, then 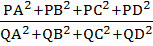 is equal to is equal to a) 0.75 b) 1.25 c) 1 d) 0.5
Let ABCD be a square with side of length 2 units. C2 is the circle through the vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A. If P is a point on C1 and Q is another point on C2, then 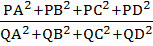 is equal to is equal to a) 0.75 b) 1.25 c) 1 d) 0.5
|
IIT 2006 |
|
|
1315 |
If a continuous function f defined on the real line ℝ, assumes positive and negative values in ℝ then the equation f(x) = 0 has a root in ℝ. For example, it is known that if a continuous function f on ℝ is positive at some points and its minimum value is negative then the equation f(x) = 0 has a root in ℝ. Consider the function f(x) = 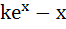 for all real x where k is a real constant. for all real x where k is a real constant. The positive value of k for which 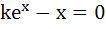 has only one root is has only one root is a)  b) 1 c) e d) ln2
If a continuous function f defined on the real line ℝ, assumes positive and negative values in ℝ then the equation f(x) = 0 has a root in ℝ. For example, it is known that if a continuous function f on ℝ is positive at some points and its minimum value is negative then the equation f(x) = 0 has a root in ℝ. Consider the function f(x) = 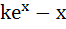 for all real x where k is a real constant. for all real x where k is a real constant. The positive value of k for which 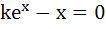 has only one root is has only one root is a)  b) 1 c) e d) ln2
|
IIT 2007 |
|
|
1316 |
Let 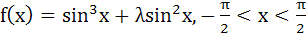 . Find the intervals in which λ should lie in order that f(x) has exactly one minimum and exactly one maximum. . Find the intervals in which λ should lie in order that f(x) has exactly one minimum and exactly one maximum. a) 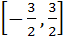 b) 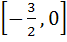 c) 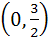 d) 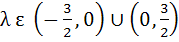
Let 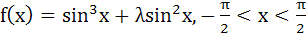 . Find the intervals in which λ should lie in order that f(x) has exactly one minimum and exactly one maximum. . Find the intervals in which λ should lie in order that f(x) has exactly one minimum and exactly one maximum. a) 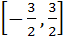 b) 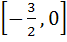 c) 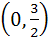 d) 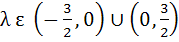
|
IIT 1985 |
|
|
1317 |
Consider a circle with centre lying on the focus of the parabola 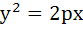 such that it touches the directrix of the parabola. Then a point of intersection of the circle and parabola is such that it touches the directrix of the parabola. Then a point of intersection of the circle and parabola is a) 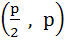 or or 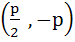 b) 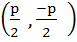 c) 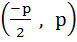 d) 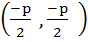
Consider a circle with centre lying on the focus of the parabola 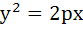 such that it touches the directrix of the parabola. Then a point of intersection of the circle and parabola is such that it touches the directrix of the parabola. Then a point of intersection of the circle and parabola is a) 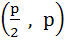 or or 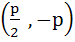 b) 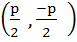 c) 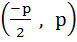 d) 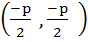
|
IIT 1995 |
|
|
1318 |
Find the equation of the plane at a distance 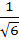 from the point from the point 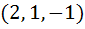 and containing the line and containing the line
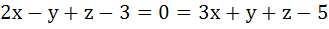 . .
|
IIT 2005 |
|
|
1319 |
Let the complex numbers 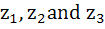 are vertices of an equilateral triangle. If are vertices of an equilateral triangle. If 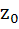 be the circumcentre of the triangle, then prove that be the circumcentre of the triangle, then prove that 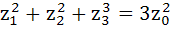
|
IIT 1981 |
|
|
1320 |
A two metre long object is fired vertically upwards from the mid-point of two locations A and B, 8 metres apart. The speed of the object after t seconds is given by 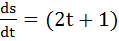 metres per second. Let α and β be the angles subtended by the objects A and B respectively after one and two seconds. Find the value of cos(α − β). metres per second. Let α and β be the angles subtended by the objects A and B respectively after one and two seconds. Find the value of cos(α − β). a) 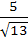 b) 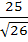 c) 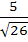 d) 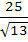
A two metre long object is fired vertically upwards from the mid-point of two locations A and B, 8 metres apart. The speed of the object after t seconds is given by 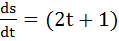 metres per second. Let α and β be the angles subtended by the objects A and B respectively after one and two seconds. Find the value of cos(α − β). metres per second. Let α and β be the angles subtended by the objects A and B respectively after one and two seconds. Find the value of cos(α − β). a) 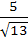 b) 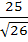 c) 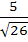 d) 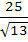
|
IIT 1989 |
|
|
1321 |
The point (α, β, γ) lies on the plane 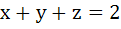 . .
Let a = 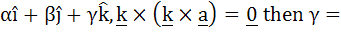 . . . . . . . . . .
The point (α, β, γ) lies on the plane 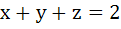 . .
Let a = 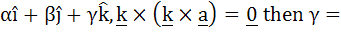 . . . . . . . . . .
|
IIT 2006 |
|
|
1322 |
Investigate for maxima and minima the function
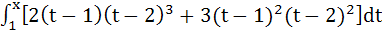 a) Local maximum at x = 1, 7/5, 2 b) Local minimum at x = 1, 7/5, 2 c) Local maximum at x = 1, 2. Local minimum at x = 7/5 d) Local maximum at x = 1. Local minimum at x = 7/5
Investigate for maxima and minima the function
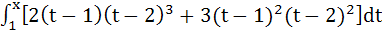 a) Local maximum at x = 1, 7/5, 2 b) Local minimum at x = 1, 7/5, 2 c) Local maximum at x = 1, 2. Local minimum at x = 7/5 d) Local maximum at x = 1. Local minimum at x = 7/5
|
IIT 1988 |
|
|
1323 |
Sides a, b, c of a triangle ABC are in arithmetic progression and 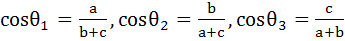 then then
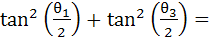
Sides a, b, c of a triangle ABC are in arithmetic progression and 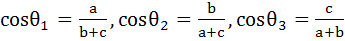 then then
|
IIT 2006 |
|
|
1324 |
A window of perimeter (including the base of the arch) is in the form of a rectangle surmounted by a semicircle. The semi-circular portion is fitted with coloured glass while the rectangular part is fitted with clear glass. The clear glass transmits three times as much light per square meter as the coloured glass. What is the ratio for the sides of the rectangle so that the window transmits the maximum light? a)  b)  c) 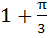 d) 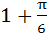
A window of perimeter (including the base of the arch) is in the form of a rectangle surmounted by a semicircle. The semi-circular portion is fitted with coloured glass while the rectangular part is fitted with clear glass. The clear glass transmits three times as much light per square meter as the coloured glass. What is the ratio for the sides of the rectangle so that the window transmits the maximum light? a)  b)  c) 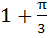 d) 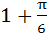
|
IIT 1991 |
|
|
1325 |
Let 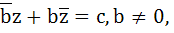 be a line in the complex plane where be a line in the complex plane where 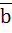 is the complex conjugate of b. If a point is the complex conjugate of b. If a point 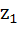 is the deflection of a point is the deflection of a point 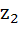 through the line, show that through the line, show that 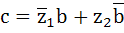 . .
|
IIT 1997 |
|