|
1276 |
For a positive integer n, define
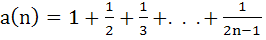 then then a) a(100) ≤ 100 b) a(100) > 100 c) a(200) ≤ 100 d) a(200) > 100
For a positive integer n, define
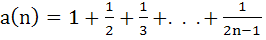 then then a) a(100) ≤ 100 b) a(100) > 100 c) a(200) ≤ 100 d) a(200) > 100
|
IIT 1999 |
|
|
1277 |
Let f:[0, 1] → ℝ (the set all real numbers)be a function. Suppose the function is twice differentiable, f(0) = f(1) = 0 and satisfiesf′′(x) – 2f′(x) + f(x) ≥ ex, x ∈ [0, 1]If the function e−x f(x) assumes its minimum in the interval [0, 1] at then which of the following is true? a) b) c) d)
Let f:[0, 1] → ℝ (the set all real numbers)be a function. Suppose the function is twice differentiable, f(0) = f(1) = 0 and satisfiesf′′(x) – 2f′(x) + f(x) ≥ ex, x ∈ [0, 1]If the function e−x f(x) assumes its minimum in the interval [0, 1] at then which of the following is true? a) b) c) d)
|
IIT 2013 |
|
|
1278 |
There exists a function f(x) satisfying f (0) = 1, 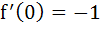 and and f (x) > 0 for all x and a) 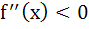 for all x for all x b) 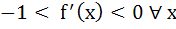 c) 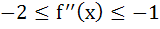 for all x for all x d) 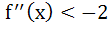 for all x for all x
There exists a function f(x) satisfying f (0) = 1, 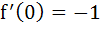 and and f (x) > 0 for all x and a) 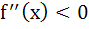 for all x for all x b) 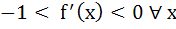 c) 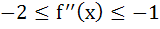 for all x for all x d) 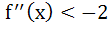 for all x for all x
|
IIT 1982 |
|
|
1279 |
Let k be an integer such that the triangle with vertices (k, −3k), (5, k) and (−k, 2) has area 28 square units. Then the orthocentre of the triangle is at the point a) b) c) d)
Let k be an integer such that the triangle with vertices (k, −3k), (5, k) and (−k, 2) has area 28 square units. Then the orthocentre of the triangle is at the point a) b) c) d)
|
IIT 2017 |
|
|
1280 |
If p is a natural number then prove that pn + 1 + (p + 1)2n – 1 is divisible by p2 + p + 1 for every positive integer n.
If p is a natural number then prove that pn + 1 + (p + 1)2n – 1 is divisible by p2 + p + 1 for every positive integer n.
|
IIT 1984 |
|
|
1281 |
A straight line L through the point (3, −2) is inclined at an angle of 60° to the line . If the line L also intersects the X- axis then the equation of L is a) b) c) d)
A straight line L through the point (3, −2) is inclined at an angle of 60° to the line . If the line L also intersects the X- axis then the equation of L is a) b) c) d)
|
IIT 2011 |
|
|
1282 |
The orthocenter of the triangle formed by the lines
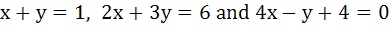 lies in the quadrant number . . . . . lies in the quadrant number . . . . .
The orthocenter of the triangle formed by the lines
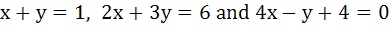 lies in the quadrant number . . . . . lies in the quadrant number . . . . .
|
IIT 1985 |
|
|
1283 |
Prove by mathematical induction that
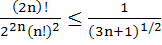 for every positive integer n. for every positive integer n.
Prove by mathematical induction that
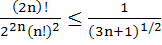 for every positive integer n. for every positive integer n.
|
IIT 1987 |
|
|
1284 |
The sides of a rhombus are along the lines x – y + 1 = 0 and 7x – y – 5 = 0. If its diagonals intersect at (−1, −2) then which one of the following is a vertex of the rhombus? a) b) c) d)
The sides of a rhombus are along the lines x – y + 1 = 0 and 7x – y – 5 = 0. If its diagonals intersect at (−1, −2) then which one of the following is a vertex of the rhombus? a) b) c) d)
|
IIT 2016 |
|
|
1285 |
Let 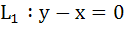 and and 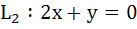 intersect the line intersect the line
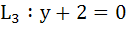 at P and Q respectively. Bisector of the acute angle between L1 and L2 intersects L3 in R. at P and Q respectively. Bisector of the acute angle between L1 and L2 intersects L3 in R.
Statement 1 – The ratio PR : RQ equals 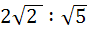 because because
Statement 2 – In any triangle, bisector of an angle divides the triangle into two similar triangles.
The question contains Statement 1(assertion) and Statement 2(reason). Of these statements, mark correct choice if a) Statement 1 and 2 are true. Statement 2 is a correct explanation for statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation for statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
Let 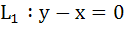 and and 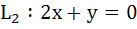 intersect the line intersect the line
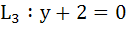 at P and Q respectively. Bisector of the acute angle between L1 and L2 intersects L3 in R. at P and Q respectively. Bisector of the acute angle between L1 and L2 intersects L3 in R.
Statement 1 – The ratio PR : RQ equals 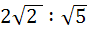 because because
Statement 2 – In any triangle, bisector of an angle divides the triangle into two similar triangles.
The question contains Statement 1(assertion) and Statement 2(reason). Of these statements, mark correct choice if a) Statement 1 and 2 are true. Statement 2 is a correct explanation for statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation for statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
|
IIT 2007 |
|
|
1286 |
Prove that 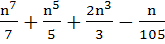 is an integer for every positive integer. is an integer for every positive integer.
Prove that 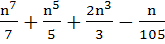 is an integer for every positive integer. is an integer for every positive integer.
|
IIT 1990 |
|
|
1287 |
If f is a continuous function with 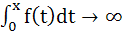 as |x| → ∞ then show that every line y = mx intersects the curve as |x| → ∞ then show that every line y = mx intersects the curve 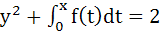 . .
If f is a continuous function with 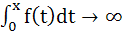 as |x| → ∞ then show that every line y = mx intersects the curve as |x| → ∞ then show that every line y = mx intersects the curve 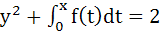 . .
|
IIT 1991 |
|
|
1288 |
Show, by vector method, that the angular bisectors of a triangle are concurrent and find an expression for the position vector of point of concurrency in terms of position vectors of the vertices.
Show, by vector method, that the angular bisectors of a triangle are concurrent and find an expression for the position vector of point of concurrency in terms of position vectors of the vertices.
|
IIT 2001 |
|
|
1289 |
The C be a circle with the centre at (1, 1) and radius 1. If T is the circle centred at (0, k) passing through origin and touches the circle C externally, then the radius of T is equal to a) b) c) d)
The C be a circle with the centre at (1, 1) and radius 1. If T is the circle centred at (0, k) passing through origin and touches the circle C externally, then the radius of T is equal to a) b) c) d)
|
IIT 2014 |
|
|
1290 |
If AB is a diameter of a circle and C is any point on the circumference of the circle then a) The area of ΔABC is maximum when it is isosceles b) The area of ΔABC is minimum when it is isosceles c) The perimeter of ΔABC is minimum when it is isosceles d) None of these
If AB is a diameter of a circle and C is any point on the circumference of the circle then a) The area of ΔABC is maximum when it is isosceles b) The area of ΔABC is minimum when it is isosceles c) The perimeter of ΔABC is minimum when it is isosceles d) None of these
|
IIT 1983 |
|
|
1291 |
Let f : ℝ → ℝ be any function. Define g : ℝ → ℝ by g (x) = |f (x)| for all x. Then g is a) Onto if f is onto b) One to one if f is one to one c) Continuous if f is continuous d) Differentiable if f is differentiable
Let f : ℝ → ℝ be any function. Define g : ℝ → ℝ by g (x) = |f (x)| for all x. Then g is a) Onto if f is onto b) One to one if f is one to one c) Continuous if f is continuous d) Differentiable if f is differentiable
|
IIT 2000 |
|
|
1292 |
Evaluate 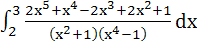 a) 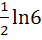 b) 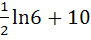 c) 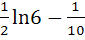 d) 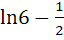
|
IIT 1993 |
|
|
1293 |
One or more than one correct option The circle C1 : x2 + y2 = 3 with centre at O intersect the parabola x2 = 2y at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2 and C3 at R2 and R3 respectively. Suppose C2 and C3 have equal radii and centres Q2 and Q3 respectively. If Q2 and Q3 lie on the Y- axis, then a) b) c) d)
One or more than one correct option The circle C1 : x2 + y2 = 3 with centre at O intersect the parabola x2 = 2y at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2 and C3 at R2 and R3 respectively. Suppose C2 and C3 have equal radii and centres Q2 and Q3 respectively. If Q2 and Q3 lie on the Y- axis, then a) b) c) d)
|
IIT 2016 |
|
|
1294 |
Let f : ℝ → ℝ be a function defined by f (x) = 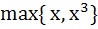 . The set of points where f (x) is not differentiable is . The set of points where f (x) is not differentiable is a) 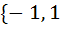 } } b) 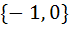 c) {0, 1} d) 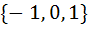
Let f : ℝ → ℝ be a function defined by f (x) = 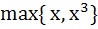 . The set of points where f (x) is not differentiable is . The set of points where f (x) is not differentiable is a) 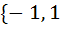 } } b) 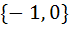 c) {0, 1} d) 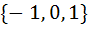
|
IIT 2001 |
|
|
1295 |
The circle passing through the point (−1, 0) and touching the Y – axis at (0, 2) also passes through the point a) b) c) d)
The circle passing through the point (−1, 0) and touching the Y – axis at (0, 2) also passes through the point a) b) c) d)
|
IIT 2011 |
|
|
1296 |
Let a, b, c be positive real numbers such that b2 – 4ac > 0 and let α1 = c. Prove by induction that
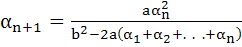 Is well defined and 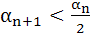 for n=1, 2, … for n=1, 2, … Here well defined means that the denominator in the expression of 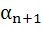 is not zero. is not zero.
Let a, b, c be positive real numbers such that b2 – 4ac > 0 and let α1 = c. Prove by induction that
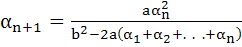 Is well defined and 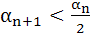 for n=1, 2, … for n=1, 2, … Here well defined means that the denominator in the expression of 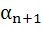 is not zero. is not zero.
|
IIT 2001 |
|
|
1297 |
Let O be the vertex and Q be any point on the parabola x2 = 8y. If the point P divides the line segment internally in the ratio 1 : 3 then the locus of P is a) x2 = y b) y2 = x c) y2 = 2x d) x2 = 2y
Let O be the vertex and Q be any point on the parabola x2 = 8y. If the point P divides the line segment internally in the ratio 1 : 3 then the locus of P is a) x2 = y b) y2 = x c) y2 = 2x d) x2 = 2y
|
IIT 2015 |
|
|
1298 |
Solve the following equation for x
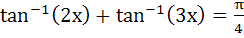 a) −1 b)  c) 0 d) −1 and 
Solve the following equation for x
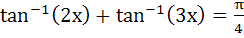 a) −1 b)  c) 0 d) −1 and 
|
IIT 1978 |
|
|
1299 |
If f is a differentiable function satisfying 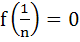 for all n ≥ 1, for all n ≥ 1, n 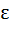 I then I then a) 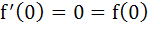 b) 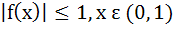 c) 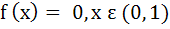 d) 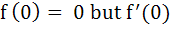 is not necessarily zero is not necessarily zero
If f is a differentiable function satisfying 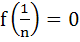 for all n ≥ 1, for all n ≥ 1, n 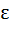 I then I then a) 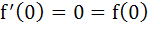 b) 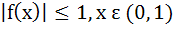 c) 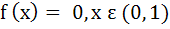 d) 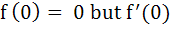 is not necessarily zero is not necessarily zero
|
IIT 2005 |
|
|
1300 |
Evaluate 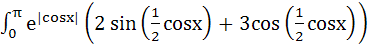
Evaluate 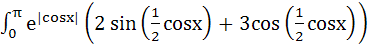
|
IIT 2005 |
|