|
1176 |
A tangent to the ellipse x2 + 4y2 = 4 meets the ellipse x2 + 2y2 = 6 at P and Q. Prove that tangents at P and Q of the ellipse x2 + 2y2 = 6 are at right angles.
A tangent to the ellipse x2 + 4y2 = 4 meets the ellipse x2 + 2y2 = 6 at P and Q. Prove that tangents at P and Q of the ellipse x2 + 2y2 = 6 are at right angles.
|
IIT 1997 |
|
|
1177 |
Let f(θ) = sinθ (sinθ + sin3θ) then f(θ) a) ≥ 0 only when θ ≥ 0 b) ≤ 0 for all real θ c) ≥ 0 for all real θ d) ≤ θ only when θ ≤ 0
Let f(θ) = sinθ (sinθ + sin3θ) then f(θ) a) ≥ 0 only when θ ≥ 0 b) ≤ 0 for all real θ c) ≥ 0 for all real θ d) ≤ θ only when θ ≤ 0
|
IIT 2000 |
|
|
1178 |
Let y = f(x) is a cubic polynomial having maximum at x = − 1 and 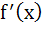 has a minimum at x = 1 and f(−1) = 10, f(1) = − 6. Find the cubic polynomial and also find the distance between the points which are maxima or minima. has a minimum at x = 1 and f(−1) = 10, f(1) = − 6. Find the cubic polynomial and also find the distance between the points which are maxima or minima. a) 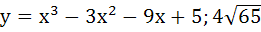 b) 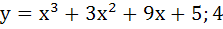 c) 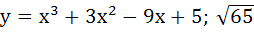 d) 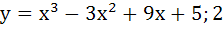
Let y = f(x) is a cubic polynomial having maximum at x = − 1 and 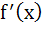 has a minimum at x = 1 and f(−1) = 10, f(1) = − 6. Find the cubic polynomial and also find the distance between the points which are maxima or minima. has a minimum at x = 1 and f(−1) = 10, f(1) = − 6. Find the cubic polynomial and also find the distance between the points which are maxima or minima. a) 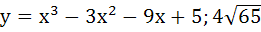 b) 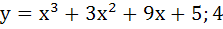 c) 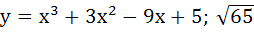 d) 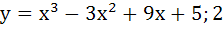
|
IIT 2005 |
|
|
1179 |
Each of the following four inequalities given below define a region in the XY–plane. One of these four regions does not have the following property: For any two points (x1, y1) and (x2, y2) in the region, point 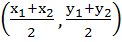 is also in the region. The inequality defining the region that does not have this property is is also in the region. The inequality defining the region that does not have this property is a) x2 + 2y2 ≤ 1 b) max (|x|, |y|) ≤ 1 c) x2 – y2 ≥ 1 d) y2 – x ≤ 0
Each of the following four inequalities given below define a region in the XY–plane. One of these four regions does not have the following property: For any two points (x1, y1) and (x2, y2) in the region, point 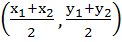 is also in the region. The inequality defining the region that does not have this property is is also in the region. The inequality defining the region that does not have this property is a) x2 + 2y2 ≤ 1 b) max (|x|, |y|) ≤ 1 c) x2 – y2 ≥ 1 d) y2 – x ≤ 0
|
IIT 1981 |
|
|
1180 |
The domain of definition of the function 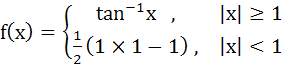 is is a) 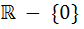 b) 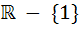 c) 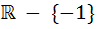 d) 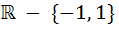
The domain of definition of the function 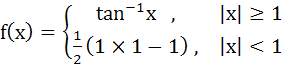 is is a) 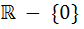 b) 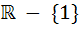 c) 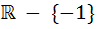 d) 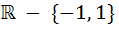
|
IIT 2002 |
|
|
1181 |
The set of values of x which ln(1 + x) ≤ x is equal to . . . . a) (−∞, −1) b) (−1, 0) c) (0, 1) d) (1, ∞)
The set of values of x which ln(1 + x) ≤ x is equal to . . . . a) (−∞, −1) b) (−1, 0) c) (0, 1) d) (1, ∞)
|
IIT 1987 |
|
|
1182 |
For any positive integers m, n (with n ≥ m), we are given that
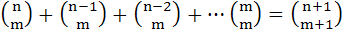
Deduce that
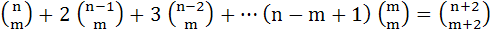
For any positive integers m, n (with n ≥ m), we are given that
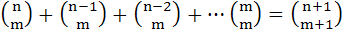
Deduce that
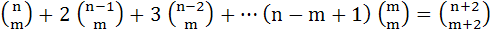
|
IIT 2000 |
|
|
1183 |
If A and B are two independent events such that P (A) > 0 and P (B) ≠ 1 then 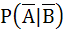 is equal to is equal to a) 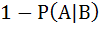 b) 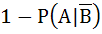 c) 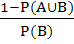 d) 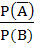
If A and B are two independent events such that P (A) > 0 and P (B) ≠ 1 then 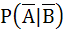 is equal to is equal to a) 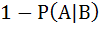 b) 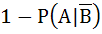 c) 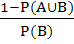 d) 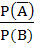
|
IIT 1980 |
|
|
1184 |
If , , 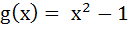 then g(f(x)) is invertible in the domain then g(f(x)) is invertible in the domain a) 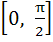 b) 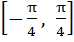 c) 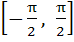 d) 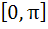
If , , 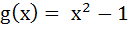 then g(f(x)) is invertible in the domain then g(f(x)) is invertible in the domain a) 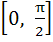 b) 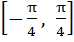 c) 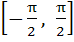 d) 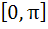
|
IIT 2004 |
|
|
1185 |
Evaluate 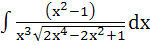 a) 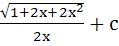 b) 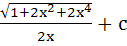 c) 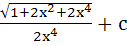 d) 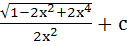
|
IIT 2006 |
|
|
1186 |
Tangents are drawn to the circle 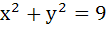 from a point on the hyperbola from a point on the hyperbola 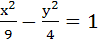 . Find the locus of the midpoint of the chord of contact. . Find the locus of the midpoint of the chord of contact.
Tangents are drawn to the circle 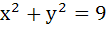 from a point on the hyperbola from a point on the hyperbola 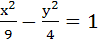 . Find the locus of the midpoint of the chord of contact. . Find the locus of the midpoint of the chord of contact.
|
IIT 2005 |
|
|
1187 |
The value of the integral is equal to a) b) c) d)
The value of the integral is equal to a) b) c) d)
|
IIT 2012 |
|
|
1188 |
Show that the integral of sinxsin2xsin3x + sec2xcos22x + sin4xcos4x is 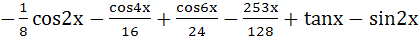
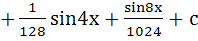
Show that the integral of sinxsin2xsin3x + sec2xcos22x + sin4xcos4x is 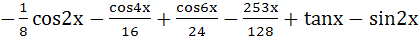
|
IIT 1979 |
|
|
1189 |
Let P (x1, y1) and Q (x2, y2), y1 < 0, y2 < 0 be the end points of the latus rectum of the ellipse x2 + 4y2 = 4. The equations of the parabolas with latus rectum PQ are a) 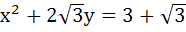 b) 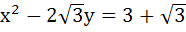 c) 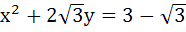 d) 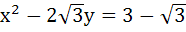
Let P (x1, y1) and Q (x2, y2), y1 < 0, y2 < 0 be the end points of the latus rectum of the ellipse x2 + 4y2 = 4. The equations of the parabolas with latus rectum PQ are a) 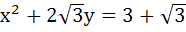 b) 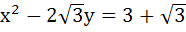 c) 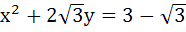 d) 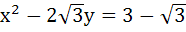
|
IIT 2008 |
|
|
1190 |
Let F : ℝ → ℝ be a thrice differentiable function. Suppose that F(1) = 0, F(3) = −4 and F′(x) < 0 for all x ε (1, 3). Let f(x) = x F(x) for all x ε ℝ.If and , then the correct expression is/are a) b) c) d)
Let F : ℝ → ℝ be a thrice differentiable function. Suppose that F(1) = 0, F(3) = −4 and F′(x) < 0 for all x ε (1, 3). Let f(x) = x F(x) for all x ε ℝ.If and , then the correct expression is/are a) b) c) d)
|
IIT 2015 |
|
|
1191 |
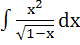 = =
a) 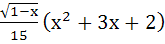 +c +c b) 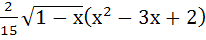 +c +c c) 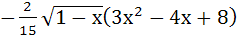 +c +c d) 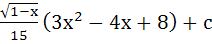
|
IIT 1980 |
|
|
1192 |
Consider the points
P: (−sin (β – α), 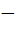 cosβ) cosβ)
Q: (cos (β – α), sinβ)
R: (−cos{(β – α) + θ}, sin (β – θ))
where 0 < α, β, θ < 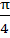 then then a) P lies on the line segment RQ b) Q lies on the line segment PR c) R lies on the line segment QP d) P, Q, R are non–collinear
Consider the points
P: (−sin (β – α), 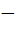 cosβ) cosβ)
Q: (cos (β – α), sinβ)
R: (−cos{(β – α) + θ}, sin (β – θ))
where 0 < α, β, θ < 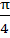 then then a) P lies on the line segment RQ b) Q lies on the line segment PR c) R lies on the line segment QP d) P, Q, R are non–collinear
|
IIT 2008 |
|
|
1193 |
One or more than one correct options The options with the values of α and L that satisfy the equation is/are a) b) c) d)
One or more than one correct options The options with the values of α and L that satisfy the equation is/are a) b) c) d)
|
IIT 2010 |
|
|
1194 |
The number of points in the interval in which attains its maximum value is a) 8 b) 2 c) 4 d) 0
The number of points in the interval in which attains its maximum value is a) 8 b) 2 c) 4 d) 0
|
IIT 2014 |
|
|
1195 |
If the integers m and n are chosen at random between 1 and 100 then the probability that a number of form 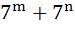 is divisible by 5, equals is divisible by 5, equals a)  b)  c)  d) 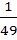
If the integers m and n are chosen at random between 1 and 100 then the probability that a number of form 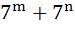 is divisible by 5, equals is divisible by 5, equals a)  b)  c)  d) 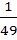
|
IIT 1999 |
|
|
1196 |
Show that the integral
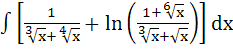 = = 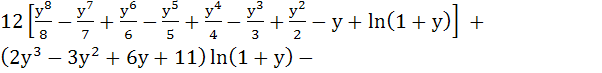
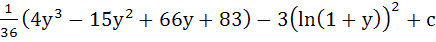
where y = x1/6
Show that the integral
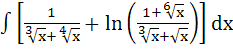 = = 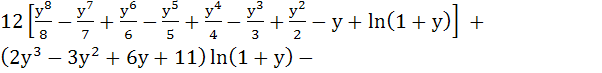
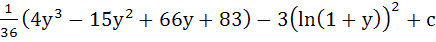
where y = x1/6
|
IIT 1992 |
|
|
1197 |
If Where takes only principal values then the value of is a) 6 b) 9 c) 8 d) 11
If Where takes only principal values then the value of is a) 6 b) 9 c) 8 d) 11
|
IIT 2015 |
|
|
1198 |
The intercept on X axis made by the tangent to the curve which is parallel to the line y = 2x are equal to a) ±1 b) ±2 c) ±3 d) ±4
The intercept on X axis made by the tangent to the curve which is parallel to the line y = 2x are equal to a) ±1 b) ±2 c) ±3 d) ±4
|
IIT 2013 |
|
|
1199 |
The common tangent to the curve x2 + y2 = 2 and the parabola y2 = 8x touch the circle at the points P, Q and the parabola at the points R, S. Then the area (in square units) of the quadrilateral PQRS is a) 3 b) 6 c) 9 d) 15
The common tangent to the curve x2 + y2 = 2 and the parabola y2 = 8x touch the circle at the points P, Q and the parabola at the points R, S. Then the area (in square units) of the quadrilateral PQRS is a) 3 b) 6 c) 9 d) 15
|
IIT 2014 |
|
|
1200 |
(One or more correct answers)
Let 0 < P (A) < 1, 0 < P (B) < 1 and P (A ∪ B) = P (A) + P (B) – P (A ∩ B) then a) P (B/A) = P (B) – P (A) b) P (Aʹ – Bʹ) = P (Aʹ) – P (Bʹ) c) P (A U B)ʹ = P (Aʹ) P (Bʹ) d) P (A/B) = P (A)
(One or more correct answers)
Let 0 < P (A) < 1, 0 < P (B) < 1 and P (A ∪ B) = P (A) + P (B) – P (A ∩ B) then a) P (B/A) = P (B) – P (A) b) P (Aʹ – Bʹ) = P (Aʹ) – P (Bʹ) c) P (A U B)ʹ = P (Aʹ) P (Bʹ) d) P (A/B) = P (A)
|
IIT 1995 |
|