|
1126 |
Let 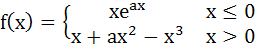
where a is a positive constant. Find the interval in which 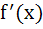 is increasing. is increasing. a) 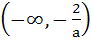 b) 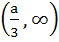 c) 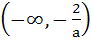 d) 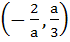
Let 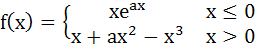
where a is a positive constant. Find the interval in which 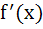 is increasing. is increasing. a) 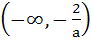 b) 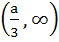 c) 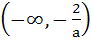 d) 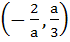
|
IIT 1996 |
|
|
1127 |
Let S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a, b, c and d denote the lengths of the sides of the quadrilateral; prove that
2 ≤ a2 + b2 + c2 + d2 ≤ 4
Let S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a, b, c and d denote the lengths of the sides of the quadrilateral; prove that
2 ≤ a2 + b2 + c2 + d2 ≤ 4
|
IIT 1997 |
|
|
1128 |
The number of ordered pairs satisfying the equations
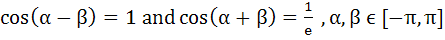 is is a) 4 b) 2 c) 0 d) 1
The number of ordered pairs satisfying the equations
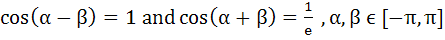 is is a) 4 b) 2 c) 0 d) 1
|
IIT 2005 |
|
|
1129 |
Let O (0, 0), A(2, 0) and 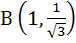 be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB which satisfies d(P, OA) ≤ d(P, OB) . d(P, AB), where d denotes the distance from the point to the corresponding line. Sketch the region R and find its area. be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB which satisfies d(P, OA) ≤ d(P, OB) . d(P, AB), where d denotes the distance from the point to the corresponding line. Sketch the region R and find its area. a) 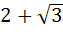 b) 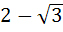 c) 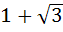 d) 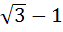
Let O (0, 0), A(2, 0) and 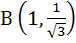 be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB which satisfies d(P, OA) ≤ d(P, OB) . d(P, AB), where d denotes the distance from the point to the corresponding line. Sketch the region R and find its area. be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB which satisfies d(P, OA) ≤ d(P, OB) . d(P, AB), where d denotes the distance from the point to the corresponding line. Sketch the region R and find its area. a) 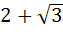 b) 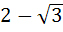 c) 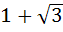 d) 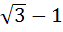
|
IIT 1997 |
|
|
1130 |
Let f(x) be a continuous function given by
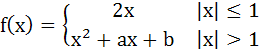 Find the area of the region in the third quadrant bounded by the curve x = − 2y2 and y = f(x) lying on the left of the line 8x + 1 = 0. a) 192 b) 320 c) 761/192 d) 320/761
Let f(x) be a continuous function given by
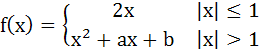 Find the area of the region in the third quadrant bounded by the curve x = − 2y2 and y = f(x) lying on the left of the line 8x + 1 = 0. a) 192 b) 320 c) 761/192 d) 320/761
|
IIT 1999 |
|
|
1131 |
Let d be the perpendicular distance from the centre of the ellipse 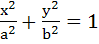 to the tangent at a point P on the ellipse. Let F1 and F2 be the two focii of the ellipse, then show that to the tangent at a point P on the ellipse. Let F1 and F2 be the two focii of the ellipse, then show that 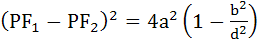
Let d be the perpendicular distance from the centre of the ellipse 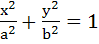 to the tangent at a point P on the ellipse. Let F1 and F2 be the two focii of the ellipse, then show that to the tangent at a point P on the ellipse. Let F1 and F2 be the two focii of the ellipse, then show that 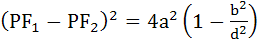
|
IIT 1995 |
|
|
1132 |
Find the area of the region bounded by the curves y = x2, y = |2 – x2| and y = 2 which lies to the right of the line x = 1. a) 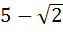 b)  c) 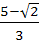 d) 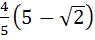
Find the area of the region bounded by the curves y = x2, y = |2 – x2| and y = 2 which lies to the right of the line x = 1. a) 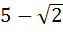 b)  c) 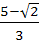 d) 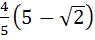
|
IIT 2002 |
|
|
1133 |
Prove that in an ellipse the perpendicular from a focus upon a tangent and the line joining the centre of the ellipse to the point of contact meet on the corresponding directrix.
Prove that in an ellipse the perpendicular from a focus upon a tangent and the line joining the centre of the ellipse to the point of contact meet on the corresponding directrix.
|
IIT 2002 |
|
|
1134 |
A curve passing through the point 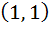 has the property that the perpendicular distance of the origin from the normal at any point P of the curve is equal to the distance of P from the X-axis. Determine the equation of the curve. has the property that the perpendicular distance of the origin from the normal at any point P of the curve is equal to the distance of P from the X-axis. Determine the equation of the curve.
A curve passing through the point 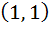 has the property that the perpendicular distance of the origin from the normal at any point P of the curve is equal to the distance of P from the X-axis. Determine the equation of the curve. has the property that the perpendicular distance of the origin from the normal at any point P of the curve is equal to the distance of P from the X-axis. Determine the equation of the curve.
|
IIT 1999 |
|
|
1135 |
Let f : ℝ → ℝ be any function. Define g : ℝ → ℝ by g(x) = |f(x)| for all x. Then g is a) Onto if f is onto b) One–one if f is one–one c) Continuous if f is continuous d) Differentiable if f is differentiable
Let f : ℝ → ℝ be any function. Define g : ℝ → ℝ by g(x) = |f(x)| for all x. Then g is a) Onto if f is onto b) One–one if f is one–one c) Continuous if f is continuous d) Differentiable if f is differentiable
|
IIT 2000 |
|
|
1136 |
f(x) is a differentiable function and g(x) is a double differentiable function such that 
If 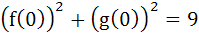 prove that there exists some c ε (−3, 3) such that prove that there exists some c ε (−3, 3) such that 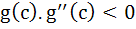 . .
|
IIT 2005 |
|
|
1137 |
If (x – r) is a factor of the polynomial f(x) = anxn + . . . + a0, repeated m times (1 < m ≤ n) then r is a root of 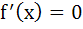 repeated m times. repeated m times. a) True b) False
If (x – r) is a factor of the polynomial f(x) = anxn + . . . + a0, repeated m times (1 < m ≤ n) then r is a root of 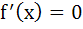 repeated m times. repeated m times. a) True b) False
|
IIT 1983 |
|
|
1138 |
Let a solution y = y (x) of the differential equation 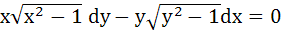 satisfies satisfies 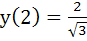 Statement 1 : 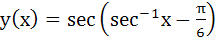 Statement 2 : 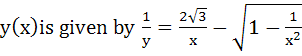 a) Statement 1 is true. Statement 2 is true. Statement 2 is a correct explanation of statement 1. b) Statement 1 is true. Statement 2 is true. Statement 2 is not a correct explanation of statement 1 c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
Let a solution y = y (x) of the differential equation 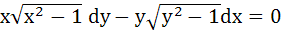 satisfies satisfies 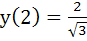 Statement 1 : 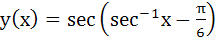 Statement 2 : 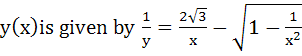 a) Statement 1 is true. Statement 2 is true. Statement 2 is a correct explanation of statement 1. b) Statement 1 is true. Statement 2 is true. Statement 2 is not a correct explanation of statement 1 c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
|
IIT 2008 |
|
|
1139 |
A hyperbola having the transverse axis of length 2sinθ is confocal with the ellipse 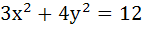 . Then its equation is . Then its equation is a) 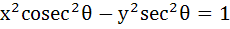 b) 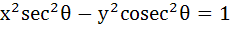 c) 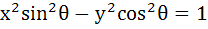 d) 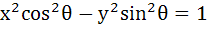
A hyperbola having the transverse axis of length 2sinθ is confocal with the ellipse 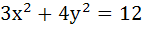 . Then its equation is . Then its equation is a) 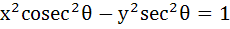 b) 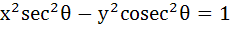 c) 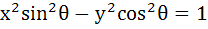 d) 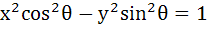
|
IIT 2007 |
|
|
1140 |
The angle between the pair of tangents from a point P to the parabola y2 = 4ax is 45°. Show that the locus of the point P is a hyperbola.
The angle between the pair of tangents from a point P to the parabola y2 = 4ax is 45°. Show that the locus of the point P is a hyperbola.
|
IIT 1998 |
|
|
1141 |
The integral is equal to a) b) c) d)
The integral is equal to a) b) c) d)
|
IIT 2014 |
|
|
1142 |
A box contains 24 identical balls of which 12 are white and 12 are black. The balls are drawn at random from the box one at a time with replacement. The probability that a white ball is drawn for the fourth time on the seventh draw is a) 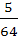 b) 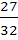 c) 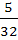 d) 
A box contains 24 identical balls of which 12 are white and 12 are black. The balls are drawn at random from the box one at a time with replacement. The probability that a white ball is drawn for the fourth time on the seventh draw is a) 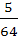 b) 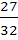 c) 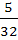 d) 
|
IIT 1984 |
|
|
1143 |
Let F : ℝ → ℝ be a thrice differentiable function. Suppose that F(1) = 0, F(3) = −4 and F′(x) < 0 for all x ε (1, 3). Let f(x) = x F(x) for all x ε ℝ.The correct statement(s) is/are a) f′(1) < 0 b) f(2) < 0 c) f′(x) ≠ 0 for every x ε (1, 3) d) f′(x) = 0 for some x ε (1, 3)
Let F : ℝ → ℝ be a thrice differentiable function. Suppose that F(1) = 0, F(3) = −4 and F′(x) < 0 for all x ε (1, 3). Let f(x) = x F(x) for all x ε ℝ.The correct statement(s) is/are a) f′(1) < 0 b) f(2) < 0 c) f′(x) ≠ 0 for every x ε (1, 3) d) f′(x) = 0 for some x ε (1, 3)
|
IIT 2015 |
|
|
1144 |
Let A, B , C be three mutually independent events. Consider the two statements S1 and S2 S1 : A and B ∪ C are independent are independent S2 : A and B ∩ C are independent. Then a) Both S1 and S2 are true b) Only S1 is true c) Only S2 is true d) Neither S1 nor S2 is true
Let A, B , C be three mutually independent events. Consider the two statements S1 and S2 S1 : A and B ∪ C are independent are independent S2 : A and B ∩ C are independent. Then a) Both S1 and S2 are true b) Only S1 is true c) Only S2 is true d) Neither S1 nor S2 is true
|
IIT 1994 |
|
|
1145 |
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The point of contacts of C with its sides PQ, QR and RP are D, E, F respectively. The line PQ is given by 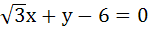 and the point D is and the point D is 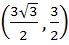 . Further, it is given that the origin and the centre of C are on the same side of the line PQ. Equations of lines QR and RP are . Further, it is given that the origin and the centre of C are on the same side of the line PQ. Equations of lines QR and RP are a) 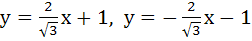 b) 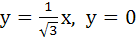 c) 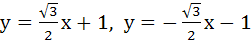 d) 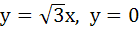
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The point of contacts of C with its sides PQ, QR and RP are D, E, F respectively. The line PQ is given by 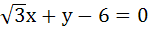 and the point D is and the point D is 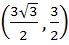 . Further, it is given that the origin and the centre of C are on the same side of the line PQ. Equations of lines QR and RP are . Further, it is given that the origin and the centre of C are on the same side of the line PQ. Equations of lines QR and RP are a) 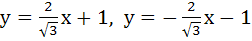 b) 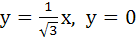 c) 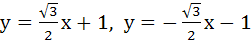 d) 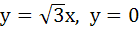
|
IIT 2008 |
|
|
1146 |
Let f(x) = 7tan8x + 7tan6x – 3tan4x – 3tan2x for all Then the correct expression(s) is (are) a) b) c) d)
Let f(x) = 7tan8x + 7tan6x – 3tan4x – 3tan2x for all Then the correct expression(s) is (are) a) b) c) d)
|
IIT 2015 |
|
|
1147 |
Consider the lines
L1: x + 3y – 5 = 0, L2: 3x – ky – 1 = 0, L3: 5x + 2y – 12 = 0.
Match the statement/expressions in column 1 with the statement/expression in column 2. | Column 1 | Column 2 | | A) L1, L2, L3 are concurrent if | p) k = − 9 | | B) One of L1, L2, L3 is parallel to at least one of the other two | q) 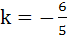 | | C) L1, L2, L3 form a triangle if | r) 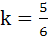 | | D) L1, L2, L3 do not form a triangle if | s) k = 5 |
Consider the lines
L1: x + 3y – 5 = 0, L2: 3x – ky – 1 = 0, L3: 5x + 2y – 12 = 0.
Match the statement/expressions in column 1 with the statement/expression in column 2. | Column 1 | Column 2 | | A) L1, L2, L3 are concurrent if | p) k = − 9 | | B) One of L1, L2, L3 is parallel to at least one of the other two | q) 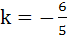 | | C) L1, L2, L3 form a triangle if | r) 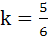 | | D) L1, L2, L3 do not form a triangle if | s) k = 5 |
|
IIT 2008 |
|
|
1148 |
The number of quadratic polynomials f(x) with non-negative integer coefficients ≤ 3 satisfying f(0) = 0 and is a) 8 b) 2 c) 4 d) 0
The number of quadratic polynomials f(x) with non-negative integer coefficients ≤ 3 satisfying f(0) = 0 and is a) 8 b) 2 c) 4 d) 0
|
IIT 2014 |
|
|
1149 |
A function f : ℝ → ℝ, where ℝ is the set of real numbers, is defined by 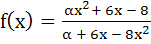 . Find the interval of values of α for which f is onto. Is the function one to one for α= 3? Justify your answer. . Find the interval of values of α for which f is onto. Is the function one to one for α= 3? Justify your answer.
A function f : ℝ → ℝ, where ℝ is the set of real numbers, is defined by 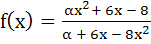 . Find the interval of values of α for which f is onto. Is the function one to one for α= 3? Justify your answer. . Find the interval of values of α for which f is onto. Is the function one to one for α= 3? Justify your answer.
|
IIT 1996 |
|
|
1150 |
Let f : ℝ → ℝ be a function defined by where [x] denotes the greatest integer less than or equal to x. If then the value of (4I – 1) is a) 1 b) 3 c) 2 d) 0
Let f : ℝ → ℝ be a function defined by where [x] denotes the greatest integer less than or equal to x. If then the value of (4I – 1) is a) 1 b) 3 c) 2 d) 0
|
IIT 2015 |
|