|
1051 |
Let U1 = 1, U2 = 1, Un + 2 = Un + 1 + Un, n > 1. Use mathematical induction to show that
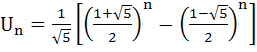
for all integers n > 1
Let U1 = 1, U2 = 1, Un + 2 = Un + 1 + Un, n > 1. Use mathematical induction to show that
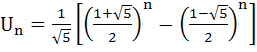
for all integers n > 1
|
IIT 1981 |
|
|
1052 |
Let f(x) = (1 – x)2 sin2x + x2Consider the statementsStatement 1: There exists some x ∈ ℝ such that f(x) + 2x = 2(1 + x2)Statement 2: There exists some x ∈ ℝ such that 2f(x) + 1 = 2x(x + 1) a) Both 1 and 2 are true b) 1 is true and 2 is false c) 1 is false and 2 is true d) Both 1 and 2 are false
Let f(x) = (1 – x)2 sin2x + x2Consider the statementsStatement 1: There exists some x ∈ ℝ such that f(x) + 2x = 2(1 + x2)Statement 2: There exists some x ∈ ℝ such that 2f(x) + 1 = 2x(x + 1) a) Both 1 and 2 are true b) 1 is true and 2 is false c) 1 is false and 2 is true d) Both 1 and 2 are false
|
IIT 2013 |
|
|
1053 |
Let z and ω be two complex numbers such that |z| ≤ 1, |ω| ≤ 1 and 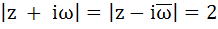 then z equals then z equals a) 1 or i b) i or –i c) 1 or –1 d) i or –1
Let z and ω be two complex numbers such that |z| ≤ 1, |ω| ≤ 1 and 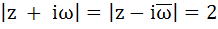 then z equals then z equals a) 1 or i b) i or –i c) 1 or –1 d) i or –1
|
IIT 1995 |
|
|
1054 |
Given
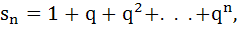 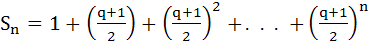
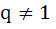
Prove that
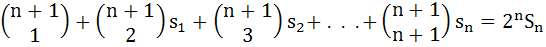
|
IIT 1984 |
|
|
1055 |
The coordinates of the in centre of the triangle that has the co ordinates of the mid points of its sides as (0, 1), (1, 1) and (1, 0) is a) b) c) d)
The coordinates of the in centre of the triangle that has the co ordinates of the mid points of its sides as (0, 1), (1, 1) and (1, 0) is a) b) c) d)
|
IIT 2013 |
|
|
1056 |
Using mathematical induction, prove that 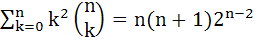 for n > 1 for n > 1
Using mathematical induction, prove that 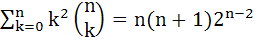 for n > 1 for n > 1
|
IIT 1986 |
|
|
1057 |
If f(x) = 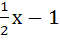 then on the interval [0, π] then on the interval [0, π] a) tan 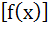 and and 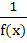 are both continuous are both continuous b) tan 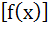 and and 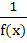 are both discontinuous are both discontinuous c) tan 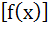 and and 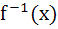 are both continuous are both continuous d) tan 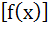 is continuous but is continuous but 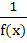 is not is not
|
IIT 1989 |
|
|
1058 |
One or more than one correct option A ray of light along gets reflected upon reaching X- axis, the equation of the reflected ray is a) b) c) d)
One or more than one correct option A ray of light along gets reflected upon reaching X- axis, the equation of the reflected ray is a) b) c) d)
|
IIT 2013 |
|
|
1059 |
If 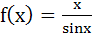 and and 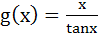 where 0 < x ≤1, then in this interval where 0 < x ≤1, then in this interval a) Both f (x) and g (x) are increasing functions b) Both f (x) and g (x) are decreasing functions c) f (x) is an increasing function d) g (x) is an increasing function
If 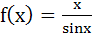 and and 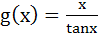 where 0 < x ≤1, then in this interval where 0 < x ≤1, then in this interval a) Both f (x) and g (x) are increasing functions b) Both f (x) and g (x) are decreasing functions c) f (x) is an increasing function d) g (x) is an increasing function
|
IIT 1997 |
|
|
1060 |
The number of common tangents to the circles x2 + y2 – 4x − 6y – 12 = 0 and x2 + y2 + 6x + 18y + 26 = 0 is a) 1 b) 2 c) 3 d) 4
The number of common tangents to the circles x2 + y2 – 4x − 6y – 12 = 0 and x2 + y2 + 6x + 18y + 26 = 0 is a) 1 b) 2 c) 3 d) 4
|
IIT 2015 |
|
|
1061 |
Let p ≥ 3 be an integer and α, β be the roots of x2 – (p + 1) x + 1 = 0. Using mathematical induction show that αn + βn
i) is an integer
ii) and is not divisible by p.
Let p ≥ 3 be an integer and α, β be the roots of x2 – (p + 1) x + 1 = 0. Using mathematical induction show that αn + βn
i) is an integer
ii) and is not divisible by p.
|
IIT 1992 |
|
|
1062 |
The function 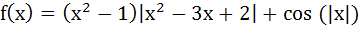 is not differentiable at is not differentiable at a) – 1 b) 0 c) 1 d) 2
The function 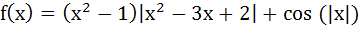 is not differentiable at is not differentiable at a) – 1 b) 0 c) 1 d) 2
|
IIT 1999 |
|
|
1063 |
One or more than one correct option Let RS be a diameter of the circle x2 + y2 = 1 where S is the point (1, 0). Let P be a variable point (other than R and S) on the circle and the tangents to the circle at S and P meet at the point Q. The normal to the circle at P intersect a line drawn through Q parallel to RS at a point E. Then the locus of E passes through the point(s) a) b) c) d)
One or more than one correct option Let RS be a diameter of the circle x2 + y2 = 1 where S is the point (1, 0). Let P be a variable point (other than R and S) on the circle and the tangents to the circle at S and P meet at the point Q. The normal to the circle at P intersect a line drawn through Q parallel to RS at a point E. Then the locus of E passes through the point(s) a) b) c) d)
|
IIT 2016 |
|
|
1064 |
If x is not an integral multiple of 2π use mathematical induction to prove that
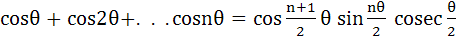
If x is not an integral multiple of 2π use mathematical induction to prove that
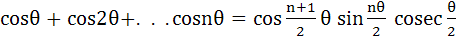
|
IIT 1994 |
|
|
1065 |
A circle passing through (1, −2) and touching the axis of X at (3, 0) also passes through the point a) (−5, 2) b) (2, −5) c) (5, −2) d) (−2, 5)
A circle passing through (1, −2) and touching the axis of X at (3, 0) also passes through the point a) (−5, 2) b) (2, −5) c) (5, −2) d) (−2, 5)
|
IIT 2013 |
|
|
1066 |
The circles 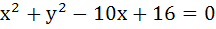 and and 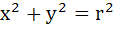 intersect each other in distinct points if intersect each other in distinct points if a) r < 2 b) r > 8 c) 2 < r < 8 d) 2 ≤ r ≤ 8
The circles 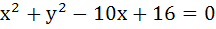 and and 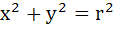 intersect each other in distinct points if intersect each other in distinct points if a) r < 2 b) r > 8 c) 2 < r < 8 d) 2 ≤ r ≤ 8
|
IIT 1994 |
|
|
1067 |
Prove by induction that
Pn = Aαn + Bβn for all n ≥ 1
Where α and β are roots of the quadratic equation
x2 – (1 – P) x – P (1 – P) = 0,
P1 = 1, P2 = 1 – P2, . . .,
Pn = (1 – P) Pn – 1 + P (1 – P) Pn – 2  n ≥ 3, n ≥ 3,
and 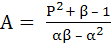 , , 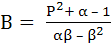
|
IIT 2000 |
|
|
1068 |
Let P be a point on the parabola y2 = 8x which is at a minimum distance from the centre C of the circle x2 + (y + 6)2 = 1. Then the equation of the circle passing through C and having its centre at P is a) x2 + y2 – 4x + 8y + 12 = 0 b) x2 + y2 –x + 4y − 12 = 0 c) x2 + y2 –x + 2y − 24 = 0 d) x2 + y2 – 4x + 9y + 18 = 0
Let P be a point on the parabola y2 = 8x which is at a minimum distance from the centre C of the circle x2 + (y + 6)2 = 1. Then the equation of the circle passing through C and having its centre at P is a) x2 + y2 – 4x + 8y + 12 = 0 b) x2 + y2 –x + 4y − 12 = 0 c) x2 + y2 –x + 2y − 24 = 0 d) x2 + y2 – 4x + 9y + 18 = 0
|
IIT 2016 |
|
|
1069 |
Let 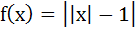 then points where f (x) is not differentiable is (are) then points where f (x) is not differentiable is (are) a) 0 b) 1 c) ± 1 d) 0, ± 1
Let 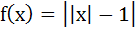 then points where f (x) is not differentiable is (are) then points where f (x) is not differentiable is (are) a) 0 b) 1 c) ± 1 d) 0, ± 1
|
IIT 2005 |
|
|
1070 |
The slope of the line touching both parabolas y2 = 4x and x2 = −32y is a) b) c) d)
The slope of the line touching both parabolas y2 = 4x and x2 = −32y is a) b) c) d)
|
IIT 2014 |
|
|
1071 |
Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and QR intersect at a point x on the circumference of the circle, then 2r equals a) 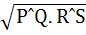 b) 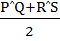 c) 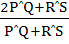 d) 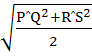
Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and QR intersect at a point x on the circumference of the circle, then 2r equals a) 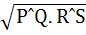 b) 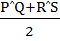 c) 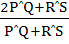 d) 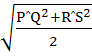
|
IIT 2001 |
|
|
1072 |
Multiple choices Let [x] denote the greatest integer less than or equal to x. If f (x) = [xsinπx] then f(x) is a) Continuous at x = 0 b) Continuous in 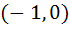 c) f (x) is differentiable at x = 1 d) differentiable in 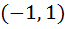 e) None of these
Multiple choices Let [x] denote the greatest integer less than or equal to x. If f (x) = [xsinπx] then f(x) is a) Continuous at x = 0 b) Continuous in 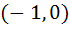 c) f (x) is differentiable at x = 1 d) differentiable in 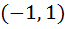 e) None of these
|
IIT 1986 |
|
|
1073 |
Let 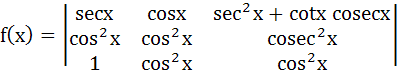 then then 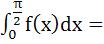 a) 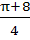 b) 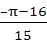 c) 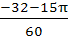 d) 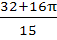
|
IIT 1987 |
|
|
1074 |
Let a, r, s, t be non-zero real numbers. Let P(at2, 2at), Q, R(ar2, 2ar and S(as2, 2as) be distinct points on the parabola y2 = 4ax. Suppose PQ is the focal chord and QR and PK are parallel, where K is point (2a, 0) The value of r is a) b) c) d)
Let a, r, s, t be non-zero real numbers. Let P(at2, 2at), Q, R(ar2, 2ar and S(as2, 2as) be distinct points on the parabola y2 = 4ax. Suppose PQ is the focal chord and QR and PK are parallel, where K is point (2a, 0) The value of r is a) b) c) d)
|
IIT 2014 |
|
|
1075 |
Find all solutions of 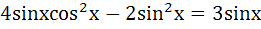 a) 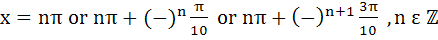 b) 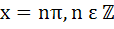 c) 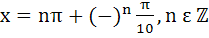 d) 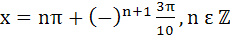
Find all solutions of 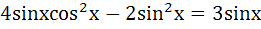 a) 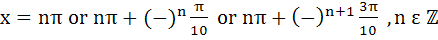 b) 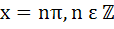 c) 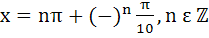 d) 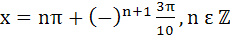
|
IIT 1983 |
|