|
76 |
The number of points of intersection of the two curves y = 2sinx and y = 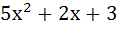 is is a) 0 b) 1 c) 2 d) 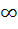
The number of points of intersection of the two curves y = 2sinx and y = 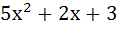 is is a) 0 b) 1 c) 2 d) 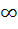
|
IIT 1994 |
01:51 min
|
|
77 |
If the system of equations x – ky – z = 0 kx – y –z = 0 x + y –z = 0 has a non zero solution then possible values of k are a) −1, 2 b) 1, 2 c) 0, 1 d) −1, 1
If the system of equations x – ky – z = 0 kx – y –z = 0 x + y –z = 0 has a non zero solution then possible values of k are a) −1, 2 b) 1, 2 c) 0, 1 d) −1, 1
|
IIT 2000 |
02:26 min
|
|
78 |
The axis of the parabola is along the line 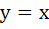 and the distance of the vertex and focus from origin are and the distance of the vertex and focus from origin are 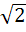 and and 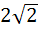 respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is a) 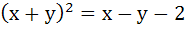 b) 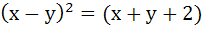 c) 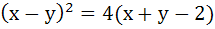 d) 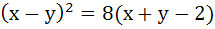
The axis of the parabola is along the line 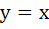 and the distance of the vertex and focus from origin are and the distance of the vertex and focus from origin are 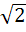 and and 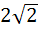 respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is a) 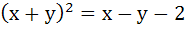 b) 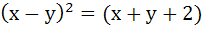 c) 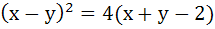 d) 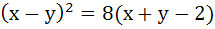
|
IIT 2006 |
05:21 min
|
|
79 |
The roots of the equation 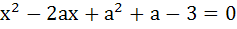 are real and less than 3, then are real and less than 3, then a) a < 2 b) 2 < a < 3 c) 3 ≤ a ≤ 4 d) a > 4
The roots of the equation 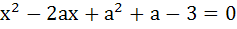 are real and less than 3, then are real and less than 3, then a) a < 2 b) 2 < a < 3 c) 3 ≤ a ≤ 4 d) a > 4
|
IIT 1999 |
02:39 min
|
|
80 |
Given 2x – y – z = 2, x – 2y + z = − 4, x + y + λz = 4 then the value of λ such that the given system of equations has no solution is a) 3 b) −2 c) 0 d) −3
Given 2x – y – z = 2, x – 2y + z = − 4, x + y + λz = 4 then the value of λ such that the given system of equations has no solution is a) 3 b) −2 c) 0 d) −3
|
IIT 2004 |
03:35 min
|
|
81 |
Find all non zero complex numbers satisfying  . .
Find all non zero complex numbers satisfying  . .
|
IIT 1996 |
04:39 min
|
|
82 |
Sketch the region bounded by the curves y = x2 and 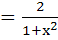 . Find the area. . Find the area. a)  b)  c) 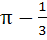 d) 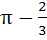
Sketch the region bounded by the curves y = x2 and 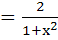 . Find the area. . Find the area. a)  b)  c) 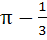 d) 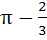
|
IIT 1992 |
06:17 min
|
|
83 |
Find the equation of the normal to the curve 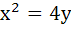 which passes through the point (1, 2). which passes through the point (1, 2).
Find the equation of the normal to the curve 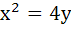 which passes through the point (1, 2). which passes through the point (1, 2).
|
IIT 1984 |
03:23 min
|
|
84 |
(Multiple choices)
The determinant
 is equal to zero if is equal to zero if a) a, b, c are in arithmetic progression b) a, b, c are in geometric progression c) a, b, c are in harmonic progression d) α is a root of the equation ax2 + bx + c = 0 e) x – α is a factor of ax2 + 2bx + c
(Multiple choices)
The determinant
 is equal to zero if is equal to zero if a) a, b, c are in arithmetic progression b) a, b, c are in geometric progression c) a, b, c are in harmonic progression d) α is a root of the equation ax2 + bx + c = 0 e) x – α is a factor of ax2 + 2bx + c
|
IIT 1986 |
03:09 min
|
|
85 |
Let f(x) = 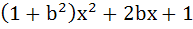 and m(b) be the minimum value of f(x). As b varies, range of m(b) is and m(b) be the minimum value of f(x). As b varies, range of m(b) is a) 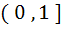 b) [ 0, 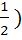 c) [ 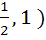 d) 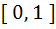
Let f(x) = 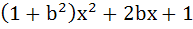 and m(b) be the minimum value of f(x). As b varies, range of m(b) is and m(b) be the minimum value of f(x). As b varies, range of m(b) is a) 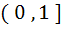 b) [ 0, 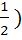 c) [ 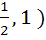 d) 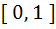
|
IIT 2001 |
03:22 min
|
|
86 |
At any point P on the parabola 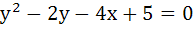 , a tangent is drawn which meets the directrix at Q. Find the locus of the point R which divides QP externally in the ratio , a tangent is drawn which meets the directrix at Q. Find the locus of the point R which divides QP externally in the ratio 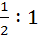 . .
At any point P on the parabola 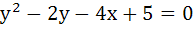 , a tangent is drawn which meets the directrix at Q. Find the locus of the point R which divides QP externally in the ratio , a tangent is drawn which meets the directrix at Q. Find the locus of the point R which divides QP externally in the ratio 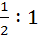 . .
|
IIT 2004 |
06:48 min
|
|
87 |
The set of all real numbers x for which 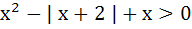 is is a) 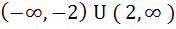 b) 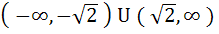 c) 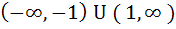 d) 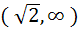
The set of all real numbers x for which 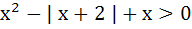 is is a) 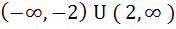 b) 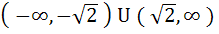 c) 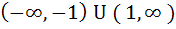 d) 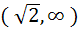
|
IIT 2002 |
03:01 min
|
|
88 |
The cube roots of unity when represented on argand diagram form the vertices of an equilateral triangle. a) True b) False
The cube roots of unity when represented on argand diagram form the vertices of an equilateral triangle. a) True b) False
|
IIT 1988 |
03:08 min
|
|
89 |
If 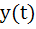 is a solution of is a solution of 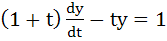 and and 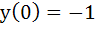 then then 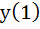 is equal to is equal to a) 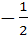 b)  c) 1 d) 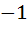
If 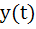 is a solution of is a solution of 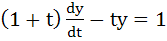 and and 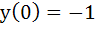 then then 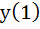 is equal to is equal to a) 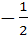 b)  c) 1 d) 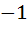
|
IIT 2000 |
03:33 min
|
|
90 |
If one root is square of the other root of the equation 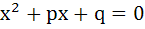 then the relation between p and q is then the relation between p and q is a) 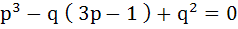 b) 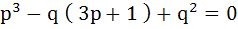 c) 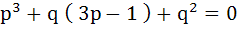 d) 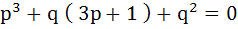
If one root is square of the other root of the equation 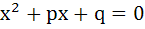 then the relation between p and q is then the relation between p and q is a) 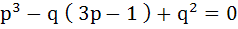 b) 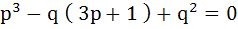 c) 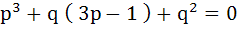 d) 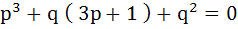
|
IIT 2004 |
03:14 min
|
|
91 |
If a ≠ p, b ≠ q, c ≠ r and
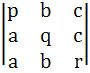 = 0 = 0 Then find the value of
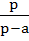 + + 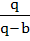 + + 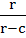 a) 0 b) 1 c) 2 d) 3
If a ≠ p, b ≠ q, c ≠ r and
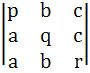 = 0 = 0 Then find the value of
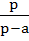 + + 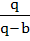 + + 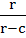 a) 0 b) 1 c) 2 d) 3
|
IIT 1991 |
03:41 min
|
|
92 |
The radius of the circle passing through the focii of the ellipse 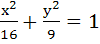 and having centre at (0, 3) is and having centre at (0, 3) is a) 4 b) 3 c) 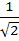 d) 
The radius of the circle passing through the focii of the ellipse 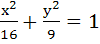 and having centre at (0, 3) is and having centre at (0, 3) is a) 4 b) 3 c) 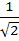 d) 
|
IIT 1995 |
01:53 min
|
|
93 |
The number of solutions of the pair of equations
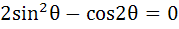 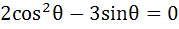
in the interval [ 0, 2π ] is
a) 0 b) 1 c) 2 d) 4
The number of solutions of the pair of equations
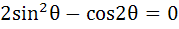 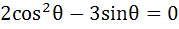
in the interval [ 0, 2π ] is
a) 0 b) 1 c) 2 d) 4
|
IIT 2007 |
07:12 min
|
|
94 |
Multiple choice question On the ellipse 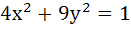 the points at which the tangents are parallel to the line the points at which the tangents are parallel to the line 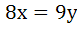 are are a) 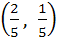 b) 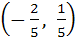 c) 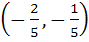 d) 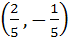
Multiple choice question On the ellipse 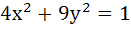 the points at which the tangents are parallel to the line the points at which the tangents are parallel to the line 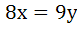 are are a) 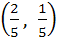 b) 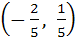 c) 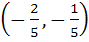 d) 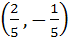
|
IIT 1999 |
03:37 min
|
|
95 |
The equation 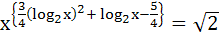 has has a) At least one real solution b) Exactly three real solutions c) Has exactly one irrational solution d) Complex roots
The equation 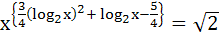 has has a) At least one real solution b) Exactly three real solutions c) Has exactly one irrational solution d) Complex roots
|
IIT 1989 |
03:53 min
|
|
96 |
Show that for for any triangle with sides a, b, c
3 (ab + bc + ac) ≤ (a + b + c)2 < 4 (ab + bc + ca)
Show that for for any triangle with sides a, b, c
3 (ab + bc + ac) ≤ (a + b + c)2 < 4 (ab + bc + ca)
|
IIT 1979 |
03:38 min
|
|
97 |
The solution set of equation 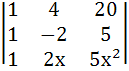 = 0 is ………. = 0 is ………. a) {0} b) {1, 2} c) {−1, 2} d) {−1, −2}
The solution set of equation 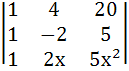 = 0 is ………. = 0 is ………. a) {0} b) {1, 2} c) {−1, 2} d) {−1, −2}
|
IIT 1981 |
02:12 min
|
|
98 |
An ellipse has eccentricity  and one of the focus at the point and one of the focus at the point 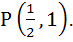 It’s one directrix is the common tangent near to the point P to the circle It’s one directrix is the common tangent near to the point P to the circle 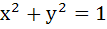 and the hyperbola and the hyperbola 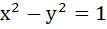 . Then the equation of the ellipse in the statement form is . . . . . . Then the equation of the ellipse in the statement form is . . . . .
|
IIT 1996 |
07:07 min
|
|
99 |
The equation 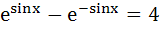 has has a) no real solutions b) one real solution c) two real solutions d) infinite real solutions
The equation 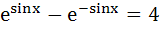 has has a) no real solutions b) one real solution c) two real solutions d) infinite real solutions
|
IIT 1982 |
03:09 min
|
|
100 |
For positive numbers x, y and z the numerical value of the determinant
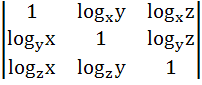 is ……….. is ……….. a) 1 b) –1 c) ±1 d) 0
For positive numbers x, y and z the numerical value of the determinant
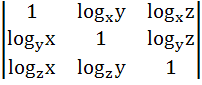 is ……….. is ……….. a) 1 b) –1 c) ±1 d) 0
|
IIT 1993 |
02:04 min
|