|
951 |
If arg(z) < 0 then arg(−z) – arg(z) is equal to a) π b) –π c) – π/2 d) π/2
If arg(z) < 0 then arg(−z) – arg(z) is equal to a) π b) –π c) – π/2 d) π/2
|
IIT 2000 |
|
|
952 |
Multiple choice f(x) is a cubic polynomial with f(2) = 18 and f(1) = − 1. Also f(x) has a local maxima at x = − 1 and 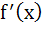 has a local minima at x = 0 then has a local minima at x = 0 then a) The distance between (− 1, 2) and (a, f(a)), where x = a is the point of local minimum, is 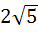 b) f(x) is increasing for 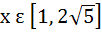 c) f(x) has a local minima at x = 1 d) The value of f(0) = 15
Multiple choice f(x) is a cubic polynomial with f(2) = 18 and f(1) = − 1. Also f(x) has a local maxima at x = − 1 and 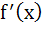 has a local minima at x = 0 then has a local minima at x = 0 then a) The distance between (− 1, 2) and (a, f(a)), where x = a is the point of local minimum, is 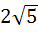 b) f(x) is increasing for 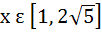 c) f(x) has a local minima at x = 1 d) The value of f(0) = 15
|
IIT 2006 |
|
|
953 |
From the point A (0, 3) on the circle 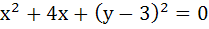 , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . . , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . .
From the point A (0, 3) on the circle 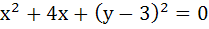 , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . . , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . .
|
IIT 1986 |
|
|
954 |
In Δ ABC the median to the side BC is of length 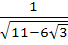 and divides ∠A into 30° and 45°. Then find the length of side BC. and divides ∠A into 30° and 45°. Then find the length of side BC. a) 1 b) 2 c) 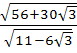 d) 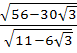
In Δ ABC the median to the side BC is of length 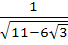 and divides ∠A into 30° and 45°. Then find the length of side BC. and divides ∠A into 30° and 45°. Then find the length of side BC. a) 1 b) 2 c) 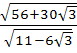 d) 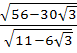
|
IIT 1985 |
|
|
955 |
If f is an even function defined on (−5, 5) then the real values of x satisfying the equation f (x) = 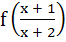 are …………… are …………… a) 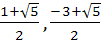 b) 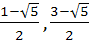 c) 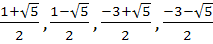 d) 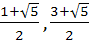
If f is an even function defined on (−5, 5) then the real values of x satisfying the equation f (x) = 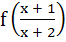 are …………… are …………… a) 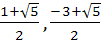 b) 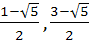 c) 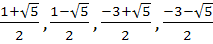 d) 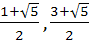
|
IIT 1996 |
|
|
956 |
If ω(≠1) be a cube root of unity and 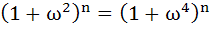 then the least positive value of n is then the least positive value of n is a) 2 b) 3 c) 5 d) 6
If ω(≠1) be a cube root of unity and 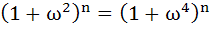 then the least positive value of n is then the least positive value of n is a) 2 b) 3 c) 5 d) 6
|
IIT 2004 |
|
|
957 |
A circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in the circle is . . . . .
A circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in the circle is . . . . .
|
IIT 1994 |
|
|
958 |
The number of all possible triplets 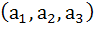 such that such that
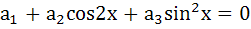 for all x is for all x is a) Zero b) One c) Three d) Infinite e) None
The number of all possible triplets 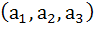 such that such that
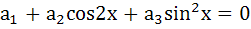 for all x is for all x is a) Zero b) One c) Three d) Infinite e) None
|
IIT 1987 |
|
|
959 |
A swimmer S is in the sea at a distance d km. from the closest point A on a straight shore. The house of the swimmer is on the shore at a distance L km. from A. He can swim at a speed of
u km/hour and walk at a speed of v km/hr (v > u). At what point on the shore should he land so that he reaches his house in the shortest possible time. a) 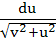 b) 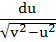 c) 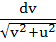 d) 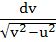
A swimmer S is in the sea at a distance d km. from the closest point A on a straight shore. The house of the swimmer is on the shore at a distance L km. from A. He can swim at a speed of
u km/hour and walk at a speed of v km/hr (v > u). At what point on the shore should he land so that he reaches his house in the shortest possible time. a) 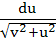 b) 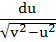 c) 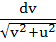 d) 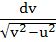
|
IIT 1983 |
|
|
960 |
Sketch the region bounded by the curves
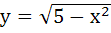 and y = |x – 1| and y = |x – 1|
and find its area. a) 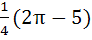 b) 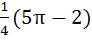 c) 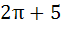 d) 5π + 2
Sketch the region bounded by the curves
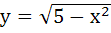 and y = |x – 1| and y = |x – 1|
and find its area. a) 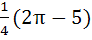 b) 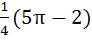 c) 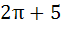 d) 5π + 2
|
IIT 1985 |
|
|
961 |
Tangents are drawn from the point (17, 7) to the circle 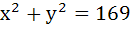 . .
Statement 1 – The tangents are mutually perpendicular, because Statement 2 – The locus of points from which mutually perpendicular tangents are drawn to the given circle is 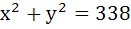 . . The question contains statement – 1 (assertion) and statement 2 (reason). Of these statements mark correct choice if a) Statement 1 and 2 are true. Statement 2 is a correct explanation for statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation for statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true
Tangents are drawn from the point (17, 7) to the circle 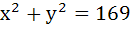 . .
Statement 1 – The tangents are mutually perpendicular, because Statement 2 – The locus of points from which mutually perpendicular tangents are drawn to the given circle is 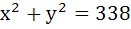 . . The question contains statement – 1 (assertion) and statement 2 (reason). Of these statements mark correct choice if a) Statement 1 and 2 are true. Statement 2 is a correct explanation for statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation for statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true
|
IIT 2007 |
|
|
962 |
Let 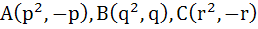 be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. a) 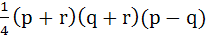 b) 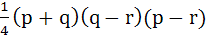 c) 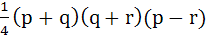 d) 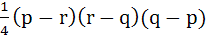
Let 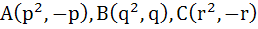 be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. a) 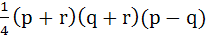 b) 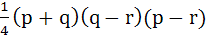 c) 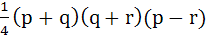 d) 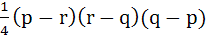
|
IIT 1986 |
|
|
963 |
Two rays in the first quadrant x + y = |a| and ax – y = 1 intersect each other in the interval a ε (a0, ∞). The value of a0 is
Two rays in the first quadrant x + y = |a| and ax – y = 1 intersect each other in the interval a ε (a0, ∞). The value of a0 is
|
IIT 2006 |
|
|
964 |
Find the area of the region bounded by the curve C: y = tanx, tangent drawn to C at 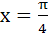 and the X–axis. and the X–axis. a) ln2 – 1 b) 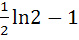 c) 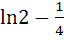 d) 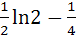
Find the area of the region bounded by the curve C: y = tanx, tangent drawn to C at 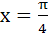 and the X–axis. and the X–axis. a) ln2 – 1 b) 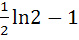 c) 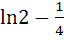 d) 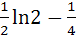
|
IIT 1988 |
|
|
965 |
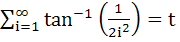 then tan t = then tan t =
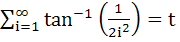 then tan t = then tan t =
|
IIT 2006 |
|
|
966 |
Sketch the curves and identify the region bounded by
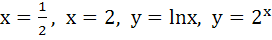
Sketch the curves and identify the region bounded by
|
IIT 1991 |
|
|
967 |
Consider the following linear equations
ax + by + cz = 0
bx + cy + az = 0
cx + ay + bz = 0
Match the statements/expressions in column 1 with column 2
| Column 1 | Column2 | | i. a + b + c ≠ 0 and a2 + b2 + c2 = ab + bc + ca | A. Equations represent planes meeting at only one single point | | ii. a + b + c = 0 and a2 + b2 + c2 ≠ ab + bc + ca | B. The equations represent the line x = y = z | | iii. a + b + c ≠ 0 and a2 + b2 + c2 ≠ ab + bc + ca | C. The equations represent identical planes | | iv. a + b + c = 0 and a2 + b2 + c2 = ab + bc + ca | D.The equations represent the whole of the three dimensional space |
Consider the following linear equations
ax + by + cz = 0
bx + cy + az = 0
cx + ay + bz = 0
Match the statements/expressions in column 1 with column 2
| Column 1 | Column2 | | i. a + b + c ≠ 0 and a2 + b2 + c2 = ab + bc + ca | A. Equations represent planes meeting at only one single point | | ii. a + b + c = 0 and a2 + b2 + c2 ≠ ab + bc + ca | B. The equations represent the line x = y = z | | iii. a + b + c ≠ 0 and a2 + b2 + c2 ≠ ab + bc + ca | C. The equations represent identical planes | | iv. a + b + c = 0 and a2 + b2 + c2 = ab + bc + ca | D.The equations represent the whole of the three dimensional space |
|
IIT 2007 |
|
|
968 |
The domain of the function y(x) given by the equation 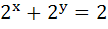 is is a) 0 < x ≤ 1 b) 0 ≤ x ≤ 1 c) 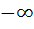 < x ≤ 0 < x ≤ 0 d) 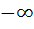 < x < 1 < x < 1
The domain of the function y(x) given by the equation 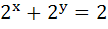 is is a) 0 < x ≤ 1 b) 0 ≤ x ≤ 1 c) 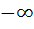 < x ≤ 0 < x ≤ 0 d) 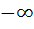 < x < 1 < x < 1
|
IIT 2000 |
|
|
969 |
If A =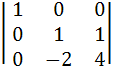 , 6A-1 = A2 + cA + dI , 6A-1 = A2 + cA + dI then (c, d ) is a) (−11, 6) b) (−6, 11) c) (6, 11 ) d) (11, 6 )
If A =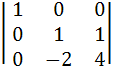 , 6A-1 = A2 + cA + dI , 6A-1 = A2 + cA + dI then (c, d ) is a) (−11, 6) b) (−6, 11) c) (6, 11 ) d) (11, 6 )
|
IIT 2005 |
|
|
970 |
Prove that 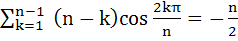
Prove that 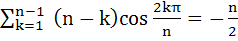
|
IIT 1997 |
|
|
971 |
Tangent at a point P1 (other than (10, 0)) on the curve y = x3 meets the curve again at P2. The tangent at P2 meets the curve at P3 and so on. Show that the abscissae of P1, P2, P3, . . . , Pn form a Geometric Progression. Also find the ratio 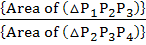 . . a) 32 b) 16 c) 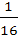 d) 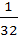
Tangent at a point P1 (other than (10, 0)) on the curve y = x3 meets the curve again at P2. The tangent at P2 meets the curve at P3 and so on. Show that the abscissae of P1, P2, P3, . . . , Pn form a Geometric Progression. Also find the ratio 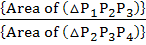 . . a) 32 b) 16 c) 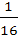 d) 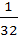
|
IIT 1993 |
|
|
972 |
In what ratio does the X–axis divide the area of the region bounded by the parabolas y = 4x – x2 and y = x2 – x a) 1:4 b) 21:1 c) 21:4 d) 3:4
In what ratio does the X–axis divide the area of the region bounded by the parabolas y = 4x – x2 and y = x2 – x a) 1:4 b) 21:1 c) 21:4 d) 3:4
|
IIT 1994 |
|
|
973 |
Let C1 and C2, be respectively, the parabolas 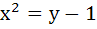 and and 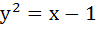 . Let P be any point on C1 and Q be any point on C2. Let P1 and Q1 be the reflections of P and Q respectively with respect to y = x . Prove that P1 lies on C2 and Q1 lies on C1 and . Let P be any point on C1 and Q be any point on C2. Let P1 and Q1 be the reflections of P and Q respectively with respect to y = x . Prove that P1 lies on C2 and Q1 lies on C1 and 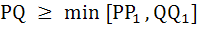 . Hence or otherwise determine points P2 and Q2 on the parabolas C1 and C2 respectively such that . Hence or otherwise determine points P2 and Q2 on the parabolas C1 and C2 respectively such that 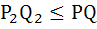 for all points (P, Q) with P on C1 and Q on C2 . for all points (P, Q) with P on C1 and Q on C2 .
|
IIT 2000 |
|
|
974 |
Suppose 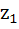 , , 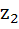 , , 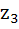 are the vertices of an equilateral triangle inscribed in the circle are the vertices of an equilateral triangle inscribed in the circle 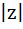 = 2. If = 2. If 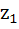 = 1 + i = 1 + i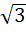 , then find , then find 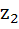 and and 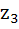 . . a) 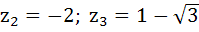 b) 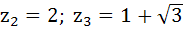 c) 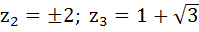 d) None of the above
|
IIT 1994 |
|
|
975 |
A curve y = f(x) passes through the point P:(1, 1). The equation to the normal at (1, 1) to the curve y = f(x) is (x – 1) + a(y – 1) = 0 and the slope of the tangent at any point on the curve is proportional to the ordinate of the point. Determine the equation of the curve. Also obtain the area bounded by the Y–axis, the curve and the normal at P. a) 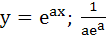 b) y = 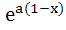 ; ;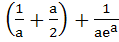 c) 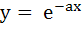 ; ;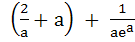 d) 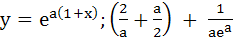
A curve y = f(x) passes through the point P:(1, 1). The equation to the normal at (1, 1) to the curve y = f(x) is (x – 1) + a(y – 1) = 0 and the slope of the tangent at any point on the curve is proportional to the ordinate of the point. Determine the equation of the curve. Also obtain the area bounded by the Y–axis, the curve and the normal at P. a) 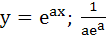 b) y = 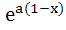 ; ;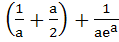 c) 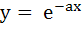 ; ;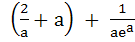 d) 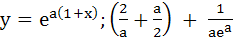
|
IIT 1996 |
|