|
876 |
Domain of definition of the function 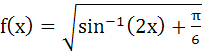 for real values of x is for real values of x is a) 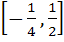 b) 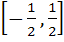 c) 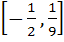 d) 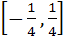
Domain of definition of the function 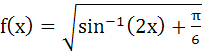 for real values of x is for real values of x is a) 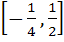 b) 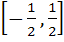 c) 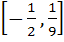 d) 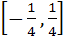
|
IIT 2003 |
|
|
877 |
Let λ and α be real. Find the set of all values of λ for which the system of linear equations
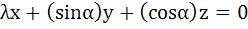
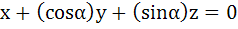
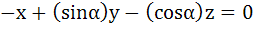
has a non-trivial solution. For λ = 1 find the value of α.
|
IIT 1993 |
|
|
878 |
Let f be a one–one function with domain {x, y, z} and range {1, 2, 3}. It is given that exactly one of the following statements is true and remaining statements are false f (1) = 1, f (y) ≠ 1, f (z) ≠ 2. Determine 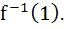
Let f be a one–one function with domain {x, y, z} and range {1, 2, 3}. It is given that exactly one of the following statements is true and remaining statements are false f (1) = 1, f (y) ≠ 1, f (z) ≠ 2. Determine 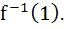
|
IIT 1982 |
|
|
879 |
The value of 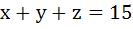 . Given that a, x, y, z, b are in Arithmetic Progression while the value of . Given that a, x, y, z, b are in Arithmetic Progression while the value of 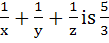 . If a, x, y, z, b are in Harmonic Progression then find a and b. . If a, x, y, z, b are in Harmonic Progression then find a and b.
The value of 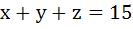 . Given that a, x, y, z, b are in Arithmetic Progression while the value of . Given that a, x, y, z, b are in Arithmetic Progression while the value of 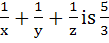 . If a, x, y, z, b are in Harmonic Progression then find a and b. . If a, x, y, z, b are in Harmonic Progression then find a and b.
|
IIT 1978 |
|
|
880 |
Let {x} and [x] denote the fractional and integral part of a real number x respectively. Solve 4{x} = x + [x]
Let {x} and [x] denote the fractional and integral part of a real number x respectively. Solve 4{x} = x + [x]
|
IIT 1994 |
|
|
881 |
If S1, S2, . . . .,Sn are the sums of infinite geometric series whose first terms are 1, 2, 3, . . ., n and whose common ratios are 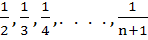 respectively, then find the value of respectively, then find the value of 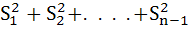
If S1, S2, . . . .,Sn are the sums of infinite geometric series whose first terms are 1, 2, 3, . . ., n and whose common ratios are 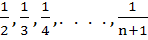 respectively, then find the value of respectively, then find the value of 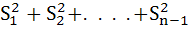
|
IIT 1991 |
|
|
882 |
If 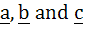 are three non–coplanar vectors, then are three non–coplanar vectors, then 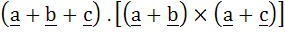 equals equals a) 0 b) 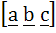 c) 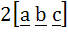 d) 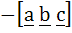
If 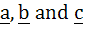 are three non–coplanar vectors, then are three non–coplanar vectors, then 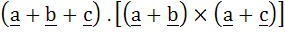 equals equals a) 0 b) 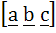 c) 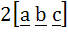 d) 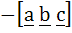
|
IIT 1995 |
|
|
883 |
Let a, b are real positive numbers. If a, A1, A2, b are in Arithmetic Progression, a, G1, G2, b are in Geometric Progression and a, H1, H2, b are in Harmonic Progression show that
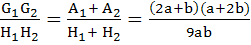
Let a, b are real positive numbers. If a, A1, A2, b are in Arithmetic Progression, a, G1, G2, b are in Geometric Progression and a, H1, H2, b are in Harmonic Progression show that
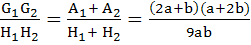
|
IIT 2002 |
|
|
884 |
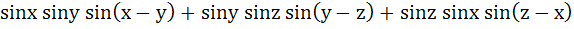 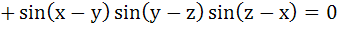
a) True b) False
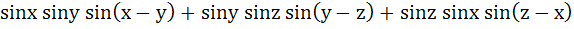 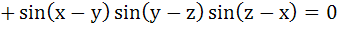
a) True b) False
|
IIT 1978 |
|
|
885 |
Multiple choice Let 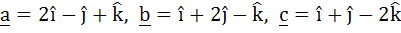 be three vectors. A vector in the plane of b and c whose projection on a is of magnitude be three vectors. A vector in the plane of b and c whose projection on a is of magnitude 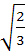 is is a) 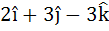 b) 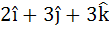 c) 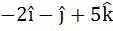 d) 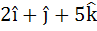
Multiple choice Let 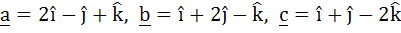 be three vectors. A vector in the plane of b and c whose projection on a is of magnitude be three vectors. A vector in the plane of b and c whose projection on a is of magnitude 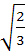 is is a) 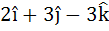 b) 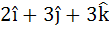 c) 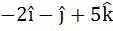 d) 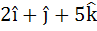
|
IIT 1993 |
|
|
886 |
Let A be vector parallel to the line of intersection of planes P1 and P2. Plane P1 is parallel to the vectors 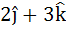 and and 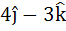 and that P2 is parallel to and that P2 is parallel to 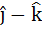 and and 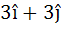 , then the angle between vector A and a given vector , then the angle between vector A and a given vector 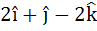 is is a)  b) 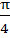 c)  d) 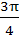
|
IIT 2006 |
|
|
887 |
Find the range of values of t for which 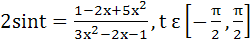 a) (−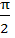 , − , −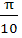 ) ) b) ( 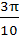 , ,  ) ) c) (− 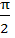 , − , − 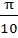 ) U ( ) U ( 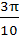 , ,  ) ) d) (−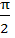 , , 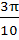 ) )
|
IIT 2005 |
|
|
888 |
A vector A has components A1, A2, A3 in a right handed rectangular cartesian coordinate system OXYZ. The coordinate system is rotated about the X–axis through an angle  . Find the components of A in the new co-ordinate system in terms of A1, A2, A3. . Find the components of A in the new co-ordinate system in terms of A1, A2, A3.
A vector A has components A1, A2, A3 in a right handed rectangular cartesian coordinate system OXYZ. The coordinate system is rotated about the X–axis through an angle  . Find the components of A in the new co-ordinate system in terms of A1, A2, A3. . Find the components of A in the new co-ordinate system in terms of A1, A2, A3.
|
IIT 1983 |
|
|
889 |
The value of 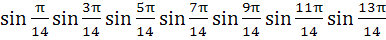 is equal to is equal to a)  b) 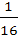 c) 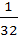 d) 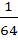
The value of 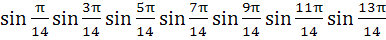 is equal to is equal to a)  b) 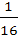 c) 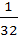 d) 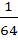
|
IIT 1991 |
|
|
890 |
In a triangle OAB, E is the midpoint of BO and D is a point on AB such that AD : DB = 2 : 1. If OD and AE intercept at P determine the ratio OP : PD using vector methods.
In a triangle OAB, E is the midpoint of BO and D is a point on AB such that AD : DB = 2 : 1. If OD and AE intercept at P determine the ratio OP : PD using vector methods.
|
IIT 1989 |
|
|
891 |
The position vectors of the vertices A, B, C of a tetrahedron are 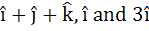 respectively. The altitude from the vertex D to the opposite face ABC meets the median line through A of the triangle ABC at E. If the length of the side AD is 4 and the volume of the tetrahedron is respectively. The altitude from the vertex D to the opposite face ABC meets the median line through A of the triangle ABC at E. If the length of the side AD is 4 and the volume of the tetrahedron is 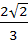 . Find the position vector of E or all possible positions. . Find the position vector of E or all possible positions.
The position vectors of the vertices A, B, C of a tetrahedron are 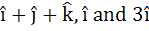 respectively. The altitude from the vertex D to the opposite face ABC meets the median line through A of the triangle ABC at E. If the length of the side AD is 4 and the volume of the tetrahedron is respectively. The altitude from the vertex D to the opposite face ABC meets the median line through A of the triangle ABC at E. If the length of the side AD is 4 and the volume of the tetrahedron is 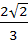 . Find the position vector of E or all possible positions. . Find the position vector of E or all possible positions.
|
IIT 1996 |
|
|
892 |
If 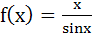 and and 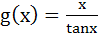 where 0 < x ≤1, then in this interval where 0 < x ≤1, then in this interval a) Both f (x) and g (x) are increasing functions b) Both f (x) and g (x) are decreasing functions c) f (x) is an increasing function d) g (x) is an increasing function
If 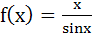 and and 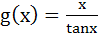 where 0 < x ≤1, then in this interval where 0 < x ≤1, then in this interval a) Both f (x) and g (x) are increasing functions b) Both f (x) and g (x) are decreasing functions c) f (x) is an increasing function d) g (x) is an increasing function
|
IIT 1997 |
|
|
893 |
The number of common tangents to the circles x2 + y2 – 4x − 6y – 12 = 0 and x2 + y2 + 6x + 18y + 26 = 0 is a) 1 b) 2 c) 3 d) 4
The number of common tangents to the circles x2 + y2 – 4x − 6y – 12 = 0 and x2 + y2 + 6x + 18y + 26 = 0 is a) 1 b) 2 c) 3 d) 4
|
IIT 2015 |
|
|
894 |
Let p ≥ 3 be an integer and α, β be the roots of x2 – (p + 1) x + 1 = 0. Using mathematical induction show that αn + βn
i) is an integer
ii) and is not divisible by p.
Let p ≥ 3 be an integer and α, β be the roots of x2 – (p + 1) x + 1 = 0. Using mathematical induction show that αn + βn
i) is an integer
ii) and is not divisible by p.
|
IIT 1992 |
|
|
895 |
The function 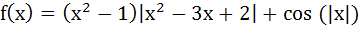 is not differentiable at is not differentiable at a) – 1 b) 0 c) 1 d) 2
The function 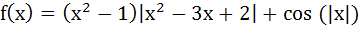 is not differentiable at is not differentiable at a) – 1 b) 0 c) 1 d) 2
|
IIT 1999 |
|
|
896 |
One or more than one correct option Let RS be a diameter of the circle x2 + y2 = 1 where S is the point (1, 0). Let P be a variable point (other than R and S) on the circle and the tangents to the circle at S and P meet at the point Q. The normal to the circle at P intersect a line drawn through Q parallel to RS at a point E. Then the locus of E passes through the point(s) a) b) c) d)
One or more than one correct option Let RS be a diameter of the circle x2 + y2 = 1 where S is the point (1, 0). Let P be a variable point (other than R and S) on the circle and the tangents to the circle at S and P meet at the point Q. The normal to the circle at P intersect a line drawn through Q parallel to RS at a point E. Then the locus of E passes through the point(s) a) b) c) d)
|
IIT 2016 |
|
|
897 |
If x is not an integral multiple of 2π use mathematical induction to prove that
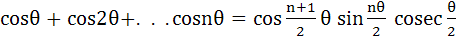
If x is not an integral multiple of 2π use mathematical induction to prove that
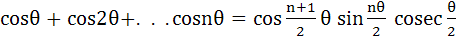
|
IIT 1994 |
|
|
898 |
A circle passing through (1, −2) and touching the axis of X at (3, 0) also passes through the point a) (−5, 2) b) (2, −5) c) (5, −2) d) (−2, 5)
A circle passing through (1, −2) and touching the axis of X at (3, 0) also passes through the point a) (−5, 2) b) (2, −5) c) (5, −2) d) (−2, 5)
|
IIT 2013 |
|
|
899 |
The circles 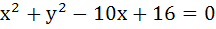 and and 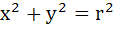 intersect each other in distinct points if intersect each other in distinct points if a) r < 2 b) r > 8 c) 2 < r < 8 d) 2 ≤ r ≤ 8
The circles 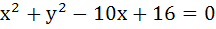 and and 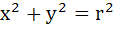 intersect each other in distinct points if intersect each other in distinct points if a) r < 2 b) r > 8 c) 2 < r < 8 d) 2 ≤ r ≤ 8
|
IIT 1994 |
|
|
900 |
Prove by induction that
Pn = Aαn + Bβn for all n ≥ 1
Where α and β are roots of the quadratic equation
x2 – (1 – P) x – P (1 – P) = 0,
P1 = 1, P2 = 1 – P2, . . .,
Pn = (1 – P) Pn – 1 + P (1 – P) Pn – 2 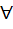 n ≥ 3, n ≥ 3,
and 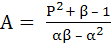 , , 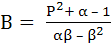
|
IIT 2000 |
|