|
851 |
Determine the smallest positive value of x (in degrees) for which 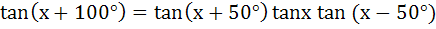 a) 30° b) 50° c) 55° d) 60°
Determine the smallest positive value of x (in degrees) for which 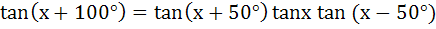 a) 30° b) 50° c) 55° d) 60°
|
IIT 1993 |
|
|
852 |
The real roots of the equation 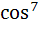 x + x + 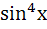 = 1 in the interval (−π, π) are …........... = 1 in the interval (−π, π) are …........... a) x = 0 b) x = ±  c) x = 0 , x = ± 
The real roots of the equation 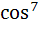 x + x + 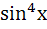 = 1 in the interval (−π, π) are …........... = 1 in the interval (−π, π) are …........... a) x = 0 b) x = ±  c) x = 0 , x = ± 
|
IIT 1997 |
|
|
853 |
The domain of the derivative of the function
f (x) =  a) R  { 0 } { 0 } b) R  c) R  d) R 
The domain of the derivative of the function
f (x) =  a) R  { 0 } { 0 } b) R  c) R  d) R 
|
IIT 2002 |
|
|
854 |
The greater of the two angles
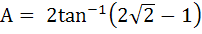 and and 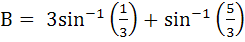 is is a) A b) B c) Both are equal
The greater of the two angles
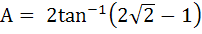 and and 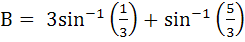 is is a) A b) B c) Both are equal
|
IIT 1989 |
|
|
855 |
If f (x) = sinx + cosx, g (x) = x2 – 1 then g ( f (x)) is invertible in the domain a)  b)  c)  d) 
If f (x) = sinx + cosx, g (x) = x2 – 1 then g ( f (x)) is invertible in the domain a)  b)  c)  d) 
|
IIT 2004 |
|
|
856 |
One or more correct answers
In a triangle the length of the two larger sides are 10 and 9 respectively. If the angles are in arithmetic progression then the length of the third side can be a) 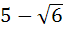 b) 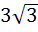 c) 5 d) 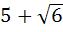 e) None of these
One or more correct answers
In a triangle the length of the two larger sides are 10 and 9 respectively. If the angles are in arithmetic progression then the length of the third side can be a) 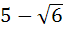 b) 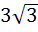 c) 5 d) 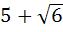 e) None of these
|
IIT 1987 |
|
|
857 |
Let f (x) = Ax2 + Bx + C where A, B , C are real numbers. Prove that if f (x) is an integer then the numbers 2A, A + B and C are all integers. Conversely prove that if the numbers 2A, A + B and C are all integers then f ( x ) is an integer whenever x is an integer.
Let f (x) = Ax2 + Bx + C where A, B , C are real numbers. Prove that if f (x) is an integer then the numbers 2A, A + B and C are all integers. Conversely prove that if the numbers 2A, A + B and C are all integers then f ( x ) is an integer whenever x is an integer.
|
IIT 1998 |
|
|
858 |
A ladder rests against a wall at an angle α to the horizontal. If its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal, then 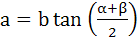 . . a) True b) False
A ladder rests against a wall at an angle α to the horizontal. If its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal, then 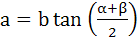 . . a) True b) False
|
IIT 1985 |
|
|
859 |
Let  be the vertices of an n sided regular polygon such that be the vertices of an n sided regular polygon such that 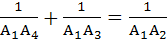 . Then find n. . Then find n. a) 5 b) 6 c) 7 d) 8
Let  be the vertices of an n sided regular polygon such that be the vertices of an n sided regular polygon such that 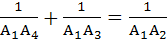 . Then find n. . Then find n. a) 5 b) 6 c) 7 d) 8
|
IIT 1994 |
|
|
860 |
A variable plane at a distance of one unit from the origin cuts the coordinate axes at A, B and C. If the centroid D(x, y, z) of triangle ABC satisfies the relation 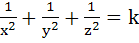 then the value of k is then the value of k is a) 9 b)  c) 1 d) 3
A variable plane at a distance of one unit from the origin cuts the coordinate axes at A, B and C. If the centroid D(x, y, z) of triangle ABC satisfies the relation 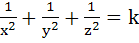 then the value of k is then the value of k is a) 9 b)  c) 1 d) 3
|
IIT 2005 |
|
|
861 |
Find the equation of the plane passing through the points (2, 1, 0), (4, 1, 1), (5, 0, 1). Find the point Q such that its distance from the plane is equal to the point P(2, 1, 6) from the plane and the line joining P and Q is perpendicular to the plane.
Find the equation of the plane passing through the points (2, 1, 0), (4, 1, 1), (5, 0, 1). Find the point Q such that its distance from the plane is equal to the point P(2, 1, 6) from the plane and the line joining P and Q is perpendicular to the plane.
|
IIT 2003 |
|
|
862 |
The unit vector perpendicular to the plane determined by
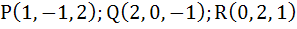 is. is.
The unit vector perpendicular to the plane determined by
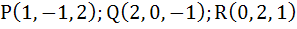 is. is.
|
IIT 1983 |
|
|
863 |
Consider the lines 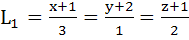 ; ;
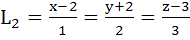
The shortest distance between L1 and L2 is
a) 0 b) 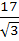 c) 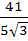 d) 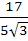
Consider the lines 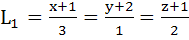 ; ;
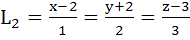
The shortest distance between L1 and L2 is
a) 0 b) 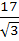 c) 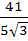 d) 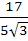
|
IIT 2008 |
|
|
864 |
Let ABCD is the base of parallelopiped T and Aʹ.BʹCʹDʹ be the upper face. The parallelopiped is compressed so that the vertex Aʹ shifts to Aʹʹ on a parallelepiped S. If the volume of the new parallelopiped is 90% of the parallelopiped T, prove that the locus of Aʹʹ is a plane.
Let ABCD is the base of parallelopiped T and Aʹ.BʹCʹDʹ be the upper face. The parallelopiped is compressed so that the vertex Aʹ shifts to Aʹʹ on a parallelepiped S. If the volume of the new parallelopiped is 90% of the parallelopiped T, prove that the locus of Aʹʹ is a plane.
|
IIT 2004 |
|
|
865 |
Show that 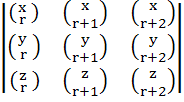 = = 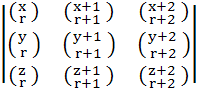
Show that 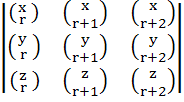 = = 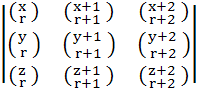
|
IIT 1985 |
|
|
866 |
For all A, B, C, P, Q, R show that
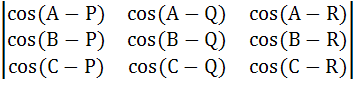 = 0 = 0
For all A, B, C, P, Q, R show that
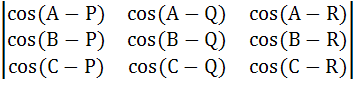 = 0 = 0
|
IIT 1996 |
|
|
867 |
Let f(x) = |x – 1|, then a) 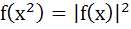 b) 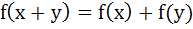 c) 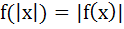 d) None of these
Let f(x) = |x – 1|, then a) 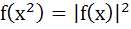 b) 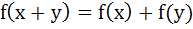 c) 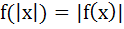 d) None of these
|
IIT 1983 |
|
|
868 |
The differential equation representing the family of curves 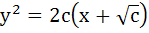 where c is a positive parameter, is of where c is a positive parameter, is of a) Order 1 b) Order 2 c) Degree 3 d) Degree 4
The differential equation representing the family of curves 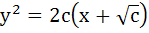 where c is a positive parameter, is of where c is a positive parameter, is of a) Order 1 b) Order 2 c) Degree 3 d) Degree 4
|
IIT 1999 |
|
|
869 |
Let a, b, c be real numbers with a2 + b2 + c2 = 1. Show that the equation represents a straight line
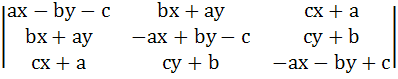 = 0 = 0
Let a, b, c be real numbers with a2 + b2 + c2 = 1. Show that the equation represents a straight line
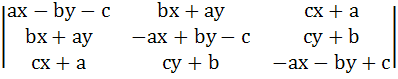 = 0 = 0
|
IIT 2001 |
|
|
870 |
Let 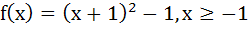 , then the set , then the set 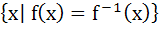 is is a) 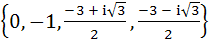 b) 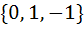 c) 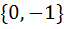 d) ϕ
Let 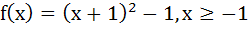 , then the set , then the set 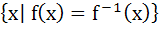 is is a) 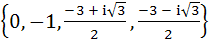 b) 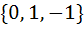 c) 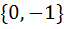 d) ϕ
|
IIT 1995 |
|
|
871 |
A normal is drawn at a point 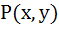 of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is 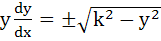
A normal is drawn at a point 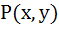 of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is 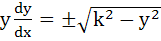
|
IIT 1994 |
|
|
872 |
If f(x) = 3x – 5 then 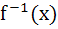 a) is given by 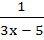 b) is given by 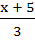 c) does not exist because f is not one-one d) does not exist because f is not onto
If f(x) = 3x – 5 then 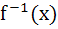 a) is given by 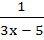 b) is given by 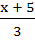 c) does not exist because f is not one-one d) does not exist because f is not onto
|
IIT 1998 |
|
|
873 |
Find the integral solutions of the following system of inequality
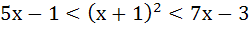 a) x = 1 b) x = 2 c) x = 3 d) x = 4
Find the integral solutions of the following system of inequality
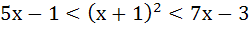 a) x = 1 b) x = 2 c) x = 3 d) x = 4
|
IIT 1979 |
|
|
874 |
Area bounded by 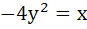 and and 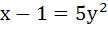
Area bounded by 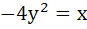 and and 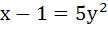
|
IIT 2006 |
|
|
875 |
mn squares of equal size are arranged to form a rectangle of dimension m by n, where m and n are natural numbers. Two squares will be called neighbours if they have exactly one common side. A natural number is written in each square such that the number written in any square is the arithmetic mean of the numbers written in the neighbouring squares. Show that this is possible only if all the numbers used are equal.
mn squares of equal size are arranged to form a rectangle of dimension m by n, where m and n are natural numbers. Two squares will be called neighbours if they have exactly one common side. A natural number is written in each square such that the number written in any square is the arithmetic mean of the numbers written in the neighbouring squares. Show that this is possible only if all the numbers used are equal.
|
IIT 1982 |
|