|
801 |
Let O (0, 0), P (3, 4), Q (6, 0) be the vertices of the triangle OPQ. The point inside the triangle OPQ is such that OPR, PQR, OQR are of equal area. The coordinates of R are a) 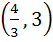 b) 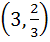 c) 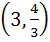 d) 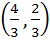
Let O (0, 0), P (3, 4), Q (6, 0) be the vertices of the triangle OPQ. The point inside the triangle OPQ is such that OPR, PQR, OQR are of equal area. The coordinates of R are a) 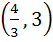 b) 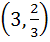 c) 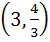 d) 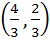
|
IIT 2006 |
|
|
802 |
If f be a one–one function with domain { x, y, z}and range { 1, 2, 3}. It is given that exactly one of the following statements is true and the remaining statements are false. Determine 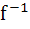 (1) (1) 1. f(x) = 1 2. f(y) ≠ 1 3. f(z) ≠ 2 a) {0} b) {1} c) {y} d) none of the above
If f be a one–one function with domain { x, y, z}and range { 1, 2, 3}. It is given that exactly one of the following statements is true and the remaining statements are false. Determine 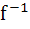 (1) (1) 1. f(x) = 1 2. f(y) ≠ 1 3. f(z) ≠ 2 a) {0} b) {1} c) {y} d) none of the above
|
IIT 1982 |
|
|
803 |
One or more correct answers
In triangle ABC the internal angle bisector of ∠A meets the side BC in D. DE is a perpendicular to AD which meets AC in E and AB in F. Then a) AE is harmonic mean of b and c b) AD 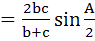 c) 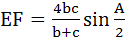 d) Δ AEF is isosceles
One or more correct answers
In triangle ABC the internal angle bisector of ∠A meets the side BC in D. DE is a perpendicular to AD which meets AC in E and AB in F. Then a) AE is harmonic mean of b and c b) AD 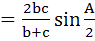 c) 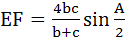 d) Δ AEF is isosceles
|
IIT 2006 |
|
|
804 |
For a triangle ABC it is given that 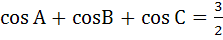 , then Δ ABC is equilateral. , then Δ ABC is equilateral. a) True b) False
For a triangle ABC it is given that 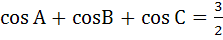 , then Δ ABC is equilateral. , then Δ ABC is equilateral. a) True b) False
|
IIT 1984 |
|
|
805 |
True / False The function f (x) = 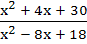 is not one to one. is not one to one. a) True b) False
True / False The function f (x) = 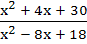 is not one to one. is not one to one. a) True b) False
|
IIT 1983 |
|
|
806 |
Find the set of all values of a such that 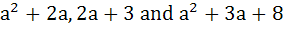 are sides of a triangle. are sides of a triangle. a) (0, 3) b) (3, ∞) c) (0, 5) d) (5, ∞)
Find the set of all values of a such that 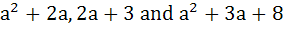 are sides of a triangle. are sides of a triangle. a) (0, 3) b) (3, ∞) c) (0, 5) d) (5, ∞)
|
IIT 1985 |
|
|
807 |
Fill in the blank Let A be the set of n distinct elements then the total number of distinct functions from A to A is ……… and out of these …… are onto a) n!, 1 b) nn, n! c) nn, 1 d) none of the above
Fill in the blank Let A be the set of n distinct elements then the total number of distinct functions from A to A is ……… and out of these …… are onto a) n!, 1 b) nn, n! c) nn, 1 d) none of the above
|
IIT 1985 |
|
|
808 |
In a triangle of base a the ratio of the other two sides is r (< 1). Then the altitude of the triangle is less than or equal to 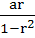 . . a) True b) False
In a triangle of base a the ratio of the other two sides is r (< 1). Then the altitude of the triangle is less than or equal to 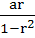 . . a) True b) False
|
IIT 1991 |
|
|
809 |
The value of k such that 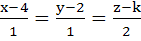 lies in the plane lies in the plane
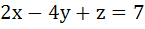 is is a) 7 b) – 7 c) No real value d) 4
The value of k such that 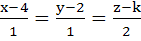 lies in the plane lies in the plane
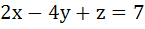 is is a) 7 b) – 7 c) No real value d) 4
|
IIT 2003 |
|
|
810 |
If ABCD are four points in a space, prove that
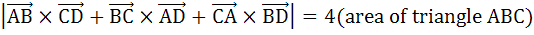
If ABCD are four points in a space, prove that
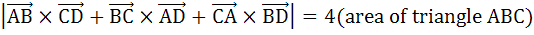
|
IIT 1987 |
|
|
811 |
If a, b, c are distinct positive numbers then the expression
( b + c – a ) ( c + a – b ) ( a + b – c ) –abc is a) Positive b) Negative c) Non–positive d) None of these
If a, b, c are distinct positive numbers then the expression
( b + c – a ) ( c + a – b ) ( a + b – c ) –abc is a) Positive b) Negative c) Non–positive d) None of these
|
IIT 1986 |
|
|
812 |
Let A and B be square matrices of equal degree, then which one is correct amongst the following a) A + B = B + A b) A + B = A – B c) A – B = B – A d) AB = BA
Let A and B be square matrices of equal degree, then which one is correct amongst the following a) A + B = B + A b) A + B = A – B c) A – B = B – A d) AB = BA
|
IIT 1995 |
|
|
813 |
The edges of a parallelepiped are of unit length and are parallel to non-coplanar unit vectors 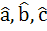 such that such that 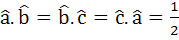 . Then the volume of the parallelepiped is . Then the volume of the parallelepiped is a) 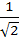 b) 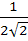 c) 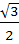 d) 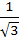
The edges of a parallelepiped are of unit length and are parallel to non-coplanar unit vectors 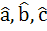 such that such that 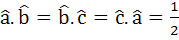 . Then the volume of the parallelepiped is . Then the volume of the parallelepiped is a) 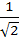 b) 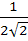 c) 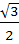 d) 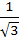
|
IIT 2008 |
|
|
814 |
If P = 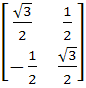 , A = , A = 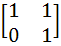 and Q = PAPT and Q = PAPT then PT (Q2005) P is equal to a) 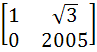 b) 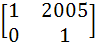 c) 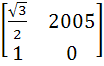 d) 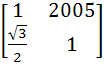
If P = 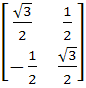 , A = , A = 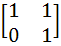 and Q = PAPT and Q = PAPT then PT (Q2005) P is equal to a) 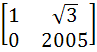 b) 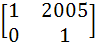 c) 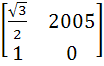 d) 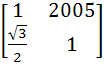
|
IIT 2005 |
|
|
815 |
Consider three planes
P1 : x – y + z = 1 P2 : x + y – z = −1 P3 : x – 3y + 3z = 2 Let L1, L2, L3 be lines of intersection of planes P2 and P3, P3 and P1, and P1 and P2 respectively. Statement 1 – At least two of the lines L1, L2, L3 are non parallel Statement 2 – The three planes do not have a common point. a) Statement 1 is true. Statement 2 is true. Statement 2 is a correct explanation of statement 1. b) Statement 1 is true. Statement 2 is true. Statement 2 is not a correct explanation of statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
Consider three planes
P1 : x – y + z = 1 P2 : x + y – z = −1 P3 : x – 3y + 3z = 2 Let L1, L2, L3 be lines of intersection of planes P2 and P3, P3 and P1, and P1 and P2 respectively. Statement 1 – At least two of the lines L1, L2, L3 are non parallel Statement 2 – The three planes do not have a common point. a) Statement 1 is true. Statement 2 is true. Statement 2 is a correct explanation of statement 1. b) Statement 1 is true. Statement 2 is true. Statement 2 is not a correct explanation of statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
|
IIT 2008 |
|
|
816 |
Show that the system of equations
3x – y + 4z = 3
x + 2y − 3z = −2
6x + 5y + λz = −3
has at least one solution for any real number λ ≠ −5. Find the set of solutions if λ = −5 a) 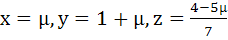 b) 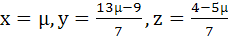 c) 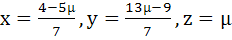 d) 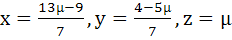
Show that the system of equations
3x – y + 4z = 3
x + 2y − 3z = −2
6x + 5y + λz = −3
has at least one solution for any real number λ ≠ −5. Find the set of solutions if λ = −5 a) 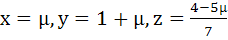 b) 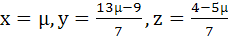 c) 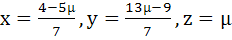 d) 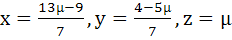
|
IIT 1983 |
|
|
817 |
The solution of primitive equation
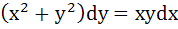 is is 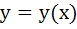 . If . If 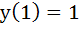 and and 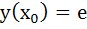 then then 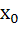 is is a) 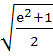 b) 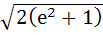 c) 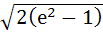 d) 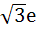
|
IIT 2005 |
|
|
818 |
If 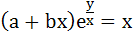 then prove that then prove that 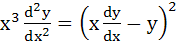
If 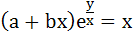 then prove that then prove that 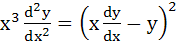
|
IIT 1983 |
|
|
819 |
If M is a 3 x 3 matrix where det (M) = 1 and MMT = I, then prove that det (M – I) = 0.
If M is a 3 x 3 matrix where det (M) = 1 and MMT = I, then prove that det (M – I) = 0.
|
IIT 2004 |
|
|
820 |
Let f(x) be defined for all x > 0 and be continuous. If f(x) satisfies 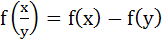 for all x, y and f(e)=1 then for all x, y and f(e)=1 then a) f(x) is bounded b) 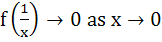 c) x f(x) → 1 as x → 0 d) f(x) = lnx
Let f(x) be defined for all x > 0 and be continuous. If f(x) satisfies 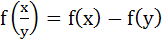 for all x, y and f(e)=1 then for all x, y and f(e)=1 then a) f(x) is bounded b) 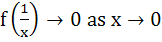 c) x f(x) → 1 as x → 0 d) f(x) = lnx
|
IIT 1995 |
|
|
821 |
The number of values of x where the function 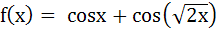 attains its maximum is attains its maximum is a) 0 b) 1 c) 2 d) infinite
The number of values of x where the function 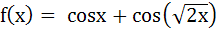 attains its maximum is attains its maximum is a) 0 b) 1 c) 2 d) infinite
|
IIT 1998 |
|
|
822 |
The domain of the definition of the function y given by the equation 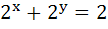 is is a) 0 < x < 1 b) 0 ≤ x ≤ 1 c) 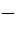 ∞ < x ≤ 0 ∞ < x ≤ 0 d) 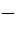 ∞ < x ≤ 1 ∞ < x ≤ 1
The domain of the definition of the function y given by the equation 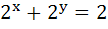 is is a) 0 < x < 1 b) 0 ≤ x ≤ 1 c) 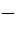 ∞ < x ≤ 0 ∞ < x ≤ 0 d) 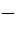 ∞ < x ≤ 1 ∞ < x ≤ 1
|
IIT 2000 |
|
|
823 |
Solution of the differential equation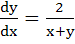 is is
Solution of the differential equation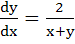 is is
|
IIT 2006 |
|
|
824 |
Let A = 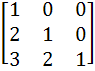 If U1, U2, U3 are column matrices satisfying
AU1 = 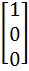 , AU2 = , AU2 = 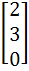 and AU3 = and AU3 = 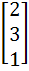 and U is a 3 x 3 matrix whose columns are U1, U2, U3 then the value of [ 3 2 0 ] U 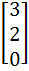 is is a) 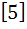 b) 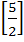 c) 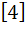 d) 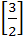
Let A = 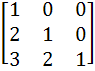 If U1, U2, U3 are column matrices satisfying
AU1 = 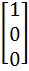 , AU2 = , AU2 = 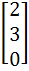 and AU3 = and AU3 = 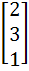 and U is a 3 x 3 matrix whose columns are U1, U2, U3 then the value of [ 3 2 0 ] U 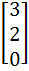 is is a) 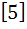 b) 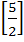 c) 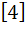 d) 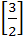
|
IIT 2006 |
|
|
825 |
Let f(x) = 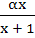 , x ≠ , x ≠ 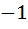 then for what value of α, f(f(x)) = x then for what value of α, f(f(x)) = x a) 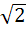 b) 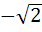 c) 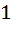 d) 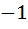
Let f(x) = 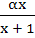 , x ≠ , x ≠ 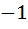 then for what value of α, f(f(x)) = x then for what value of α, f(f(x)) = x a) 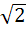 b) 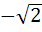 c) 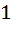 d) 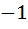
|
IIT 2001 |
|