|
776 |
Let a, b, c, d be real numbers in geometric progression. If u, v, w satisfy the system of equations 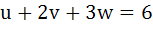
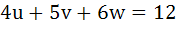
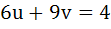
Then show that the roots of the equation
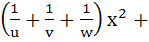
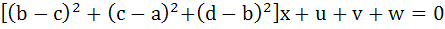
and 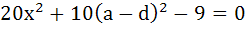 are reciprocal of each other. are reciprocal of each other.
|
IIT 1999 |
|
|
777 |
Subjective Problems
Let f (x + y) = f (x) . f (y) for all x, y. Suppose f (5) = 2 and 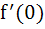 = 3. Find f (5). = 3. Find f (5).
Subjective Problems
Let f (x + y) = f (x) . f (y) for all x, y. Suppose f (5) = 2 and 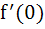 = 3. Find f (5). = 3. Find f (5).
|
IIT 1981 |
|
|
778 |
Find the natural number a for which 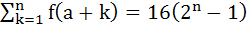 where the function f satisfies the relation f(x + y) = f(x) f(y) for all natural numbers x and y and further f(1) = 2. where the function f satisfies the relation f(x + y) = f(x) f(y) for all natural numbers x and y and further f(1) = 2.
Find the natural number a for which 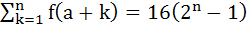 where the function f satisfies the relation f(x + y) = f(x) f(y) for all natural numbers x and y and further f(1) = 2. where the function f satisfies the relation f(x + y) = f(x) f(y) for all natural numbers x and y and further f(1) = 2.
|
IIT 1992 |
|
|
779 |
The interior angles of a polygon are in Arithmetic Progression. The smallest angle is 120° and the common difference is 5. Find the number of sides of the polygon.
The interior angles of a polygon are in Arithmetic Progression. The smallest angle is 120° and the common difference is 5. Find the number of sides of the polygon.
|
IIT 1980 |
|
|
780 |
If 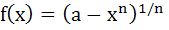 where a > 0 and n is a positive integer then f(f(x)) = x. where a > 0 and n is a positive integer then f(f(x)) = x. a) True b) False
If 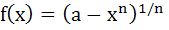 where a > 0 and n is a positive integer then f(f(x)) = x. where a > 0 and n is a positive integer then f(f(x)) = x. a) True b) False
|
IIT 1983 |
|
|
781 |
A vector a has components 2p and 1 with respect to a rectangular cartesian system. This system is rotated through a certain angle about the origin in the counter clockwise sense. If with respect to new system a has components p + 1 and 1 then a) p ≠ 0 b) p = 1 or p = 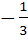 c) p = −1 or 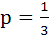 d) p = 1 or p = −1 e) None of these
A vector a has components 2p and 1 with respect to a rectangular cartesian system. This system is rotated through a certain angle about the origin in the counter clockwise sense. If with respect to new system a has components p + 1 and 1 then a) p ≠ 0 b) p = 1 or p = 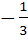 c) p = −1 or 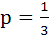 d) p = 1 or p = −1 e) None of these
|
IIT 1986 |
|
|
782 |
The domain of the function 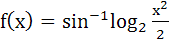 is is
The domain of the function 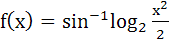 is is
|
IIT 1984 |
|
|
783 |
If f is an even function defined on (−5, 5) then the four real values of x satisfying the equation 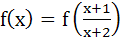 are are
If f is an even function defined on (−5, 5) then the four real values of x satisfying the equation 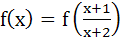 are are
|
IIT 1996 |
|
|
784 |
Let a1, a2, … an be positive real numbers in Geometric Progression. For each n let An, Gn, Hn be respectively the arithmetic mean, geometric mean and harmonic mean of a1, a2, . . . ., an. Find the expressions for the Geometric mean of G1, G2, . . . .Gn in terms of A1, A2, . . . .,An; H1, H2, . . . .Hn
Let a1, a2, … an be positive real numbers in Geometric Progression. For each n let An, Gn, Hn be respectively the arithmetic mean, geometric mean and harmonic mean of a1, a2, . . . ., an. Find the expressions for the Geometric mean of G1, G2, . . . .Gn in terms of A1, A2, . . . .,An; H1, H2, . . . .Hn
|
IIT 2001 |
|
|
785 |
Let 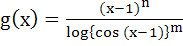 , 0 < x < 2 are integers m ≠ 0, n > 0 and let p be the left hand derivative of |x − 1| at x = 1. If , 0 < x < 2 are integers m ≠ 0, n > 0 and let p be the left hand derivative of |x − 1| at x = 1. If 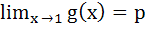 , then , then a) n = −1, m = 1 b) n = 1, m = −1 c) n = 2, m = 2 d) n > 2, n = m
Let 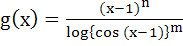 , 0 < x < 2 are integers m ≠ 0, n > 0 and let p be the left hand derivative of |x − 1| at x = 1. If , 0 < x < 2 are integers m ≠ 0, n > 0 and let p be the left hand derivative of |x − 1| at x = 1. If 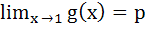 , then , then a) n = −1, m = 1 b) n = 1, m = −1 c) n = 2, m = 2 d) n > 2, n = m
|
IIT 2008 |
|
|
786 |
For three vectors 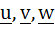 which of the following expressions is not equal to any of the remaining three which of the following expressions is not equal to any of the remaining three a) 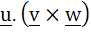 b) 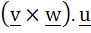 c) 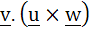 d) 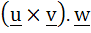
For three vectors 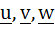 which of the following expressions is not equal to any of the remaining three which of the following expressions is not equal to any of the remaining three a) 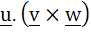 b) 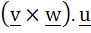 c) 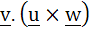 d) 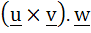
|
IIT 1998 |
|
|
787 |
If total number of runs scored in n matches is
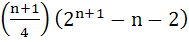 where n > 1 and the runs scored in the kth match are given by k.2n + 1 – k where 1 ≤ k ≤ n. Find n. where n > 1 and the runs scored in the kth match are given by k.2n + 1 – k where 1 ≤ k ≤ n. Find n.
If total number of runs scored in n matches is
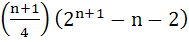 where n > 1 and the runs scored in the kth match are given by k.2n + 1 – k where 1 ≤ k ≤ n. Find n. where n > 1 and the runs scored in the kth match are given by k.2n + 1 – k where 1 ≤ k ≤ n. Find n.
|
IIT 2005 |
|
|
788 |
In a triangle ABC if cotA, cotB, cotC are in Arithmetic Progression then a, b, c are in . . . . . Progression.
In a triangle ABC if cotA, cotB, cotC are in Arithmetic Progression then a, b, c are in . . . . . Progression.
|
IIT 1985 |
|
|
789 |
For any odd integer n ≥ 1,
n3 – (n – 1)3 + . . . + (−)n – 1 13 = . . .
For any odd integer n ≥ 1,
n3 – (n – 1)3 + . . . + (−)n – 1 13 = . . .
|
IIT 1996 |
|
|
790 |
A unit vector which is orthogonal to the vectors 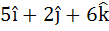 and and coplanar with the vectors 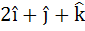 and and 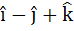 is is a) 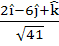 b) 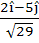 c) 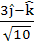 d) 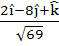
A unit vector which is orthogonal to the vectors 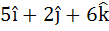 and and coplanar with the vectors 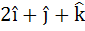 and and 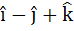 is is a) 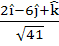 b) 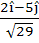 c) 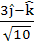 d) 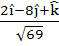
|
IIT 2004 |
|
|
791 |
The area of the equilateral triangle which contains three coins of unit radius is a) 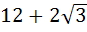 square units square units b) 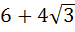 square units square units c) 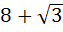 square units square units d) 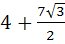 square units square units
The area of the equilateral triangle which contains three coins of unit radius is a) 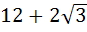 square units square units b) 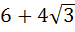 square units square units c) 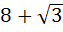 square units square units d) 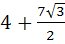 square units square units
|
IIT 2005 |
|
|
792 |
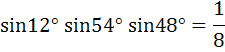
a) True b) False
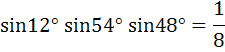
a) True b) False
|
IIT 1982 |
|
|
793 |
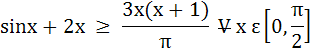
a) True b) False
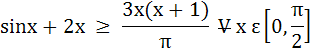
a) True b) False
|
IIT 2004 |
|
|
794 |
Match the following 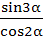 is is | Column 1 | Column 2 | | i) Positive | A) (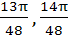 ) ) | | ii) Negative | B) (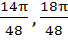 ) ) | | | C) (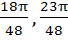 ) ) | | | D) (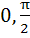 ) ) |
Match the following 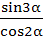 is is | Column 1 | Column 2 | | i) Positive | A) (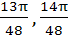 ) ) | | ii) Negative | B) (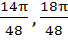 ) ) | | | C) (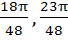 ) ) | | | D) (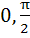 ) ) |
|
IIT 1992 |
|
|
795 |
If the vectors b, c, d, are not coplanar then prove that a is parallel to the vector 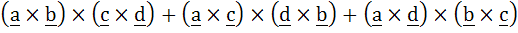
If the vectors b, c, d, are not coplanar then prove that a is parallel to the vector 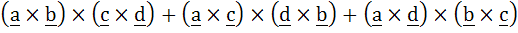
|
IIT 1994 |
|
|
796 |
Prove by vector method or otherwise, that the point of intersection of the diagonals of a trapezium lies on the line passing through the mid points of the parallel sides (you may assume that the trapezium is not a parallelogram)
Prove by vector method or otherwise, that the point of intersection of the diagonals of a trapezium lies on the line passing through the mid points of the parallel sides (you may assume that the trapezium is not a parallelogram)
|
IIT 1998 |
|
|
797 |
True/False If 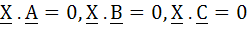 for some non zero vector X then for some non zero vector X then 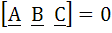 a) True b) False
True/False If 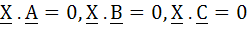 for some non zero vector X then for some non zero vector X then 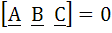 a) True b) False
|
IIT 1983 |
|
|
798 |
If 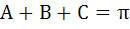 then then 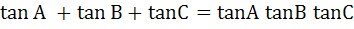 a) True b) False
If 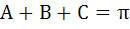 then then 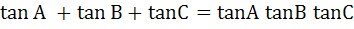 a) True b) False
|
IIT 1979 |
|
|
799 |
Let 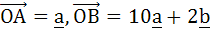 and and 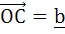 where O, A and B are non-collinear points. Let p denote the area of the quadrilateral OABC and let q denote the area of the quadrilateral with OA and OC as adjacent sides. If p = kq then k = . . . . . where O, A and B are non-collinear points. Let p denote the area of the quadrilateral OABC and let q denote the area of the quadrilateral with OA and OC as adjacent sides. If p = kq then k = . . . . .
Let 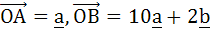 and and 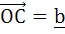 where O, A and B are non-collinear points. Let p denote the area of the quadrilateral OABC and let q denote the area of the quadrilateral with OA and OC as adjacent sides. If p = kq then k = . . . . . where O, A and B are non-collinear points. Let p denote the area of the quadrilateral OABC and let q denote the area of the quadrilateral with OA and OC as adjacent sides. If p = kq then k = . . . . .
|
IIT 1997 |
|
|
800 |
Prove that 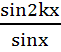 = 2[cosx + cos3x + cos5x + … + cos(2k−1)x] for any positive integer k. Hence prove that = 2[cosx + cos3x + cos5x + … + cos(2k−1)x] for any positive integer k. Hence prove that 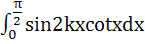 = = 
|
IIT 1990 |
|