|
726 |
If f : [ 1, 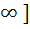 → [ 2, → [ 2, 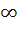 ] is given by f (x) = x + ] is given by f (x) = x +  then then 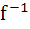 ( x ) is given by ( x ) is given by a) 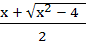 b) 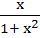 c) 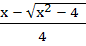 d) 1 + 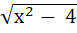
|
IIT 2001 |
|
|
727 |
The function of f : R → R be defined by f (x) = 2x + sinx for x ε R . Then f is a) one-one and onto b) one-one but not onto c) onto but not one-one d) neither one-one nor onto
The function of f : R → R be defined by f (x) = 2x + sinx for x ε R . Then f is a) one-one and onto b) one-one but not onto c) onto but not one-one d) neither one-one nor onto
|
IIT 2002 |
|
|
728 |
Multiple choice There exists a triangle ABC satisfying the conditions a) bsinA = a, A <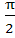 b) bsinA > a, A >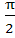 c) bsinA > a, A <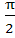 d) bsinA < a, A <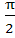 , b > a , b > a e) bsinA < a, A >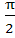 , b = a , b = a
Multiple choice There exists a triangle ABC satisfying the conditions a) bsinA = a, A <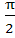 b) bsinA > a, A >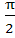 c) bsinA > a, A <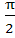 d) bsinA < a, A <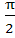 , b > a , b > a e) bsinA < a, A >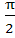 , b = a , b = a
|
IIT 1986 |
|
|
729 |
With usual notation if in a triangle ABC, 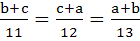 then then 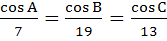 . .
a) True b) False
With usual notation if in a triangle ABC, 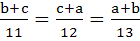 then then 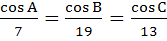 . .
a) True b) False
|
IIT 1984 |
|
|
730 |
If in a triangle ABC, cosA cosB + sinA sinB sin C = 1 then show that a : b : c = 1 : 1 : 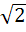 a) True b) False
If in a triangle ABC, cosA cosB + sinA sinB sin C = 1 then show that a : b : c = 1 : 1 : 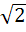 a) True b) False
|
IIT 1986 |
|
|
731 |
If the lines 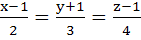 and and 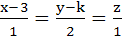 intersect then the value of k is intersect then the value of k is a)  b)  c) 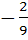 d) 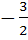
If the lines 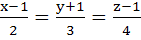 and and 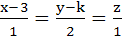 intersect then the value of k is intersect then the value of k is a)  b)  c) 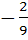 d) 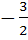
|
IIT 2004 |
|
|
732 |
The area of a triangle whose vertices are
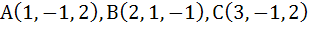 is is
The area of a triangle whose vertices are
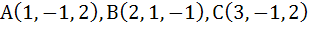 is is
|
IIT 1983 |
|
|
733 |
The parameter on which the value of the determinant
Δ = 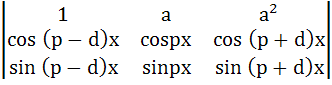
does not depend upon is a) a b) p c) d d) x
The parameter on which the value of the determinant
Δ = 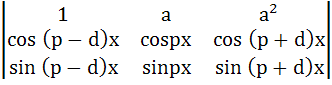
does not depend upon is a) a b) p c) d d) x
|
IIT 1997 |
|
|
734 |
Consider the lines 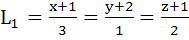 ; ;
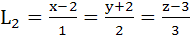
The unit vector perpendicular to both L1 and L2 is
a) 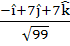 b) 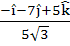 c) 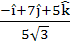 d) 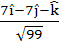
Consider the lines 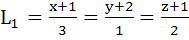 ; ;
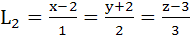
The unit vector perpendicular to both L1 and L2 is
a) 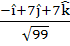 b) 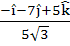 c) 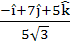 d) 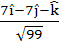
|
IIT 2008 |
|
|
735 |
If b > a then the equation ( x – a ) ( x – b )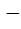 1 = 0 has 1 = 0 has a) Both roots in [ a, b ] b) Both roots in ( 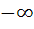 , a ) , a ) c) Both roots in ( 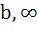 ) ) d) One root in ( 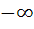 , a ) and other in ( , a ) and other in (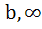 ) )
If b > a then the equation ( x – a ) ( x – b )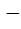 1 = 0 has 1 = 0 has a) Both roots in [ a, b ] b) Both roots in ( 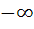 , a ) , a ) c) Both roots in ( 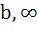 ) ) d) One root in ( 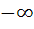 , a ) and other in ( , a ) and other in (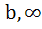 ) )
|
IIT 2000 |
|
|
736 |
For what value of m does the system of equations 3x + my = m, 2x − 5y = 20 have a solution satisfying the condition x > 0, y > 0. a) m 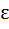 (−∞, ∞) (−∞, ∞) b) m 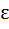 (−∞, −15) ∪ (30, ∞) (−∞, −15) ∪ (30, ∞) c) 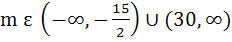 d) 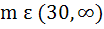
For what value of m does the system of equations 3x + my = m, 2x − 5y = 20 have a solution satisfying the condition x > 0, y > 0. a) m 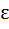 (−∞, ∞) (−∞, ∞) b) m 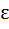 (−∞, −15) ∪ (30, ∞) (−∞, −15) ∪ (30, ∞) c) 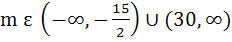 d) 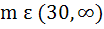
|
IIT 1979 |
|
|
737 |
Show that 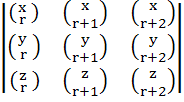 = = 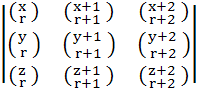
Show that 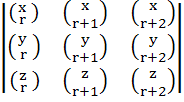 = = 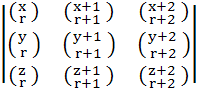
|
IIT 1985 |
|
|
738 |
For all A, B, C, P, Q, R show that
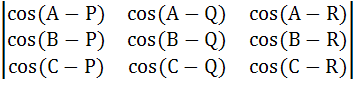 = 0 = 0
For all A, B, C, P, Q, R show that
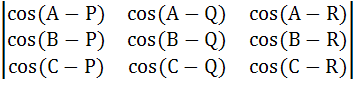 = 0 = 0
|
IIT 1996 |
|
|
739 |
Let f(x) = |x – 1|, then a) 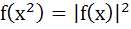 b) 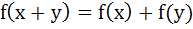 c) 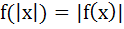 d) None of these
Let f(x) = |x – 1|, then a) 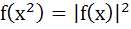 b) 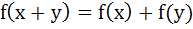 c) 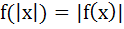 d) None of these
|
IIT 1983 |
|
|
740 |
The differential equation representing the family of curves 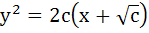 where c is a positive parameter, is of where c is a positive parameter, is of a) Order 1 b) Order 2 c) Degree 3 d) Degree 4
The differential equation representing the family of curves 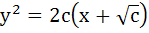 where c is a positive parameter, is of where c is a positive parameter, is of a) Order 1 b) Order 2 c) Degree 3 d) Degree 4
|
IIT 1999 |
|
|
741 |
Let a, b, c be real numbers with a2 + b2 + c2 = 1. Show that the equation represents a straight line
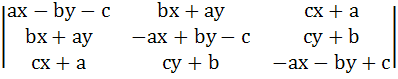 = 0 = 0
Let a, b, c be real numbers with a2 + b2 + c2 = 1. Show that the equation represents a straight line
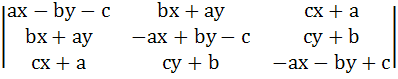 = 0 = 0
|
IIT 2001 |
|
|
742 |
Let 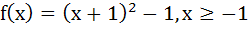 , then the set , then the set 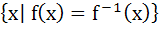 is is a) 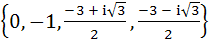 b) 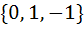 c) 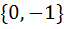 d) ϕ
Let 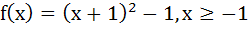 , then the set , then the set 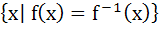 is is a) 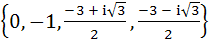 b) 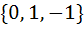 c) 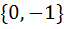 d) ϕ
|
IIT 1995 |
|
|
743 |
A normal is drawn at a point 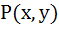 of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is 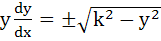
A normal is drawn at a point 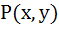 of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is 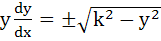
|
IIT 1994 |
|
|
744 |
If f(x) = 3x – 5 then 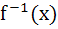 a) is given by 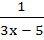 b) is given by 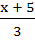 c) does not exist because f is not one-one d) does not exist because f is not onto
If f(x) = 3x – 5 then 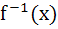 a) is given by 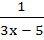 b) is given by 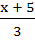 c) does not exist because f is not one-one d) does not exist because f is not onto
|
IIT 1998 |
|
|
745 |
Find the integral solutions of the following system of inequality
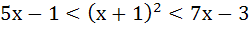 a) x = 1 b) x = 2 c) x = 3 d) x = 4
Find the integral solutions of the following system of inequality
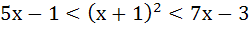 a) x = 1 b) x = 2 c) x = 3 d) x = 4
|
IIT 1979 |
|
|
746 |
Area bounded by 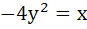 and and 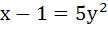
Area bounded by 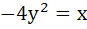 and and 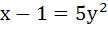
|
IIT 2006 |
|
|
747 |
mn squares of equal size are arranged to form a rectangle of dimension m by n, where m and n are natural numbers. Two squares will be called neighbours if they have exactly one common side. A natural number is written in each square such that the number written in any square is the arithmetic mean of the numbers written in the neighbouring squares. Show that this is possible only if all the numbers used are equal.
mn squares of equal size are arranged to form a rectangle of dimension m by n, where m and n are natural numbers. Two squares will be called neighbours if they have exactly one common side. A natural number is written in each square such that the number written in any square is the arithmetic mean of the numbers written in the neighbouring squares. Show that this is possible only if all the numbers used are equal.
|
IIT 1982 |
|
|
748 |
Let A = 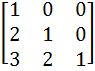
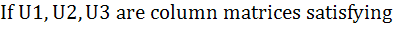
AU1 = 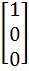 , AU2 = , AU2 = 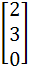 and AU3 = and AU3 = 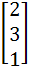
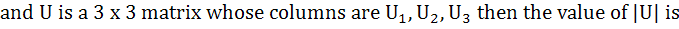 a) 3 b) −3 c)  d) 2
Let A = 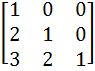
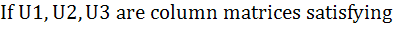
AU1 = 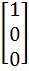 , AU2 = , AU2 = 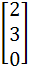 and AU3 = and AU3 = 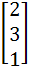
 a) 3 b) −3 c)  d) 2
|
IIT 2006 |
|
|
749 |
The domain of definition of 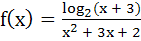 is is a) 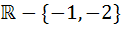 b) 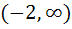 c) 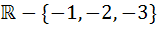 d) 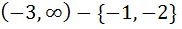
The domain of definition of 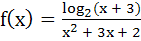 is is a) 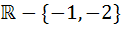 b) 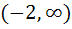 c) 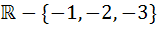 d) 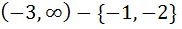
|
IIT 2001 |
|
|
750 |
Let f : ℝ → ℝ be defined by f(x) = 2x + sinx for all x 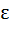 ℝ. Then f is ℝ. Then f is a) One to one and onto b) One to one but not onto c) Onto but not one to one d) Neither one to one nor onto
Let f : ℝ → ℝ be defined by f(x) = 2x + sinx for all x 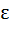 ℝ. Then f is ℝ. Then f is a) One to one and onto b) One to one but not onto c) Onto but not one to one d) Neither one to one nor onto
|
IIT 2002 |
|