|
651 |
If α, β, γ are the cube roots of P, P < 0, then for any x, y, z,
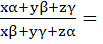 ……….. ………..
If α, β, γ are the cube roots of P, P < 0, then for any x, y, z,
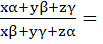 ……….. ………..
|
IIT 1989 |
07:21 min
|
|
652 |
If n is a natural number such that 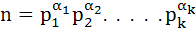 and and 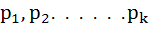 are distinct primes, then show that are distinct primes, then show that
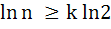
|
IIT 1983 |
03:00 min
|
|
653 |
For any natural number m, show that
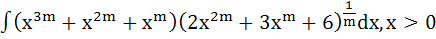 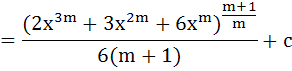
For any natural number m, show that
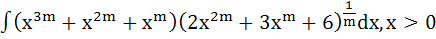 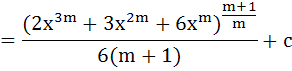
|
IIT 2002 |
04:12 min
|
|
654 |
Let α, β, γ be distinct real numbers. The points with position vectors
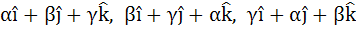 a) Are collinear b) Form an equilateral triangle c) Form a scalene triangle d) Form a right angled triangle
Let α, β, γ be distinct real numbers. The points with position vectors
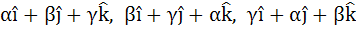 a) Are collinear b) Form an equilateral triangle c) Form a scalene triangle d) Form a right angled triangle
|
IIT 1994 |
03:45 min
|
|
655 |
The least value of the expression 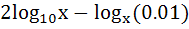 for x > 1 is for x > 1 is a) 10 b) 2 c) −0.01 d) none of these
The least value of the expression 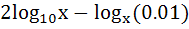 for x > 1 is for x > 1 is a) 10 b) 2 c) −0.01 d) none of these
|
IIT 1980 |
02:59 min
|
|
656 |
The probability that a student passes in Mathematics, Physics and Chemistry are m, p and c respectively. Of these subjects, the student has 75% chances of passing in at least one, a 50% chance of passing in at least two and 40% chance of passing in exactly two. Which of the following relations is true? a) 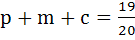 b) 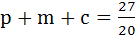 c) 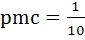 d) 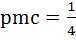
The probability that a student passes in Mathematics, Physics and Chemistry are m, p and c respectively. Of these subjects, the student has 75% chances of passing in at least one, a 50% chance of passing in at least two and 40% chance of passing in exactly two. Which of the following relations is true? a) 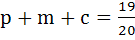 b) 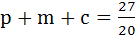 c) 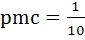 d) 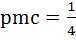
|
IIT 1998 |
08:20 min
|
|
657 |
If 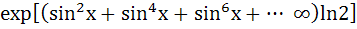 satisfies satisfies 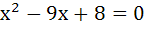 , ,
find the value of 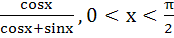
|
IIT 1991 |
04:16 min
|
|
658 |
Let f : ℝ → ℝ and g : ℝ → ℝ be continuous functions. Then the value of integral 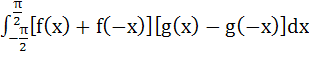 is is a) π b) 1 c) – 1 d) 0
Let f : ℝ → ℝ and g : ℝ → ℝ be continuous functions. Then the value of integral 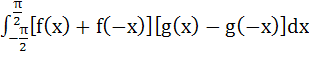 is is a) π b) 1 c) – 1 d) 0
|
IIT 1990 |
01:59 min
|
|
659 |
Let 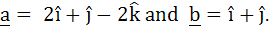 If c is a vector such that If c is a vector such that 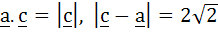 and the angle between and the angle between 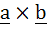 and c is 30° then and c is 30° then 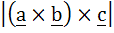 is equal to is equal to a)  b)  c) 2 d) 3
Let 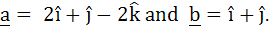 If c is a vector such that If c is a vector such that 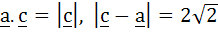 and the angle between and the angle between 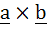 and c is 30° then and c is 30° then 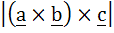 is equal to is equal to a)  b)  c) 2 d) 3
|
IIT 1999 |
03:56 min
|
|
660 |
An anti–aircraft gun can take a maximum of 4 shots at an enemy plane moving away from it. The probability of hitting the plane at the first shot, 2nd, 3rd and 4th shots are 0.4, 0.3, 0.2 and 0.1 respectively. What is the probability that the gun hits the plane?
An anti–aircraft gun can take a maximum of 4 shots at an enemy plane moving away from it. The probability of hitting the plane at the first shot, 2nd, 3rd and 4th shots are 0.4, 0.3, 0.2 and 0.1 respectively. What is the probability that the gun hits the plane?
|
IIT 1981 |
02:45 min
|
|
661 |
The value of the expression 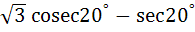 is equal to is equal to a) 2 b) 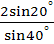 c) 4 d) 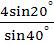
The value of the expression 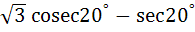 is equal to is equal to a) 2 b) 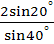 c) 4 d) 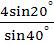
|
IIT 1988 |
02:02 min
|
|
662 |
Let f(x) = 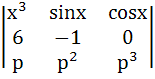 where p is a constant where p is a constant Then 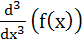 at x = 0 is at x = 0 is a) p b) 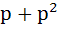 c) 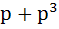 d) Independent of p
Let f(x) = 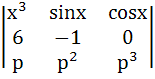 where p is a constant where p is a constant Then 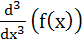 at x = 0 is at x = 0 is a) p b) 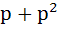 c) 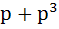 d) Independent of p
|
IIT 1997 |
04:22 min
|
|
663 |
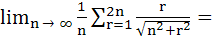
a) 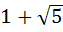 b) 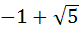 c) 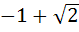 d) 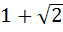
|
IIT 1997 |
02:03 min
|
|
664 |
A and B are independent events. The probability that both A and B occur is  and probability that neither of them occur is and probability that neither of them occur is  . Find the probability of the occurrence of A. . Find the probability of the occurrence of A.
A and B are independent events. The probability that both A and B occur is  and probability that neither of them occur is and probability that neither of them occur is  . Find the probability of the occurrence of A. . Find the probability of the occurrence of A.
|
IIT 1984 |
04:43 min
|
|
665 |
Let 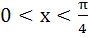 then then 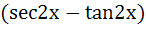 equals equals a) tan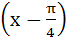 b) tan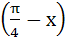 c) tan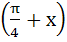 d) tan2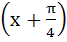
Let 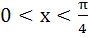 then then 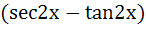 equals equals a) tan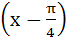 b) tan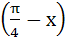 c) tan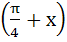 d) tan2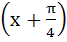
|
IIT 1994 |
02:33 min
|
|
666 |
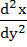 equals equals
a) 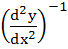 b) 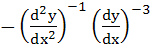 c) 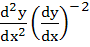 d) 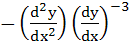
|
IIT 2007 |
01:21 min
|
|
667 |
If f(x) = x – [x] for every real number x, where [x] is the integral part of x, then 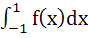 is is a) 1 b) 2 c) 0 d) 
If f(x) = x – [x] for every real number x, where [x] is the integral part of x, then 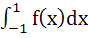 is is a) 1 b) 2 c) 0 d) 
|
IIT 1998 |
02:21 min
|
|
668 |
If a and b are two unit vectors such that 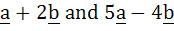 are perpendicular to each other then the angle between a and b is are perpendicular to each other then the angle between a and b is a) 45° b) 60° c) 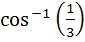 d) 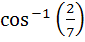
If a and b are two unit vectors such that 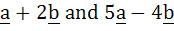 are perpendicular to each other then the angle between a and b is are perpendicular to each other then the angle between a and b is a) 45° b) 60° c) 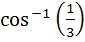 d) 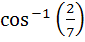
|
IIT 2003 |
01:56 min
|
|
669 |
A man takes a step forward with probability 0.4 and backward with probability 0.6. Find the probability that at the end of eleven steps he is one step away from the starting point.
A man takes a step forward with probability 0.4 and backward with probability 0.6. Find the probability that at the end of eleven steps he is one step away from the starting point.
|
IIT 1987 |
04:29 min
|
|
670 |
The length of longest interval in which the function 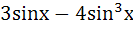 is increasing is is increasing is a)  b)  c) 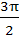 d) 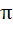
The length of longest interval in which the function 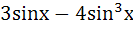 is increasing is is increasing is a)  b)  c) 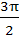 d) 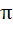
|
IIT 2002 |
01:29 min
|
|
671 |
Let p, q be the roots of the equation 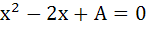 , and r and s are roots of the equation , and r and s are roots of the equation 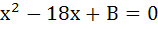 . If . If 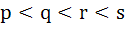 are in arithmetic progression then A = . . . . . , B = . . . . . are in arithmetic progression then A = . . . . . , B = . . . . .
|
IIT 1997 |
03:26 min
|
|
672 |
Let y = 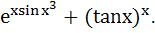 Find Find 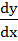 a) 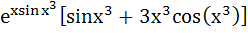 b) 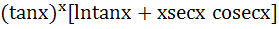 c) 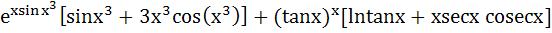 d) 0
Let y = 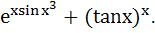 Find Find 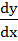 a) 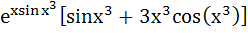 b) 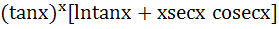 c) 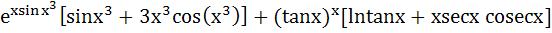 d) 0
|
IIT 1984 |
02:52 min
|
|
673 |
If 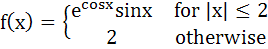 Then 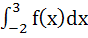 = = a) 0 b) 1 c) 2 d) 3
If 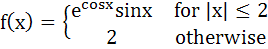 Then 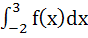 = = a) 0 b) 1 c) 2 d) 3
|
IIT 2000 |
02:01 min
|
|
674 |
If 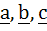 are non-coplanar vectors and are non-coplanar vectors and
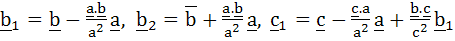 then a.b1 and a. then a.b1 and a.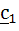 are orthogonal. are orthogonal.
|
IIT 2005 |
02:29 min
|
|
675 |
Let A be a set containing n elements. A subset P of A is constructed at random. The set A is reconstructed by replacing the elements of P. A subset of Q of A is again chosen at random. Find the probability that P and Q have no elements in common.
Let A be a set containing n elements. A subset P of A is constructed at random. The set A is reconstructed by replacing the elements of P. A subset of Q of A is again chosen at random. Find the probability that P and Q have no elements in common.
|
IIT 1990 |
04:10 min
|