|
551 |
For a > 0, d > 0, find the value of the determinant
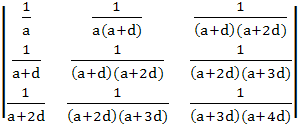 a) 0 b) 1 c) 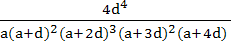 d) 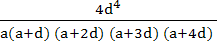
For a > 0, d > 0, find the value of the determinant
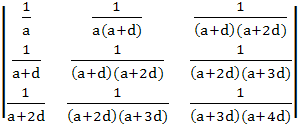 a) 0 b) 1 c) 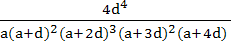 d) 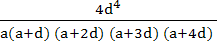
|
IIT 1996 |
05:35 min
|
|
552 |
Multiple choices For real x, the function 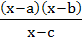 will assume all real values provided will assume all real values provided a) 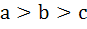 b) 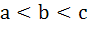 c) 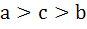 d) 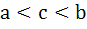
Multiple choices For real x, the function 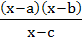 will assume all real values provided will assume all real values provided a) 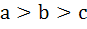 b) 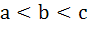 c) 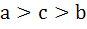 d) 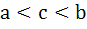
|
IIT 1984 |
05:06 min
|
|
553 |
If the matrix A is equal to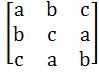 where a, b, c are real positive numbers, abc = 1 and ATA = I then find the value of a3 + b3 + c3. where a, b, c are real positive numbers, abc = 1 and ATA = I then find the value of a3 + b3 + c3. a) 1 b) 2 c) 3 d) 4
If the matrix A is equal to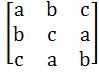 where a, b, c are real positive numbers, abc = 1 and ATA = I then find the value of a3 + b3 + c3. where a, b, c are real positive numbers, abc = 1 and ATA = I then find the value of a3 + b3 + c3. a) 1 b) 2 c) 3 d) 4
|
IIT 2003 |
04:04 min
|
|
554 |
Prove if α, β are roots of the equation 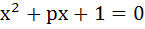 and γ, δ are roots of and γ, δ are roots of 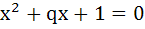 then show that then show that
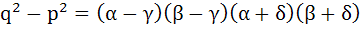
|
IIT 1978 |
03:39 min
|
|
555 |
If the function f: [0, 4] → ℝ is differentiable, then for a, b ε [0, 4] 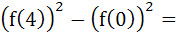 a) 8 f (a) f (b) b) 8 f (a) f '(b) c) 8 f '(a) f (b) d) 8 f '(a) f '(b)
If the function f: [0, 4] → ℝ is differentiable, then for a, b ε [0, 4] 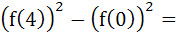 a) 8 f (a) f (b) b) 8 f (a) f '(b) c) 8 f '(a) f (b) d) 8 f '(a) f '(b)
|
IIT 2003 |
01:57 min
|
|
556 |
Find the equation of the common tangent in the first quadrant to the circle 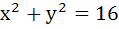 and the ellipse and the ellipse 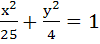 . Also find the length of the intercept of the tangent between the coordinate axis. . Also find the length of the intercept of the tangent between the coordinate axis.
Find the equation of the common tangent in the first quadrant to the circle 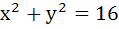 and the ellipse and the ellipse 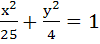 . Also find the length of the intercept of the tangent between the coordinate axis. . Also find the length of the intercept of the tangent between the coordinate axis.
|
IIT 2005 |
06:45 min
|
|
557 |
A determinant is chosen at random from the set of all determinants of order 2 with elements 0 or 1 only. The probability that the value of the determinant chosen is positive is a)  b)  c) 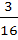 d) 
A determinant is chosen at random from the set of all determinants of order 2 with elements 0 or 1 only. The probability that the value of the determinant chosen is positive is a)  b)  c) 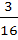 d) 
|
IIT 1982 |
03:18 min
|
|
558 |
If one root of 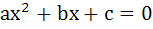 is equal to the is equal to the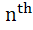 power of the other then show that power of the other then show that
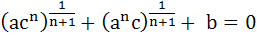
|
IIT 1983 |
02:26 min
|
|
559 |
For 0 < a < x the minimum value of the function logax + logxa is 2. a) True b) False
For 0 < a < x the minimum value of the function logax + logxa is 2. a) True b) False
|
IIT 1984 |
01:26 min
|
|
560 |
The curve described parametrically by 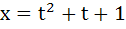 , , 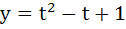 represents represents a) A pair of straight lines b) An ellipse c) A parabola d) A hyperbola
The curve described parametrically by 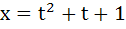 , , 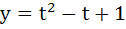 represents represents a) A pair of straight lines b) An ellipse c) A parabola d) A hyperbola
|
IIT 1999 |
01:59 min
|
|
561 |
If a, b, c are in Geometric Progression then the equations 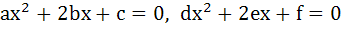
have a common root if 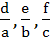 are in are in a) Arithmetic Progression b) Geometric Progression c) Harmonic Progression d) None of these
If a, b, c are in Geometric Progression then the equations 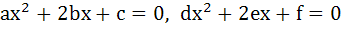
have a common root if 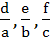 are in are in a) Arithmetic Progression b) Geometric Progression c) Harmonic Progression d) None of these
|
IIT 1985 |
03:08 min
|
|
562 |
The circle 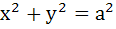 intersects hyperbola intersects hyperbola 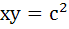 in four points in four points 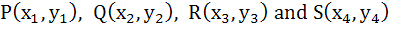 then then a) 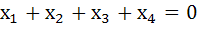 b) 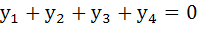 c) 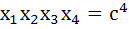 d) 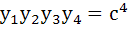
The circle 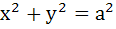 intersects hyperbola intersects hyperbola 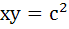 in four points in four points 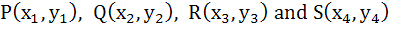 then then a) 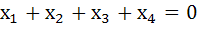 b) 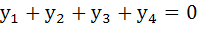 c) 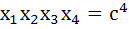 d) 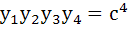
|
IIT 1998 |
02:27 min
|
|
563 |
Solve for x in the following equation 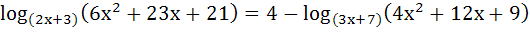
Solve for x in the following equation 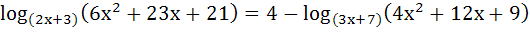
|
IIT 1987 |
07:03 min
|
|
564 |
Let Tr be the rth term of an Arithmetic Progression for 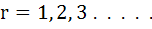 If for some positive integers m, n we have If for some positive integers m, n we have 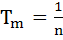 and and 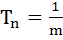 then Tmn equals then Tmn equals a) 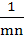 b) 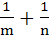 c) 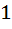 d) 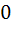
Let Tr be the rth term of an Arithmetic Progression for 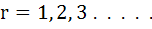 If for some positive integers m, n we have If for some positive integers m, n we have 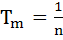 and and 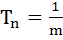 then Tmn equals then Tmn equals a) 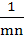 b) 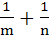 c) 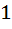 d) 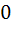
|
IIT 1998 |
01:51 min
|
|
565 |
The probability that at least one of the events A and B occurs is 0.6. If A and B occur simultaneously with probability 0.2 then 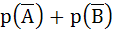 is is a) 0.4 b) 0.8 c) 1.2 d) 1.4
The probability that at least one of the events A and B occurs is 0.6. If A and B occur simultaneously with probability 0.2 then 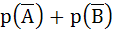 is is a) 0.4 b) 0.8 c) 1.2 d) 1.4
|
IIT 1987 |
02:39 min
|
|
566 |
Consider an infinite geometric series with first term a and common ratio r. If its sum is four and the second term is  then then a) 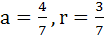 b) 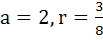 c) 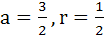 d) 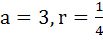
Consider an infinite geometric series with first term a and common ratio r. If its sum is four and the second term is  then then a) 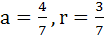 b) 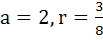 c) 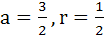 d) 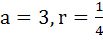
|
IIT 2000 |
01:48 min
|
|
567 |
The probability of India winning a test match against West Indies is ½. Assuming independence of outcomes in each match, the probability that in a 5 test match series India’s second win will occur in the third test is a)  b)  c)  d) 
The probability of India winning a test match against West Indies is ½. Assuming independence of outcomes in each match, the probability that in a 5 test match series India’s second win will occur in the third test is a)  b)  c)  d) 
|
IIT 1995 |
02:40 min
|
|
568 |
For every positive integer n, prove that
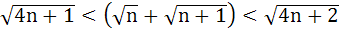
Hence or otherwise prove that
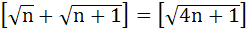
Where [ ] denotes greatest integer not exceeding x.
For every positive integer n, prove that
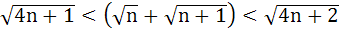
Hence or otherwise prove that
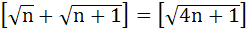
Where [ ] denotes greatest integer not exceeding x.
|
IIT 2000 |
03:07 min
|
|
569 |
If 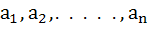 are positive real numbers whose product is a fixed number c then the minimum value of are positive real numbers whose product is a fixed number c then the minimum value of
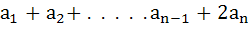 is is a) 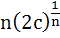 b) 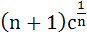 c) 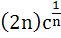 d) 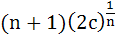
If 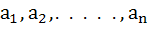 are positive real numbers whose product is a fixed number c then the minimum value of are positive real numbers whose product is a fixed number c then the minimum value of
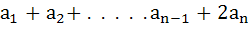 is is a) 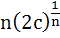 b) 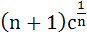 c) 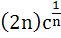 d) 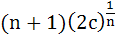
|
IIT 2002 |
01:19 min
|
|
570 |
If from each of the three boxes containing 3 white and one black; 2 white and 2 black; 1 white and 3 black balls, one ball is drawn at random then the probability that 2 white and 1 black ball will be drawn is a) 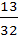 b)  c) 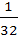 d) 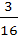
If from each of the three boxes containing 3 white and one black; 2 white and 2 black; 1 white and 3 black balls, one ball is drawn at random then the probability that 2 white and 1 black ball will be drawn is a) 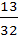 b)  c) 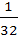 d) 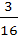
|
IIT 1998 |
02:35 min
|
|
571 |
Let a and b the roots of the equation 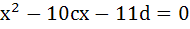 and those of and those of 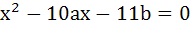 are c and d, then find the value of a + b + c + d when a ≠ b ≠ c ≠ d. are c and d, then find the value of a + b + c + d when a ≠ b ≠ c ≠ d.
Let a and b the roots of the equation 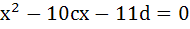 and those of and those of 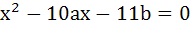 are c and d, then find the value of a + b + c + d when a ≠ b ≠ c ≠ d. are c and d, then find the value of a + b + c + d when a ≠ b ≠ c ≠ d.
|
IIT 2006 |
06:39 min
|
|
572 |
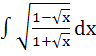 = = 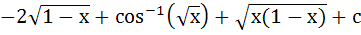
a) True b) False
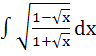 = = 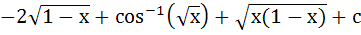
a) True b) False
|
IIT 1985 |
04:05 min
|
|
573 |
The scalar 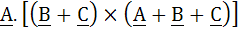 equals equals a) 0 b) 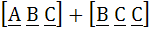 c) 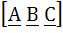 d) None of these
The scalar 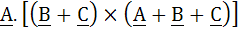 equals equals a) 0 b) 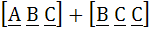 c) 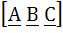 d) None of these
|
IIT 1981 |
02:30 min
|
|
574 |
Fill in the blanks If 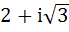 is a root of the equation is a root of the equation 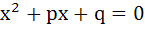 where p and q are real then (p, q) where p and q are real then (p, q)  ………… …………
Fill in the blanks If 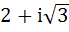 is a root of the equation is a root of the equation 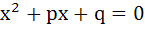 where p and q are real then (p, q) where p and q are real then (p, q)  ………… …………
|
IIT 1982 |
02:44 min
|
|
575 |
If the mth, nth and pth term of an Arithmetic Progression and a Geometric Progression are equal and are x, y, z then prove that
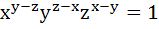
If the mth, nth and pth term of an Arithmetic Progression and a Geometric Progression are equal and are x, y, z then prove that
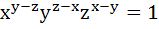
|
IIT 1979 |
06:24 min
|