|
501 |
If 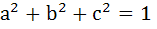 then ab + bc + ca lies in the interval then ab + bc + ca lies in the interval a) 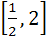 b) 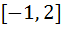 c) 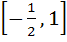 d) 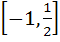
If 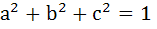 then ab + bc + ca lies in the interval then ab + bc + ca lies in the interval a) 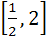 b) 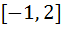 c) 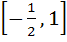 d) 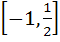
|
IIT 1984 |
02:29 min
|
|
502 |
Find the values of x and y for which the following equation is satisfied 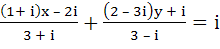 a) x = y = −1 b) x = y = 3 c) x = 1, y = 3 d) x = 3, y = −1
Find the values of x and y for which the following equation is satisfied 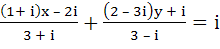 a) x = y = −1 b) x = y = 3 c) x = 1, y = 3 d) x = 3, y = −1
|
IIT 1980 |
05:23 min
|
|
503 |
The equation of the directrix of the parabola y2 + 4y + 4x +2 = 0 is a) x = − 1 b) x = 1 c) 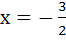 d) 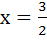
The equation of the directrix of the parabola y2 + 4y + 4x +2 = 0 is a) x = − 1 b) x = 1 c) 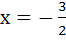 d) 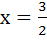
|
IIT 2001 |
01:51 min
|
|
504 |
Let α, β be roots of the equation (x – a) (x – b) = c, c ≠ 0. Then the roots of the equation (x – α) (x – β) + c = 0 are a) a, c b) b, c c) a, b d) a + c, b + c
Let α, β be roots of the equation (x – a) (x – b) = c, c ≠ 0. Then the roots of the equation (x – α) (x – β) + c = 0 are a) a, c b) b, c c) a, b d) a + c, b + c
|
IIT 1992 |
02:15 min
|
|
505 |
If = x + iy then = x + iy then a) x = 3, y = 1 b) x = 1, y = 3 c) x = 0, y = 3 d) x = 0, y = 0
If = x + iy then = x + iy then a) x = 3, y = 1 b) x = 1, y = 3 c) x = 0, y = 3 d) x = 0, y = 0
|
IIT 1998 |
01:25 min
|
|
506 |
It is given that n is an odd integer greater than 3 and not a multiple of 3. Prove that  is a factor of is a factor of 
It is given that n is an odd integer greater than 3 and not a multiple of 3. Prove that  is a factor of is a factor of 
|
IIT 1985 |
07:09 min
|
|
507 |
The focal chord of 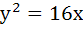 is tangent to is tangent to 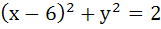 then the possible value of the slope of this chord are then the possible value of the slope of this chord are a) 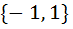 b) 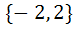 c) 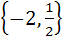 d) 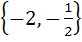
The focal chord of 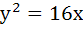 is tangent to is tangent to 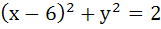 then the possible value of the slope of this chord are then the possible value of the slope of this chord are a) 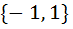 b) 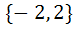 c) 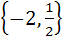 d) 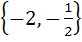
|
IIT 2003 |
02:51 min
|
|
508 |
If p, q ε {1, 2, 3, 4}. The number of equations of the form 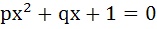 having real roots is having real roots is a) 15 b) 9 c) 7 d) 8
If p, q ε {1, 2, 3, 4}. The number of equations of the form 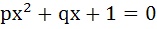 having real roots is having real roots is a) 15 b) 9 c) 7 d) 8
|
IIT 1994 |
03:39 min
|
|
509 |
If A =  and B = and B =  then the value of α for which A2 = B is then the value of α for which A2 = B is a) 1 b) −1 c) 4 d) No real values
If A =  and B = and B =  then the value of α for which A2 = B is then the value of α for which A2 = B is a) 1 b) −1 c) 4 d) No real values
|
IIT 2003 |
01:17 min
|
|
510 |
If 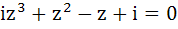 then show that |z| = 1. then show that |z| = 1.
If 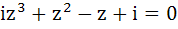 then show that |z| = 1. then show that |z| = 1.
|
IIT 1995 |
02:14 min
|
|
511 |
Suppose that the normals drawn at three different points on the parabola 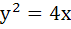 pass through the point (h, 0). Show that h > 2. pass through the point (h, 0). Show that h > 2.
Suppose that the normals drawn at three different points on the parabola 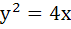 pass through the point (h, 0). Show that h > 2. pass through the point (h, 0). Show that h > 2.
|
IIT 1981 |
03:52 min
|
|
512 |
Through the vertex O of the parabola 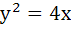 chords OP and OQ are drawn at right angles. Show that for all positions of P, PQ cuts the axis of the parabola at a fixed point. Also find the locus of the midpoint of PQ. chords OP and OQ are drawn at right angles. Show that for all positions of P, PQ cuts the axis of the parabola at a fixed point. Also find the locus of the midpoint of PQ.
Through the vertex O of the parabola 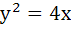 chords OP and OQ are drawn at right angles. Show that for all positions of P, PQ cuts the axis of the parabola at a fixed point. Also find the locus of the midpoint of PQ. chords OP and OQ are drawn at right angles. Show that for all positions of P, PQ cuts the axis of the parabola at a fixed point. Also find the locus of the midpoint of PQ.
|
IIT 1994 |
05:22 min
|
|
513 |
For all x ε ( 0, 1 ) a) 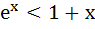 b) ln (1 + x) < x c) sinx > x d) lnx > x
For all x ε ( 0, 1 ) a) 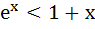 b) ln (1 + x) < x c) sinx > x d) lnx > x
|
IIT 2000 |
02:40 min
|
|
514 |
Given x = cy + bz, y = az + cx, z = bx + ay where x, y, z are not all zero, prove that a2 + b2 + c2 + 2abc = 1
Given x = cy + bz, y = az + cx, z = bx + ay where x, y, z are not all zero, prove that a2 + b2 + c2 + 2abc = 1
|
IIT 1978 |
03:30 min
|
|
515 |
Let  and and 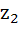 are two complex numbers such that are two complex numbers such that 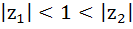 then prove that then prove that 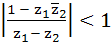 . .
|
IIT 2003 |
04:08 min
|
|
516 |
The number of values of k for which the system of equations (k + 1) x + 8y = 4k kx + ( k + 3 ) y = 3k – 1 has infinitely many solutions is a) 0 b) 1 c) 2 d) Infinity
The number of values of k for which the system of equations (k + 1) x + 8y = 4k kx + ( k + 3 ) y = 3k – 1 has infinitely many solutions is a) 0 b) 1 c) 2 d) Infinity
|
IIT 2002 |
02:56 min
|
|
517 |
If  are positive real numbers whose product is a fixed number c then the minimum value of are positive real numbers whose product is a fixed number c then the minimum value of 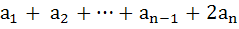 is is a) 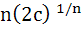 b) 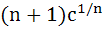 c) 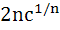 d) 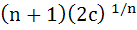
If  are positive real numbers whose product is a fixed number c then the minimum value of are positive real numbers whose product is a fixed number c then the minimum value of 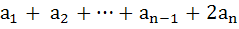 is is a) 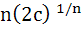 b) 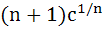 c) 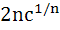 d) 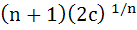
|
IIT 2002 |
02:06 min
|
|
518 |
If three complex numbers are in arithmetic progression then they lie on a circle in the complex plane. a) True b) False
If three complex numbers are in arithmetic progression then they lie on a circle in the complex plane. a) True b) False
|
IIT 1985 |
01:13 min
|
|
519 |
A solution of the differential equation  is is a) y = 2 b) y = 2x c) 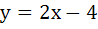 d) 2
A solution of the differential equation  is is a) y = 2 b) y = 2x c) 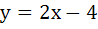 d) 2
|
IIT 1999 |
01:47 min
|
|
520 |
For all x, 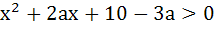 then the interval in which a lies is then the interval in which a lies is a) a < 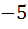 b)  c)  d) 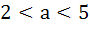
For all x, 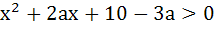 then the interval in which a lies is then the interval in which a lies is a) a < 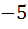 b)  c)  d) 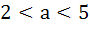
|
IIT 2004 |
01:45 min
|
|
521 |
Let the three digit numbers A28, 3B9 and 62C where A, B, C are integers between 0 and 9, be divisible by a fixed number k. Show that the determinant
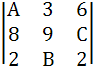 is divisible by k.
Let the three digit numbers A28, 3B9 and 62C where A, B, C are integers between 0 and 9, be divisible by a fixed number k. Show that the determinant
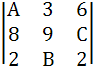 is divisible by k.
|
IIT 1990 |
04:45 min
|
|
522 |
If a and b are real numbers between 0 and 1 such that the points 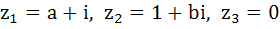 form an equilateral triangle then a is equal to . . . . form an equilateral triangle then a is equal to . . . . a) 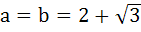 b) 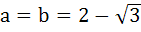 c) 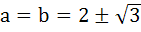 d) 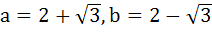
If a and b are real numbers between 0 and 1 such that the points 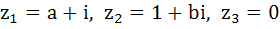 form an equilateral triangle then a is equal to . . . . form an equilateral triangle then a is equal to . . . . a) 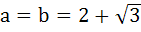 b) 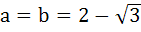 c) 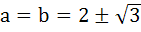 d) 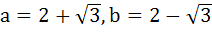
|
IIT 1989 |
03:07 min
|
|
523 |
Let E be the ellipse 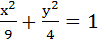 and C be the circle and C be the circle 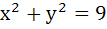 . Let P and Q be the points (1, 2) and (2, 1) respectively. Then . Let P and Q be the points (1, 2) and (2, 1) respectively. Then a) Q lies inside C but outside E b) Q lies outside both C and E c) P lies inside both C and E d) P lies inside C but outside E
Let E be the ellipse 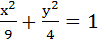 and C be the circle and C be the circle 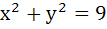 . Let P and Q be the points (1, 2) and (2, 1) respectively. Then . Let P and Q be the points (1, 2) and (2, 1) respectively. Then a) Q lies inside C but outside E b) Q lies outside both C and E c) P lies inside both C and E d) P lies inside C but outside E
|
IIT 1994 |
04:15 min
|
|
524 |
Let a, b, c be the sides of a triangle where a ≠ c and λ ε R. If roots of the equation 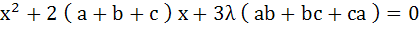 are real then are real then a) 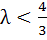 b) 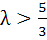 c) 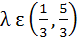 d) 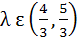
Let a, b, c be the sides of a triangle where a ≠ c and λ ε R. If roots of the equation 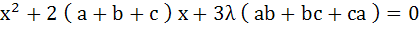 are real then are real then a) 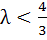 b) 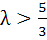 c) 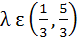 d) 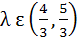
|
IIT 2006 |
04:47 min
|
|
525 |
Find the value of the determinant
 where a, b, c are respectively pth, qth and rth term of a harmonic progression. a) 0 b) 1 c) ½ d) None of the above
Find the value of the determinant
 where a, b, c are respectively pth, qth and rth term of a harmonic progression. a) 0 b) 1 c) ½ d) None of the above
|
IIT 1997 |
04:23 min
|