|
476 |
Which of the following are rational? a) 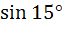 b) 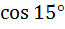 c) 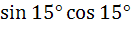 d) 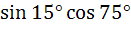
Which of the following are rational? a) 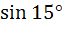 b) 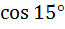 c) 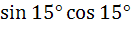 d) 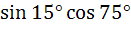
|
IIT 1998 |
02:53 min
|
|
477 |
Using mathematical induction prove that
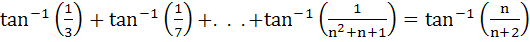
Using mathematical induction prove that
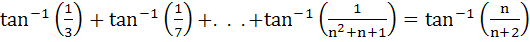
|
IIT 1993 |
08:39 min
|
|
478 |
For x ε R, 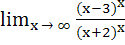 is equal to is equal to a) e b) 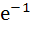 c) 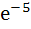 d) 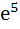
For x ε R, 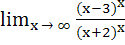 is equal to is equal to a) e b) 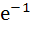 c) 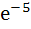 d) 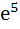
|
IIT 2000 |
06:08 min
|
|
479 |
Find the centre of the circle passing through (0, 0) and (1, 0) and touching the circle 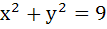 . .
Find the centre of the circle passing through (0, 0) and (1, 0) and touching the circle 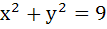 . .
|
IIT 1992 |
06:33 min
|
|
480 |
The number of integral values of k for which the equation 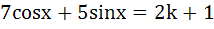 has a solution is has a solution is a) 4 b) 8 c) 10 d) 12
The number of integral values of k for which the equation 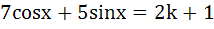 has a solution is has a solution is a) 4 b) 8 c) 10 d) 12
|
IIT 2002 |
03:40 min
|
|
481 |
Evaluate if sin |x| - |x| is differentiable at x = 0. a) Yes b) No
Evaluate if sin |x| - |x| is differentiable at x = 0. a) Yes b) No
|
IIT 2001 |
04:00 min
|
|
482 |
Prove that 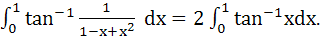 Hence or otherwise evaluate the integral Hence or otherwise evaluate the integral 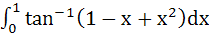 . .
Prove that 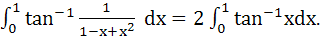 Hence or otherwise evaluate the integral Hence or otherwise evaluate the integral 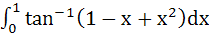 . .
|
IIT 1998 |
05:19 min
|
|
483 |
Fill in the blank Let A, B, C be three vectors of length 3, 4, 5 respectively. Let A is perpendicular to B + C, B is perpendicular to C + A, and C is perpendicular to A + B then the length of the vector 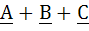 is equal to . . . . is equal to . . . .
Fill in the blank Let A, B, C be three vectors of length 3, 4, 5 respectively. Let A is perpendicular to B + C, B is perpendicular to C + A, and C is perpendicular to A + B then the length of the vector 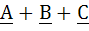 is equal to . . . . is equal to . . . .
|
IIT 1981 |
02:17 min
|
|
484 |
The number of common tangents to the circles 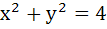 and and 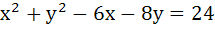 is is a) 0 b) 1 c) 3 d) 4
The number of common tangents to the circles 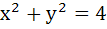 and and 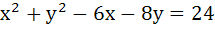 is is a) 0 b) 1 c) 3 d) 4
|
IIT 1998 |
04:08 min
|
|
485 |
Use mathematical induction to show that (25)n + 1 – 24n + 5735 is divisible by (24)2 for all n = 1, 2, . . .
Use mathematical induction to show that (25)n + 1 – 24n + 5735 is divisible by (24)2 for all n = 1, 2, . . .
|
IIT 2002 |
10:18 min
|
|
486 |
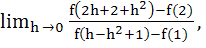 given that given that 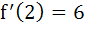 and and 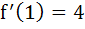
a) does not exist b) is equal to 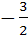 c) is equal to  d) is equal to 3
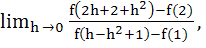 given that given that 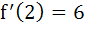 and and 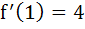
a) does not exist b) is equal to 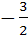 c) is equal to  d) is equal to 3
|
IIT 2003 |
02:46 min
|
|
487 |
If 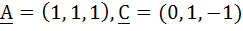 are given vectors then the vector B satisfying the equation are given vectors then the vector B satisfying the equation 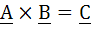 and and 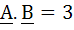 is . . . . . is . . . . .
|
IIT 1985 |
03:28 min
|
|
488 |
If the circles 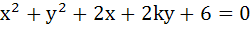 and and 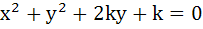 intersect orthogonally then k is intersect orthogonally then k is a) 2 or 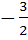 b) – 2 or 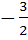 c) 2 or  d) – 2 or 
If the circles 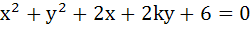 and and 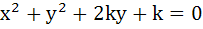 intersect orthogonally then k is intersect orthogonally then k is a) 2 or 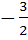 b) – 2 or 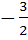 c) 2 or  d) – 2 or 
|
IIT 2000 |
02:40 min
|
|
489 |
In a ΔABC, 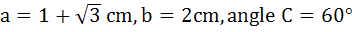 then find the other sides and angles then find the other sides and angles a) A = 60°, B = 60°, c = 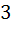 b) A = 45°, B = 75°, c = 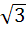 c) A = 75°, B = 45°, c = 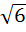 d) A = 15°, B = 105°, c = 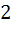
In a ΔABC, 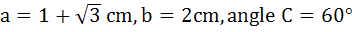 then find the other sides and angles then find the other sides and angles a) A = 60°, B = 60°, c = 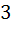 b) A = 45°, B = 75°, c = 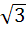 c) A = 75°, B = 45°, c = 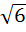 d) A = 15°, B = 105°, c = 
|
IIT 1978 |
03:06 min
|
|
490 |
(1 + ax)n = 1 + 8x + 24x2 + . . . then a = . . ., n = . . .
(1 + ax)n = 1 + 8x + 24x2 + . . . then a = . . ., n = . . .
|
IIT 1983 |
02:24 min
|
|
491 |
Given that a = (1, 1, 1), c = (0, 1, −1), a . b = 3, 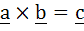 then b is equal to then b is equal to
Given that a = (1, 1, 1), c = (0, 1, −1), a . b = 3, 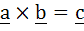 then b is equal to then b is equal to
|
IIT 1991 |
02:22 min
|
|
492 |
If a > 2b > 0 then the positive value of m for which
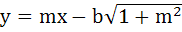 is a common tangent to is a common tangent to 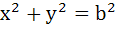 and and 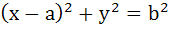 is is a) 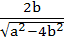 b) 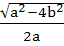 c) 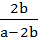 d) 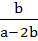
If a > 2b > 0 then the positive value of m for which
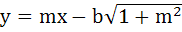 is a common tangent to is a common tangent to 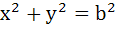 and and 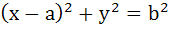 is is a) 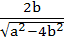 b) 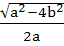 c) 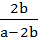 d) 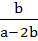
|
IIT 2002 |
05:23 min
|
|
493 |
Find the coordinates of the point of intersection of the curves
y = cosx and y = sin3x if 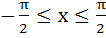 . . a) (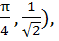 ( (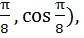 ( (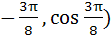 b) (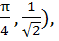 ( (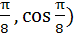 c) (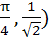 d) (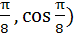
|
IIT 1982 |
03:54 min
|
|
494 |
If f (x) = cos (lnx) then f (x) f (y) −  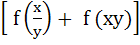 has the value of has the value of a) −1 b)  c) −2 d) None of these
If f (x) = cos (lnx) then f (x) f (y) −  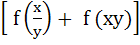 has the value of has the value of a) −1 b)  c) −2 d) None of these
|
IIT 1983 |
02:43 min
|
|
495 |
Multiple choices The function 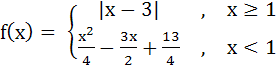 a) continuous at x = 1 b) differentiable at x = 1 c) continuous at x = 3 d) differentiable at x = 3
Multiple choices The function 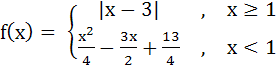 a) continuous at x = 1 b) differentiable at x = 1 c) continuous at x = 3 d) differentiable at x = 3
|
IIT 1988 |
04:52 min
|
|
496 |
The value of 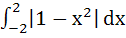 is is a) 0 b) 1 c) 2 d) 4
The value of 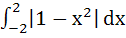 is is a) 0 b) 1 c) 2 d) 4
|
IIT 1989 |
03:14 min
|
|
497 |
If b and c are any two non-collinear unit vectors and a is any vector then 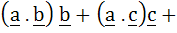 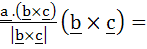 . . . . . . . . . .
If b and c are any two non-collinear unit vectors and a is any vector then 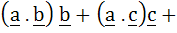 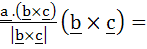 . . . . . . . . . .
|
IIT 1996 |
03:25 min
|
|
498 |
Tangent to the curve 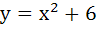 at the point P(1, 7) touches the circle at the point P(1, 7) touches the circle 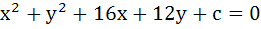 at a point Q then the coordinates of Q are at a point Q then the coordinates of Q are a) 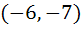 b) 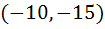 c) 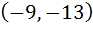 d) 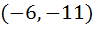
Tangent to the curve 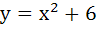 at the point P(1, 7) touches the circle at the point P(1, 7) touches the circle 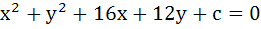 at a point Q then the coordinates of Q are at a point Q then the coordinates of Q are a) 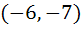 b) 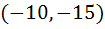 c) 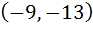 d) 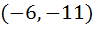
|
IIT 2005 |
05:15 min
|
|
499 |
For n > 0, 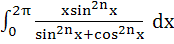 is is a)  b) π c) 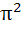 d) 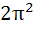
For n > 0, 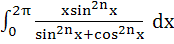 is is a)  b) π c) 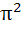 d) 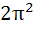
|
IIT 1996 |
08:23 min
|
|
500 |
The value of the definite integral 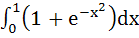 is is a) – 1 b) 2 c) 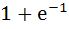 d) 
The value of the definite integral 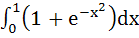 is is a) – 1 b) 2 c) 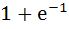 d) 
|
IIT 1981 |
02:44 min
|