|
451 |
Evaluate 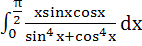 a) 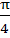 b) 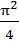 c) 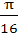 d) 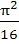
|
IIT 1985 |
04:33 min
|
|
452 |
Let C be the curve 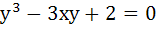 . If H is the set of points on the curve C when the tangent is horizontal and v be the set of all points on the curve C when the tangent is vertical then H = . . . . . and v = . . . . . . If H is the set of points on the curve C when the tangent is horizontal and v be the set of all points on the curve C when the tangent is vertical then H = . . . . . and v = . . . . .
Let C be the curve 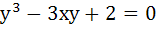 . If H is the set of points on the curve C when the tangent is horizontal and v be the set of all points on the curve C when the tangent is vertical then H = . . . . . and v = . . . . . . If H is the set of points on the curve C when the tangent is horizontal and v be the set of all points on the curve C when the tangent is vertical then H = . . . . . and v = . . . . .
|
IIT 1994 |
04:09 min
|
|
453 |
In a triangle ABC, angle A is greater than angle B. If the measures of angle A and B satisfy the equation 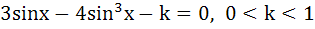 , then the measure of angle C is , then the measure of angle C is a)  b)  c) 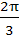 d) 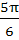
In a triangle ABC, angle A is greater than angle B. If the measures of angle A and B satisfy the equation 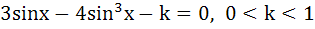 , then the measure of angle C is , then the measure of angle C is a)  b)  c) 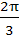 d) 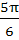
|
IIT 1990 |
01:43 min
|
|
454 |
Prove that C0 – 22C1 + 32C2 − . . . + (−)n (n + 1)2 Cn = 0 for n > 2 where 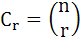
Prove that C0 – 22C1 + 32C2 − . . . + (−)n (n + 1)2 Cn = 0 for n > 2 where 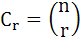
|
IIT 1989 |
05:31 min
|
|
455 |
Show that 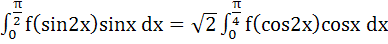
Show that 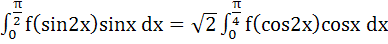
|
IIT 1990 |
05:42 min
|
|
456 |
The centre of the circle passing through (0, 1) and touching the curve 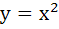 at (2, 4) is at (2, 4) is a) 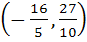 b) 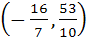 c) 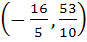 d) None of these
The centre of the circle passing through (0, 1) and touching the curve 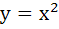 at (2, 4) is at (2, 4) is a) 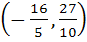 b) 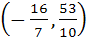 c) 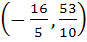 d) None of these
|
IIT 1983 |
07:23 min
|
|
457 |
Determine a positive integer n ≤ 5 such that 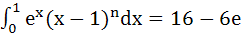 . . a) 1 b) 2 c) 3 d) 4
Determine a positive integer n ≤ 5 such that 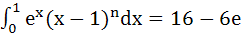 . . a) 1 b) 2 c) 3 d) 4
|
IIT 1992 |
04:02 min
|
|
458 |
If a, b, c, d are distinct vectors satisfying relation 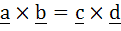 and and 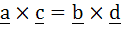 . Prove that . Prove that 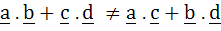
|
IIT 2004 |
02:40 min
|
|
459 |
If two circles 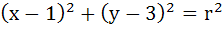 and and 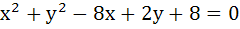 intersect in two distinct points, then intersect in two distinct points, then a) 2 < r < 8 b) r < 2 c) r = 2 d) r > 2
If two circles 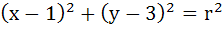 and and 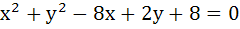 intersect in two distinct points, then intersect in two distinct points, then a) 2 < r < 8 b) r < 2 c) r = 2 d) r > 2
|
IIT 1989 |
04:34 min
|
|
460 |
The maximum value of cos 1 cos 1 cos 2 cos 2 cos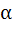 3 …… cos 3 …… cos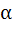 nunder the restriction 0 nunder the restriction 0 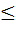 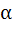 1 , 1 , 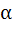 2 , 2 , 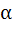 3 …. , 3 …. , 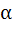 n n 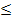 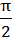 and cot and cot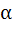 1 cot 1 cot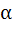 2 cot3 …… cot 2 cot3 …… cot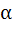 n= 1 is n= 1 is a) 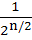 b) 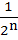 c) 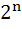 d) 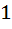
|
IIT 2001 |
03:43 min
|
|
461 |
The left hand derivative of f (x) = [x] sinπx at k, k an integer is a) 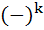 (k – 1)π (k – 1)π b) 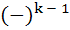 (k – 1)π (k – 1)π c) 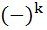 kπ kπ d) 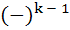 kπ kπ
The left hand derivative of f (x) = [x] sinπx at k, k an integer is a) 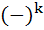 (k – 1)π (k – 1)π b) 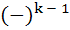 (k – 1)π (k – 1)π c) 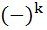 kπ kπ d) 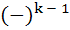 kπ kπ
|
IIT 2001 |
03:56 min
|
|
462 |
Determine the value of 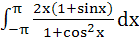 a) 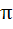 b) 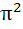 c)  d) 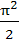
Determine the value of 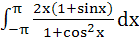 a) 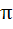 b) 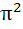 c)  d) 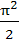
|
IIT 1997 |
06:07 min
|
|
463 |
Let f : ℝ → ℝ be such that f (1) = 3 and 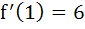 then then 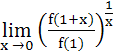 equals equals
a) 1 b) 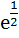 c) 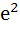 d) 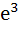
Let f : ℝ → ℝ be such that f (1) = 3 and 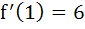 then then 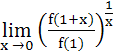 equals equals
a) 1 b) 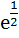 c) 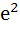 d) 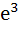
|
IIT 2002 |
02:57 min
|
|
464 |
For x > 0, let 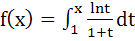 find the function find the function 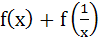 and show that and show that 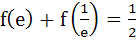 . Here . Here 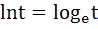 . . a)  b) 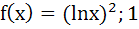 c) 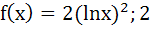 d) 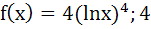
|
IIT 2000 |
06:08 min
|
|
465 |
If two distinct chords drawn from the point (p, q) on the circle 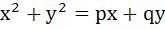 (where pq ≠ 0) are bisected by the X-axis then (where pq ≠ 0) are bisected by the X-axis then a) 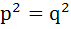 b) 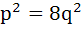 c) 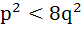 d) 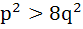
If two distinct chords drawn from the point (p, q) on the circle 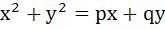 (where pq ≠ 0) are bisected by the X-axis then (where pq ≠ 0) are bisected by the X-axis then a) 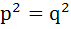 b) 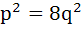 c) 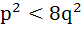 d) 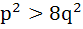
|
IIT 1999 |
05:52 min
|
|
466 |
Let 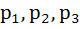 are the perpendiculars from the vertices of a triangle to the opposite sides, then are the perpendiculars from the vertices of a triangle to the opposite sides, then 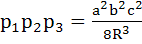 a) True b) False
Let 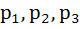 are the perpendiculars from the vertices of a triangle to the opposite sides, then are the perpendiculars from the vertices of a triangle to the opposite sides, then 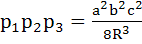 a) True b) False
|
IIT 1978 |
02:41 min
|
|
467 |
The coefficient of x99 in the polynomial
(x – 1) (x – 2) . . . (x – 100) is
The coefficient of x99 in the polynomial
(x – 1) (x – 2) . . . (x – 100) is
|
IIT 1982 |
02:12 min
|
|
468 |
Evaluate 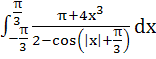
Evaluate 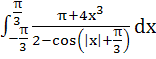
|
IIT 2004 |
07:21 min
|
|
469 |
The sum of the rational terms in the expansion of 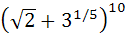 is is
The sum of the rational terms in the expansion of 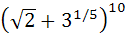 is is
|
IIT 1997 |
03:13 min
|
|
470 |
A unit vector perpendicular to the plane determined by the points P (1, -1, 2), Q (2, 0, -1) and R (0, 2, 1) is . . . . .
A unit vector perpendicular to the plane determined by the points P (1, -1, 2), Q (2, 0, -1) and R (0, 2, 1) is . . . . .
|
IIT 1994 |
03:33 min
|
|
471 |
If one of the diameters of the circle 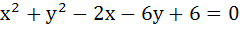 is a chord to the circle with centre (2, 1) then the radius of the circle is is a chord to the circle with centre (2, 1) then the radius of the circle is a) 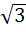 b) 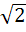 c) 3 d) 2
If one of the diameters of the circle 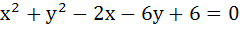 is a chord to the circle with centre (2, 1) then the radius of the circle is is a chord to the circle with centre (2, 1) then the radius of the circle is a) 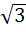 b) 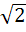 c) 3 d) 2
|
IIT 2004 |
02:47 min
|
|
472 |
Which of the following functions is periodic? a) f(x) = x – [x] where [x] denotes the greatest integer less than or equal to the real number x b) f(x) = sin 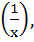 x ≠ 0, f(0) = 0 x ≠ 0, f(0) = 0 c) f(x) = x cos x d) None of these
Which of the following functions is periodic? a) f(x) = x – [x] where [x] denotes the greatest integer less than or equal to the real number x b) f(x) = sin 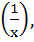 x ≠ 0, f(0) = 0 x ≠ 0, f(0) = 0 c) f(x) = x cos x d) None of these
|
IIT 1983 |
01:19 min
|
|
473 |
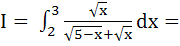
a)  b)  c) 1 d) 2
|
IIT 1994 |
01:46 min
|
|
474 |
Let a, b and c be three vectors having magnitudes 1, 1 and 2 respectively. If 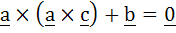 then the acute angle between a and c is . . . . . then the acute angle between a and c is . . . . .
Let a, b and c be three vectors having magnitudes 1, 1 and 2 respectively. If 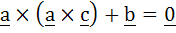 then the acute angle between a and c is . . . . . then the acute angle between a and c is . . . . .
|
IIT 1997 |
04:42 min
|
|
475 |
The equation of the tangents drawn from the origin to the circle 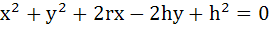 are are a) x= 6 b) y = 0 c) 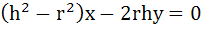 d) 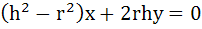
The equation of the tangents drawn from the origin to the circle 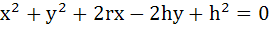 are are a) x= 6 b) y = 0 c) 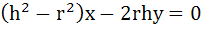 d) 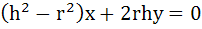
|
IIT 1988 |
04:06 min
|