|
426 |
Let a given line L1 intersect the X-axis and Y-axis at P and Q respectively. Let another line L2 perpendicular to L1 cut the X and Y axis at R and S respectively. Show that the locus of the point of intersection of the lines PS and QR is a circle passing through the origin.
Let a given line L1 intersect the X-axis and Y-axis at P and Q respectively. Let another line L2 perpendicular to L1 cut the X and Y axis at R and S respectively. Show that the locus of the point of intersection of the lines PS and QR is a circle passing through the origin.
|
IIT 1987 |
07:55 min
|
|
427 |
Fill in the blank
General values of θ satisfying the equation 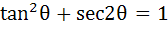 are are a) θ = nπ b) 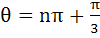 c) 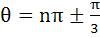 d) θ = nπ or θ = 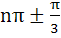
Fill in the blank
General values of θ satisfying the equation 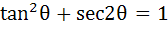 are are a) θ = nπ b) 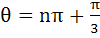 c) 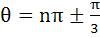 d) θ = nπ or θ = 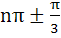
|
IIT 1996 |
02:28 min
|
|
428 |
If f (x + y) = f (x) + f (y) for all x and y. If the function f is continuous at x = 0 then f is continuous for all x. a) True b) False
If f (x + y) = f (x) + f (y) for all x and y. If the function f is continuous at x = 0 then f is continuous for all x. a) True b) False
|
IIT 1981 |
05:14 min
|
|
429 |
How many different 9 digit numbers can be formed from the numbers 223355888 by rearranging its digits so that the odd digits occupy even positions a) 16 b) 36 c) 60 d) 180
How many different 9 digit numbers can be formed from the numbers 223355888 by rearranging its digits so that the odd digits occupy even positions a) 16 b) 36 c) 60 d) 180
|
IIT 2000 |
03:12 min
|
|
430 |
The function defined by 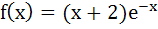 is is a) Decreasing for all x b) Decreasing in 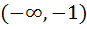 and increasing in and increasing in 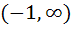 c) Increasing for all x d) Decreasing in 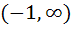 and increasing in and increasing in 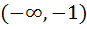
The function defined by 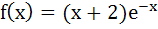 is is a) Decreasing for all x b) Decreasing in 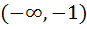 and increasing in and increasing in 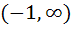 c) Increasing for all x d) Decreasing in 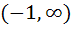 and increasing in and increasing in 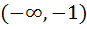
|
IIT 1994 |
01:20 min
|
|
431 |
The principal value of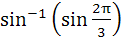 is is a) 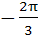 b) 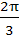 c) 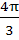 d) 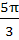 e) None of these
The principal value of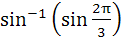 is is a) 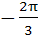 b) 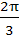 c) 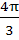 d) 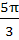 e) None of these
|
IIT 1986 |
01:00 min
|
|
432 |
Let f(x) = 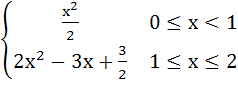 Discuss the continuity of 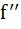 on [0, 2] on [0, 2] a) 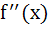 is continuous for all x is continuous for all x 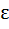 ℝ ℝ b) 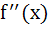 is continuous for all x is continuous for all x 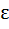 ℝ except at x = 1 ℝ except at x = 1 c) 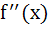 is continuous for all x is continuous for all x 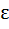 ℝ except at x = 1 and x = 2 ℝ except at x = 1 and x = 2 d) 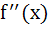 is continuous for all x is continuous for all x 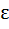 ℝ except at x = 0, x = 1 and x = 2 ℝ except at x = 0, x = 1 and x = 2
|
IIT 1983 |
04:54 min
|
|
433 |
Let a circle be given by 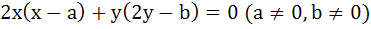 . Find the condition on a and b if two chords each bisected by the X–axis can be drawn from . Find the condition on a and b if two chords each bisected by the X–axis can be drawn from 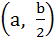 . .
Let a circle be given by 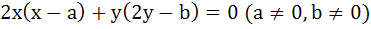 . Find the condition on a and b if two chords each bisected by the X–axis can be drawn from . Find the condition on a and b if two chords each bisected by the X–axis can be drawn from 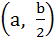 . .
|
IIT 1992 |
06:10 min
|
|
434 |
The value of x for which 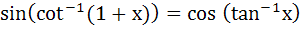 is is a)  b) 1 c) 0 d) 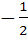
The value of x for which 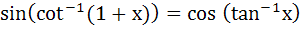 is is a)  b) 1 c) 0 d) 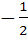
|
IIT 2004 |
02:13 min
|
|
435 |
Consider the following Statement (S) and Reason (R) S: Both sinx, cosx are decreasing functions in the interval 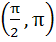 R: If a differentiable function decreases in an interval (a, b) then the derivative also decreases in (a, b) Which of the following is true? a) Both S and R are wrong b) Both S and R are correct but R is not the correct explanation of S c) S is correct and R is the correct explanation of S d) S is correct and R is wrong
Consider the following Statement (S) and Reason (R) S: Both sinx, cosx are decreasing functions in the interval 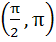 R: If a differentiable function decreases in an interval (a, b) then the derivative also decreases in (a, b) Which of the following is true? a) Both S and R are wrong b) Both S and R are correct but R is not the correct explanation of S c) S is correct and R is the correct explanation of S d) S is correct and R is wrong
|
IIT 2000 |
02:40 min
|
|
436 |
The numerical value of 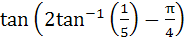 is is a)  b) 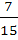 c) 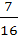 d) 
The numerical value of 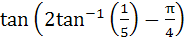 is is a)  b) 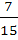 c) 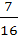 d) 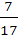
|
IIT 1984 |
02:39 min
|
|
437 |
The range of the function f (x) = 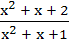 , x ε R is , x ε R is a) ( 1, 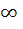 ) ) b) 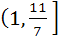 c) 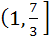 d) 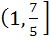
The range of the function f (x) = 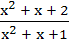 , x ε R is , x ε R is a) ( 1,  ) ) b) 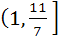 c) 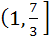 d) 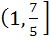
|
IIT 2003 |
02:22 min
|
|
438 |
A function f : ℝ → ℝ satisfies the equation f(x + y) = f(x) . f(y) 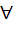 x, y in ℝ and f(x) ≠ 0 for any x in ℝ. Let the function be differentiable at x = 0 and x, y in ℝ and f(x) ≠ 0 for any x in ℝ. Let the function be differentiable at x = 0 and 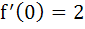 . Show that . Show that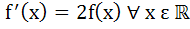 . Hence determine f(x). . Hence determine f(x). a) ex b) e2x c) 2ex d) 2e2x
A function f : ℝ → ℝ satisfies the equation f(x + y) = f(x) . f(y) 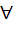 x, y in ℝ and f(x) ≠ 0 for any x in ℝ. Let the function be differentiable at x = 0 and x, y in ℝ and f(x) ≠ 0 for any x in ℝ. Let the function be differentiable at x = 0 and 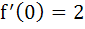 . Show that . Show that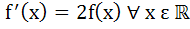 . Hence determine f(x). . Hence determine f(x). a) ex b) e2x c) 2ex d) 2e2x
|
IIT 1990 |
05:07 min
|
|
439 |
m men and n women are to be seated in a row so that no two women sit together. If m > n, then find the number of ways in which they can be seated.
m men and n women are to be seated in a row so that no two women sit together. If m > n, then find the number of ways in which they can be seated.
|
IIT 1983 |
03:36 min
|
|
440 |
In a triangle ABC, 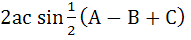 is equal to is equal to a) 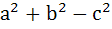 b) 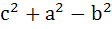 c) 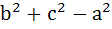 d) 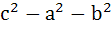
In a triangle ABC, 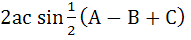 is equal to is equal to a) 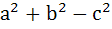 b) 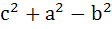 c) 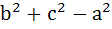 d) 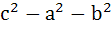
|
IIT 2000 |
01:22 min
|
|
441 |
If F (x) = 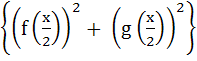 where 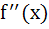 = = 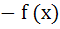 and and 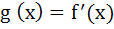 and given that F (5) = 5 and given that F (5) = 5
then F (10) is equal to a) 5 b) 10 c) 0 d) 15
If F (x) = 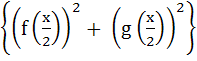 where 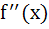 = = 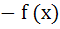 and and 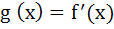 and given that F (5) = 5 and given that F (5) = 5
then F (10) is equal to a) 5 b) 10 c) 0 d) 15
|
IIT 2006 |
02:52 min
|
|
442 |
Eighteen guests have to be seated, half on each side of a long table. Four particular guests desire to be on a particular side and three others on the other side. Determine the number of ways in which the seating arrangements can be made?
Eighteen guests have to be seated, half on each side of a long table. Four particular guests desire to be on a particular side and three others on the other side. Determine the number of ways in which the seating arrangements can be made?
|
IIT 1991 |
03:05 min
|
|
443 |
Tangent is drawn to the ellipse 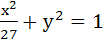 at at  where where 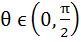 . Then the value of θ such that the sum of intercept on the axes made by the tangents is minimum is . Then the value of θ such that the sum of intercept on the axes made by the tangents is minimum is a)  b)  c)  d) 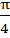
Tangent is drawn to the ellipse 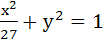 at at  where where 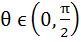 . Then the value of θ such that the sum of intercept on the axes made by the tangents is minimum is . Then the value of θ such that the sum of intercept on the axes made by the tangents is minimum is a)  b)  c)  d) 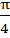
|
IIT 2003 |
07:37 min
|
|
444 |
Let C1 , C2 be two circles with C2 lying inside C1. A circle C lying inside C1 touches C1 internally and C2 externally. Identify the locus of the center of C .
Let C1 , C2 be two circles with C2 lying inside C1. A circle C lying inside C1 touches C1 internally and C2 externally. Identify the locus of the center of C .
|
IIT 2001 |
06:14 min
|
|
445 |
The sides of a triangle are in the ratio 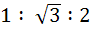 then the angles of the triangle are in the ratio then the angles of the triangle are in the ratio a) 1 : 3 : 5 b) 2 : 3 : 4 c) 3 : 2 : 1 d) 1 : 2 : 3
The sides of a triangle are in the ratio 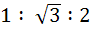 then the angles of the triangle are in the ratio then the angles of the triangle are in the ratio a) 1 : 3 : 5 b) 2 : 3 : 4 c) 3 : 2 : 1 d) 1 : 2 : 3
|
IIT 2004 |
02:52 min
|
|
446 |
Subjective problem Let y = 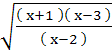 Find all real values of x for which y takes real values a) for x ≥ 3, y is real b) for 2 < x < 3, y is imaginary c) for – 1 ≤ x < 2, y is real d) for x < – 1, y is imaginary
Subjective problem Let y = 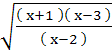 Find all real values of x for which y takes real values a) for x ≥ 3, y is real b) for 2 < x < 3, y is imaginary c) for – 1 ≤ x < 2, y is real d) for x < – 1, y is imaginary
|
IIT 1990 |
03:41 min
|
|
447 |
If f(x) is differentiable and strictly increasing function then the value of 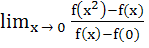 is is a) 1 b) 0 c) – 1 d) 2
If f(x) is differentiable and strictly increasing function then the value of 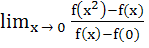 is is a) 1 b) 0 c) – 1 d) 2
|
IIT 2004 |
03:20 min
|
|
448 |
Let R be the set of real numbers and f : R 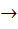 R such that for all x, y ε R, |f (x) – f (y)| ≤ | x – y |2. Then R such that for all x, y ε R, |f (x) – f (y)| ≤ | x – y |2. Then a) 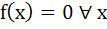 b) f (x) is a constant c) none of the above
Let R be the set of real numbers and f : R  R such that for all x, y ε R, |f (x) – f (y)| ≤ | x – y |2. Then R such that for all x, y ε R, |f (x) – f (y)| ≤ | x – y |2. Then a) 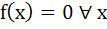 b) f (x) is a constant c) none of the above
|
IIT 1988 |
02:07 min
|
|
449 |
If 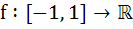 and and 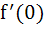 = =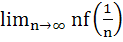 and f(0) = 0. Find the value of and f(0) = 0. Find the value of 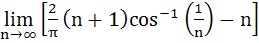 . Given that 0 < . Given that 0 < 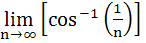 < <  a) 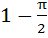 b) 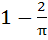 c) 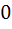 d) 1
|
IIT 2004 |
03:29 min
|
|
450 |
The area bounded by the curves y = (x + 1)2 y = (x – 1)2 and the line 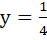 is is a)  b)  c)  d) 
The area bounded by the curves y = (x + 1)2 y = (x – 1)2 and the line 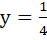 is is a)  b)  c)  d) 
|
IIT 2005 |
06:30 min
|