|
351 |
If 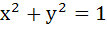 then then a) 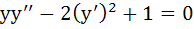 b) 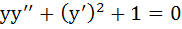 c) 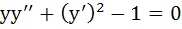 d) 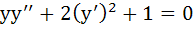
|
IIT 2003 |
00:43 min
|
|
352 |
Let P = (x, y) be any point on 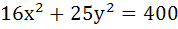 with focii with focii 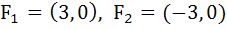 and and 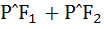 equals equals a) 8 b) 6 c) 10 d) 12
Let P = (x, y) be any point on 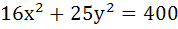 with focii with focii 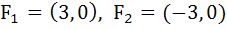 and and 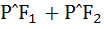 equals equals a) 8 b) 6 c) 10 d) 12
|
IIT 1998 |
01:38 min
|
|
353 |
Let α, β be roots of the equation 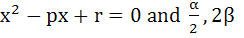 are the roots of the equation are the roots of the equation 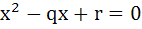 then the value of r is equal to then the value of r is equal to a) 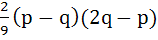 b) 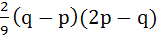 c) 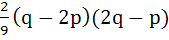 d) 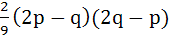
Let α, β be roots of the equation 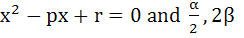 are the roots of the equation are the roots of the equation 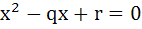 then the value of r is equal to then the value of r is equal to a) 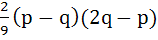 b) 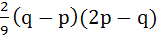 c) 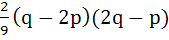 d) 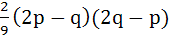
|
IIT 2007 |
02:46 min
|
|
354 |
Show that square of 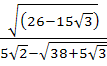 is a rational number. is a rational number.
Show that square of 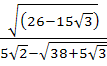 is a rational number. is a rational number.
|
IIT 1978 |
04:58 min
|
|
355 |
The determinants 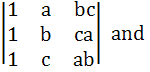 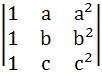 are. are. a) Identical b) Not identical c) Identical if a = b = c d) None of the above
The determinants 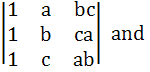 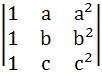 are. are. a) Identical b) Not identical c) Identical if a = b = c d) None of the above
|
IIT 1983 |
02:07 min
|
|
356 |
Given that x = −9 is a root of 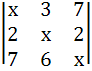 = 0 = 0  . .
a) {2, 7} b) {−2, −7} c) {2, 0} d) {0, 7}
Given that x = −9 is a root of 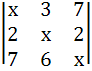 = 0 = 0  . .
a) {2, 7} b) {−2, −7} c) {2, 0} d) {0, 7}
|
IIT 1983 |
02:14 min
|
|
357 |
An ellipse has OB as a semi-minor axis. F, F’ are its focii and the angle FBF’ is a right angle. Then the eccentricity of the ellipse is . . . . .
An ellipse has OB as a semi-minor axis. F, F’ are its focii and the angle FBF’ is a right angle. Then the eccentricity of the ellipse is . . . . .
|
IIT 1997 |
02:22 min
|
|
358 |
If x = 9 is the chord of contact of the hyperbola 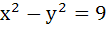 then the equation of the corresponding pair of tangents is then the equation of the corresponding pair of tangents is a) 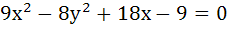 b) 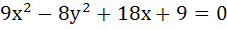 c) 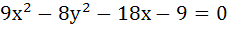 d) 
If x = 9 is the chord of contact of the hyperbola 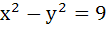 then the equation of the corresponding pair of tangents is then the equation of the corresponding pair of tangents is a) 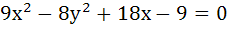 b) 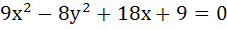 c) 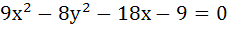 d) 
|
IIT 1999 |
03:20 min
|
|
359 |
Solve for x 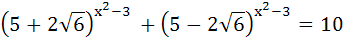
Solve for x 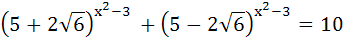
|
IIT 1985 |
03:54 min
|
|
360 |
The rational number which equals the numbers 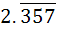 with recurring decimals is with recurring decimals is a) 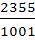 b) 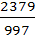 c) 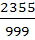 d) 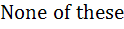
The rational number which equals the numbers 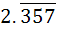 with recurring decimals is with recurring decimals is a) 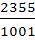 b) 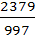 c) 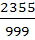 d) 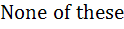
|
IIT 1983 |
02:26 min
|
|
361 |
(Fill in the blanks) The function y = 2x2 – ln|x| is monotonically increasing for values of x (≠0) satisfying the inequalities . . . . and monotonically decreasing for values of x satisfying the inequalities . . . . a) 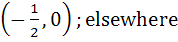 b) 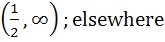 c) 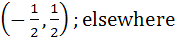 d) 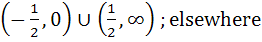
(Fill in the blanks) The function y = 2x2 – ln|x| is monotonically increasing for values of x (≠0) satisfying the inequalities . . . . and monotonically decreasing for values of x satisfying the inequalities . . . . a) 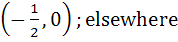 b) 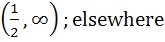 c) 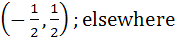 d) 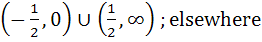
|
IIT 1983 |
04:07 min
|
|
362 |
Find 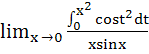 a) 0 b) 1 c) 2 d) 4
Find 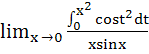 a) 0 b) 1 c) 2 d) 4
|
IIT 1997 |
02:33 min
|
|
363 |
The probability that an event A happens in one of the experiments is 0.4 Three independent trials of these experiments are performed. The probability that the event A happens at least once is a) 0.936 b) 0.784 c) 0.904 d) None of these
The probability that an event A happens in one of the experiments is 0.4 Three independent trials of these experiments are performed. The probability that the event A happens at least once is a) 0.936 b) 0.784 c) 0.904 d) None of these
|
IIT 1980 |
02:34 min
|
|
364 |
Let 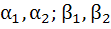 be roots of the equations be roots of the equations 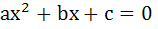 and and 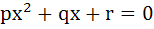 respectively. If the system of equations respectively. If the system of equations 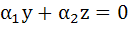 and and 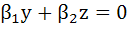 have non-trivial solutions then prove that have non-trivial solutions then prove that 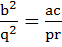
|
IIT 1987 |
05:52 min
|
|
365 |
If 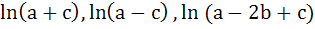 are in Arithmetic Progression are in Arithmetic Progression
then a) a, b, c are in Arithmetic Progression b) 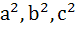 are in Arithmetic Progression are in Arithmetic Progression c) a, b, c are in Geometric Progression d) a, b, c are in Harmonic Progression
If 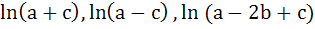 are in Arithmetic Progression are in Arithmetic Progression
then a) a, b, c are in Arithmetic Progression b) 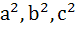 are in Arithmetic Progression are in Arithmetic Progression c) a, b, c are in Geometric Progression d) a, b, c are in Harmonic Progression
|
IIT 1994 |
02:24 min
|
|
366 |
Let f(x) = ∫ex (x – 1) (x − 2) dx, then f(x) decreases in the interval a) (−∞, −2) b) (−2, −1) c) (1, 2) d) (2, ∞)
Let f(x) = ∫ex (x – 1) (x − 2) dx, then f(x) decreases in the interval a) (−∞, −2) b) (−2, −1) c) (1, 2) d) (2, ∞)
|
IIT 2000 |
00:47 min
|
|
367 |
The harmonic means of the roots of the equation
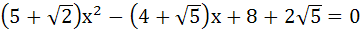 is is a) 2 b) 4 c) 6 d) 8
The harmonic means of the roots of the equation
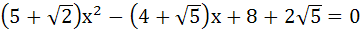 is is a) 2 b) 4 c) 6 d) 8
|
IIT 1999 |
01:43 min
|
|
368 |
Find the integral of 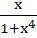 a) tan−1x2 + c b) 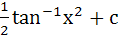 c) 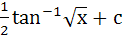 d) 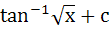
Find the integral of 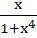 a) tan−1x2 + c b) 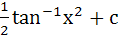 c) 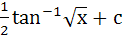 d) 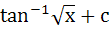
|
IIT 1978 |
00:32 min
|
|
369 |
Consider the two curves 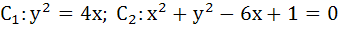 then then a) 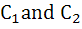 touch each other at only one point touch each other at only one point b) 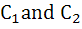 touch each other exactly at two points touch each other exactly at two points c) 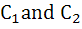 intersect(but not touch) at exactly two points intersect(but not touch) at exactly two points d) 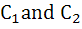 neither intersect nor touch each other neither intersect nor touch each other
Consider the two curves 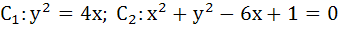 then then a) 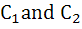 touch each other at only one point touch each other at only one point b) 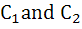 touch each other exactly at two points touch each other exactly at two points c) 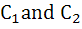 intersect(but not touch) at exactly two points intersect(but not touch) at exactly two points d) 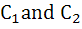 neither intersect nor touch each other neither intersect nor touch each other
|
IIT 2008 |
04:50 min
|
|
370 |
Suppose p(x) = 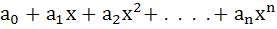
If 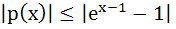 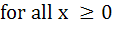 prove that prove that
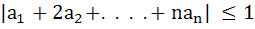
|
IIT 2000 |
05:19 min
|
|
371 |
The sum of the first 2n terms of the Arithmetic Progression 2, 5, 8, . . . . is equal to the sum of the first n terms of the Arithmetic Progression 57, 59, 61, . . . . then n equals a) 100 b) 12 c) 11 d) 13
The sum of the first 2n terms of the Arithmetic Progression 2, 5, 8, . . . . is equal to the sum of the first n terms of the Arithmetic Progression 57, 59, 61, . . . . then n equals a) 100 b) 12 c) 11 d) 13
|
IIT 2001 |
01:42 min
|
|
372 |
Show that 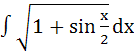 = = 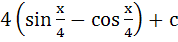
Show that 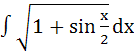 = = 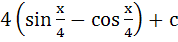
|
IIT 1980 |
01:51 min
|
|
373 |
Seven white balls and three black balls are randomly placed in a row. The possibility that no two black balls are placed adjacently equals a)  b) 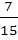 c) 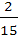 d) 
Seven white balls and three black balls are randomly placed in a row. The possibility that no two black balls are placed adjacently equals a)  b) 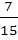 c) 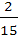 d) 
|
IIT 1998 |
03:25 min
|
|
374 |
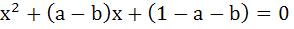 where a, b ε R then find the value of a for which equation has unequal roots for all values of b. where a, b ε R then find the value of a for which equation has unequal roots for all values of b.
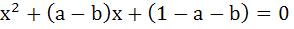 where a, b ε R then find the value of a for which equation has unequal roots for all values of b. where a, b ε R then find the value of a for which equation has unequal roots for all values of b.
|
IIT 2003 |
02:36 min
|
|
375 |
If α, β are roots of 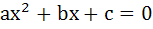 and and 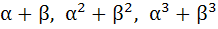 are in Geometric Progression and are in Geometric Progression and 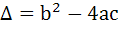 then then a) 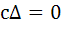 b) 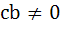 c) 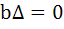 d) 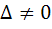
If α, β are roots of 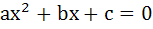 and and 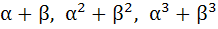 are in Geometric Progression and are in Geometric Progression and 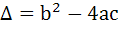 then then a) 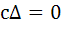 b) 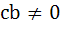 c) 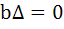 d) 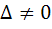
|
IIT 2005 |
02:38 min
|