|
1201 |
In a certain test 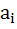 students gave wrong answers to at least i questions where i = 1, 2, …, k. No student gave more than k correct answers. Total number of wrong answers given is . . . students gave wrong answers to at least i questions where i = 1, 2, …, k. No student gave more than k correct answers. Total number of wrong answers given is . . .
In a certain test 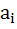 students gave wrong answers to at least i questions where i = 1, 2, …, k. No student gave more than k correct answers. Total number of wrong answers given is . . . students gave wrong answers to at least i questions where i = 1, 2, …, k. No student gave more than k correct answers. Total number of wrong answers given is . . .
|
IIT 1982 |
|
|
1202 |
Multiple choice If 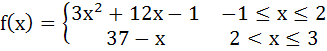 a) f(x) is increasing on [– 1, 2] b) f(x) is continuous on [– 1, 3] c) 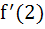 does not exist does not exist d) f(x) has maximum value at x = 2
Multiple choice If 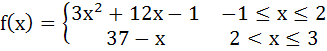 a) f(x) is increasing on [– 1, 2] b) f(x) is continuous on [– 1, 3] c) 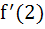 does not exist does not exist d) f(x) has maximum value at x = 2
|
IIT 1993 |
|
|
1203 |
If arg(z) < 0 then arg(−z) – arg(z) is equal to a) π b) –π c) – π/2 d) π/2
If arg(z) < 0 then arg(−z) – arg(z) is equal to a) π b) –π c) – π/2 d) π/2
|
IIT 2000 |
|
|
1204 |
Multiple choice f(x) is a cubic polynomial with f(2) = 18 and f(1) = − 1. Also f(x) has a local maxima at x = − 1 and 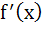 has a local minima at x = 0 then has a local minima at x = 0 then a) The distance between (− 1, 2) and (a, f(a)), where x = a is the point of local minimum, is 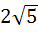 b) f(x) is increasing for 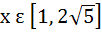 c) f(x) has a local minima at x = 1 d) The value of f(0) = 15
Multiple choice f(x) is a cubic polynomial with f(2) = 18 and f(1) = − 1. Also f(x) has a local maxima at x = − 1 and 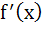 has a local minima at x = 0 then has a local minima at x = 0 then a) The distance between (− 1, 2) and (a, f(a)), where x = a is the point of local minimum, is 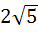 b) f(x) is increasing for 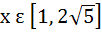 c) f(x) has a local minima at x = 1 d) The value of f(0) = 15
|
IIT 2006 |
|
|
1205 |
From the point A (0, 3) on the circle 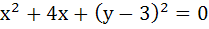 , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . . , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . .
From the point A (0, 3) on the circle 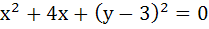 , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . . , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . .
|
IIT 1986 |
|
|
1206 |
In Δ ABC the median to the side BC is of length 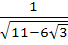 and divides ∠A into 30° and 45°. Then find the length of side BC. and divides ∠A into 30° and 45°. Then find the length of side BC. a) 1 b) 2 c) 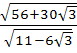 d) 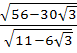
In Δ ABC the median to the side BC is of length 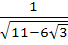 and divides ∠A into 30° and 45°. Then find the length of side BC. and divides ∠A into 30° and 45°. Then find the length of side BC. a) 1 b) 2 c) 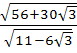 d) 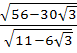
|
IIT 1985 |
|
|
1207 |
If f is an even function defined on (−5, 5) then the real values of x satisfying the equation f (x) = 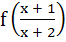 are …………… are …………… a) 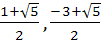 b) 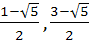 c) 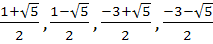 d) 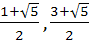
If f is an even function defined on (−5, 5) then the real values of x satisfying the equation f (x) = 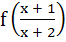 are …………… are …………… a) 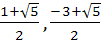 b) 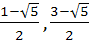 c) 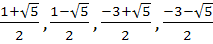 d) 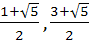
|
IIT 1996 |
|
|
1208 |
If ω(≠1) be a cube root of unity and 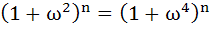 then the least positive value of n is then the least positive value of n is a) 2 b) 3 c) 5 d) 6
If ω(≠1) be a cube root of unity and 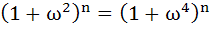 then the least positive value of n is then the least positive value of n is a) 2 b) 3 c) 5 d) 6
|
IIT 2004 |
|
|
1209 |
A circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in the circle is . . . . .
A circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in the circle is . . . . .
|
IIT 1994 |
|
|
1210 |
The number of all possible triplets 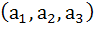 such that such that
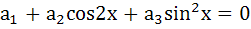 for all x is for all x is a) Zero b) One c) Three d) Infinite e) None
The number of all possible triplets 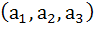 such that such that
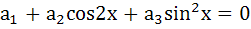 for all x is for all x is a) Zero b) One c) Three d) Infinite e) None
|
IIT 1987 |
|
|
1211 |
A swimmer S is in the sea at a distance d km. from the closest point A on a straight shore. The house of the swimmer is on the shore at a distance L km. from A. He can swim at a speed of
u km/hour and walk at a speed of v km/hr (v > u). At what point on the shore should he land so that he reaches his house in the shortest possible time. a) 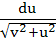 b) 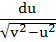 c) 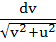 d) 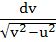
A swimmer S is in the sea at a distance d km. from the closest point A on a straight shore. The house of the swimmer is on the shore at a distance L km. from A. He can swim at a speed of
u km/hour and walk at a speed of v km/hr (v > u). At what point on the shore should he land so that he reaches his house in the shortest possible time. a) 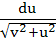 b) 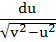 c) 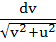 d) 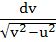
|
IIT 1983 |
|
|
1212 |
Sketch the region bounded by the curves
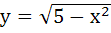 and y = |x – 1| and y = |x – 1|
and find its area. a) 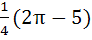 b) 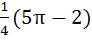 c) 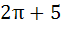 d) 5π + 2
Sketch the region bounded by the curves
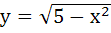 and y = |x – 1| and y = |x – 1|
and find its area. a) 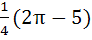 b) 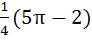 c) 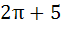 d) 5π + 2
|
IIT 1985 |
|
|
1213 |
Tangents are drawn from the point (17, 7) to the circle 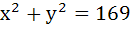 . .
Statement 1 – The tangents are mutually perpendicular, because Statement 2 – The locus of points from which mutually perpendicular tangents are drawn to the given circle is 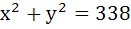 . . The question contains statement – 1 (assertion) and statement 2 (reason). Of these statements mark correct choice if a) Statement 1 and 2 are true. Statement 2 is a correct explanation for statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation for statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true
Tangents are drawn from the point (17, 7) to the circle 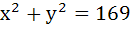 . .
Statement 1 – The tangents are mutually perpendicular, because Statement 2 – The locus of points from which mutually perpendicular tangents are drawn to the given circle is 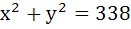 . . The question contains statement – 1 (assertion) and statement 2 (reason). Of these statements mark correct choice if a) Statement 1 and 2 are true. Statement 2 is a correct explanation for statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation for statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true
|
IIT 2007 |
|
|
1214 |
Let 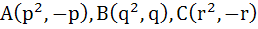 be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. a) 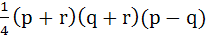 b) 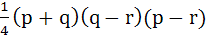 c) 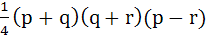 d) 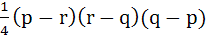
Let 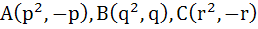 be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. a) 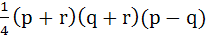 b) 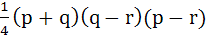 c) 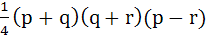 d) 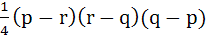
|
IIT 1986 |
|
|
1215 |
Two rays in the first quadrant x + y = |a| and ax – y = 1 intersect each other in the interval a ε (a0, ∞). The value of a0 is
Two rays in the first quadrant x + y = |a| and ax – y = 1 intersect each other in the interval a ε (a0, ∞). The value of a0 is
|
IIT 2006 |
|
|
1216 |
Find the area of the region bounded by the curve C: y = tanx, tangent drawn to C at 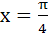 and the X–axis. and the X–axis. a) ln2 – 1 b) 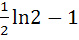 c) 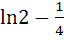 d) 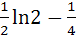
Find the area of the region bounded by the curve C: y = tanx, tangent drawn to C at 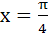 and the X–axis. and the X–axis. a) ln2 – 1 b) 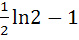 c) 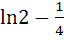 d) 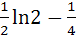
|
IIT 1988 |
|
|
1217 |
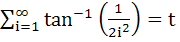 then tan t = then tan t =
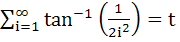 then tan t = then tan t =
|
IIT 2006 |
|
|
1218 |
Sketch the curves and identify the region bounded by
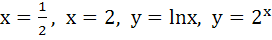
Sketch the curves and identify the region bounded by
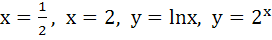
|
IIT 1991 |
|
|
1219 |
Consider the following linear equations
ax + by + cz = 0
bx + cy + az = 0
cx + ay + bz = 0
Match the statements/expressions in column 1 with column 2
| Column 1 | Column2 | | i. a + b + c ≠ 0 and a2 + b2 + c2 = ab + bc + ca | A. Equations represent planes meeting at only one single point | | ii. a + b + c = 0 and a2 + b2 + c2 ≠ ab + bc + ca | B. The equations represent the line x = y = z | | iii. a + b + c ≠ 0 and a2 + b2 + c2 ≠ ab + bc + ca | C. The equations represent identical planes | | iv. a + b + c = 0 and a2 + b2 + c2 = ab + bc + ca | D.The equations represent the whole of the three dimensional space |
Consider the following linear equations
ax + by + cz = 0
bx + cy + az = 0
cx + ay + bz = 0
Match the statements/expressions in column 1 with column 2
| Column 1 | Column2 | | i. a + b + c ≠ 0 and a2 + b2 + c2 = ab + bc + ca | A. Equations represent planes meeting at only one single point | | ii. a + b + c = 0 and a2 + b2 + c2 ≠ ab + bc + ca | B. The equations represent the line x = y = z | | iii. a + b + c ≠ 0 and a2 + b2 + c2 ≠ ab + bc + ca | C. The equations represent identical planes | | iv. a + b + c = 0 and a2 + b2 + c2 = ab + bc + ca | D.The equations represent the whole of the three dimensional space |
|
IIT 2007 |
|
|
1220 |
The domain of the function y(x) given by the equation 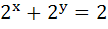 is is a) 0 < x ≤ 1 b) 0 ≤ x ≤ 1 c) 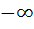 < x ≤ 0 < x ≤ 0 d) 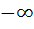 < x < 1 < x < 1
The domain of the function y(x) given by the equation 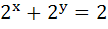 is is a) 0 < x ≤ 1 b) 0 ≤ x ≤ 1 c) 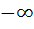 < x ≤ 0 < x ≤ 0 d) 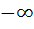 < x < 1 < x < 1
|
IIT 2000 |
|
|
1221 |
If A =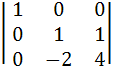 , 6A-1 = A2 + cA + dI , 6A-1 = A2 + cA + dI then (c, d ) is a) (−11, 6) b) (−6, 11) c) (6, 11 ) d) (11, 6 )
If A =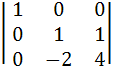 , 6A-1 = A2 + cA + dI , 6A-1 = A2 + cA + dI then (c, d ) is a) (−11, 6) b) (−6, 11) c) (6, 11 ) d) (11, 6 )
|
IIT 2005 |
|
|
1222 |
Prove that 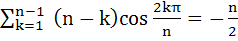
Prove that 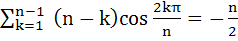
|
IIT 1997 |
|
|
1223 |
Tangent at a point P1 (other than (10, 0)) on the curve y = x3 meets the curve again at P2. The tangent at P2 meets the curve at P3 and so on. Show that the abscissae of P1, P2, P3, . . . , Pn form a Geometric Progression. Also find the ratio 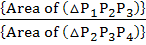 . . a) 32 b) 16 c) 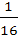 d) 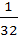
Tangent at a point P1 (other than (10, 0)) on the curve y = x3 meets the curve again at P2. The tangent at P2 meets the curve at P3 and so on. Show that the abscissae of P1, P2, P3, . . . , Pn form a Geometric Progression. Also find the ratio 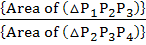 . . a) 32 b) 16 c) 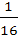 d) 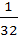
|
IIT 1993 |
|
|
1224 |
In what ratio does the X–axis divide the area of the region bounded by the parabolas y = 4x – x2 and y = x2 – x a) 1:4 b) 21:1 c) 21:4 d) 3:4
In what ratio does the X–axis divide the area of the region bounded by the parabolas y = 4x – x2 and y = x2 – x a) 1:4 b) 21:1 c) 21:4 d) 3:4
|
IIT 1994 |
|
|
1225 |
Let C1 and C2, be respectively, the parabolas 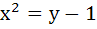 and and 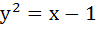 . Let P be any point on C1 and Q be any point on C2. Let P1 and Q1 be the reflections of P and Q respectively with respect to y = x . Prove that P1 lies on C2 and Q1 lies on C1 and . Let P be any point on C1 and Q be any point on C2. Let P1 and Q1 be the reflections of P and Q respectively with respect to y = x . Prove that P1 lies on C2 and Q1 lies on C1 and 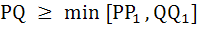 . Hence or otherwise determine points P2 and Q2 on the parabolas C1 and C2 respectively such that . Hence or otherwise determine points P2 and Q2 on the parabolas C1 and C2 respectively such that 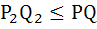 for all points (P, Q) with P on C1 and Q on C2 . for all points (P, Q) with P on C1 and Q on C2 .
|
IIT 2000 |
|