|
951 |
Let f: [0, 2] → ℝ be a function which is continuous on [0, 2] and differentiable on (0, 2) with f(0) = 1. Let F(x)=x2∫0f(√t)dtforx∈[0,2] . If F′(x) = f′(x) Ɐ x ∈ [0, 2] then F(2) equals a) e2 – 1 b) e4 – 1 c) e – 1 d) e2
Let f: [0, 2] → ℝ be a function which is continuous on [0, 2] and differentiable on (0, 2) with f(0) = 1. Let F(x)=x2∫0f(√t)dtforx∈[0,2] . If F′(x) = f′(x) Ɐ x ∈ [0, 2] then F(2) equals a) e2 – 1 b) e4 – 1 c) e – 1 d) e2
|
IIT 2014 |
|
|
952 |
(Multiple correct answers) Let M and N are two events, the probability that exactly one of them occurs is a) P (M) + P (N) − 2P (M ∩ N) b) P (M) + P (N) − P ( ) ) c)  d) 
(Multiple correct answers) Let M and N are two events, the probability that exactly one of them occurs is a) P (M) + P (N) − 2P (M ∩ N) b) P (M) + P (N) − P ( ) ) c)  d) 
|
IIT 1984 |
|
|
953 |
The area (in square units) of the region y2 > 2x and x2 + y2 ≤ 4x, x ≥ 0, y > 0 is a) π−43 b) π−83 c) π−4√23 d) π2−2√23
The area (in square units) of the region y2 > 2x and x2 + y2 ≤ 4x, x ≥ 0, y > 0 is a) π−43 b) π−83 c) π−4√23 d) π2−2√23
|
IIT 2016 |
|
|
954 |
Let f and g be real valued functions on (−1, 1) such that g’(x) is continuous, g(0) ≠ 0, g’(0) = 0, g’’(0) ≠ 0 and f(x) = g(x)sinx
Statement 1 - 
Statement 2 – f’(0) = g(0) a) Statement 1 is true. Statement 2 is true. Statement 2 is a correct explanation of statement 1 b) Statement 1 is true. Statement 2 is true. Statement 2 is not a correct explanation of statement 1 c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
Let f and g be real valued functions on (−1, 1) such that g’(x) is continuous, g(0) ≠ 0, g’(0) = 0, g’’(0) ≠ 0 and f(x) = g(x)sinx
Statement 1 - 
Statement 2 – f’(0) = g(0) a) Statement 1 is true. Statement 2 is true. Statement 2 is a correct explanation of statement 1 b) Statement 1 is true. Statement 2 is true. Statement 2 is not a correct explanation of statement 1 c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
|
IIT 2008 |
|
|
955 |
The area of the region {(x,y)∈R2:y>√|x+3|,5y≤x+9≤15} is equal to a) 16 b) 43 c) 32 d) 53
The area of the region {(x,y)∈R2:y>√|x+3|,5y≤x+9≤15} is equal to a) 16 b) 43 c) 32 d) 53
|
IIT 2016 |
|
|
956 |
The area (in square units) bounded by the curves y=√x,2y−x+3=0 , X – axis and lying in the first quadrant is a) 9 b) 6 c) 18 d) 274
The area (in square units) bounded by the curves y=√x,2y−x+3=0 , X – axis and lying in the first quadrant is a) 9 b) 6 c) 18 d) 274
|
IIT 2013 |
|
|
957 |
One or more than one correct option Let S be the area of the region enclosed by y=e−x2 , y = 0, x = 0 and x = 1, then a) S≥1e b) S≥1−1e c) S≤14(1+1√e) d) S≤1√2+1√e(1−1√2)
One or more than one correct option Let S be the area of the region enclosed by y=e−x2 , y = 0, x = 0 and x = 1, then a) S≥1e b) S≥1−1e c) S≤14(1+1√e) d) S≤1√2+1√e(1−1√2)
|
IIT 2012 |
|
|
958 |
Show that the sum of the first n terms of the series
12 + 2.22 + 32 + 2.42 + 52 + 2.62 + . . .
is 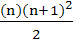 when n is even, and when n is even, and 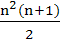 when n is odd. when n is odd.
Show that the sum of the first n terms of the series
12 + 2.22 + 32 + 2.42 + 52 + 2.62 + . . .
is 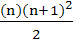 when n is even, and when n is even, and 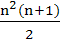 when n is odd. when n is odd.
|
IIT 1988 |
|
|
959 |
Differentiate from first principles (or ab initio)  a) 2xcos(x2 + 1) b) xcos(x2 + 1) c) 2cosx(x2 + 1) d) 2xcosx(x2 + 1) + sin(x2 + 1)
Differentiate from first principles (or ab initio)  a) 2xcos(x2 + 1) b) xcos(x2 + 1) c) 2cosx(x2 + 1) d) 2xcosx(x2 + 1) + sin(x2 + 1)
|
IIT 1978 |
|
|
960 |
One or more than one correct option Let y(x) be a solution of the differential equation (1+ex)y′+yex=1 . If y(0) = 2, then which of the following statements is/are true? a) y(−4) = 0 b) y(−2) = 0 c) y(x) has a critical point in the interval (−1, 0) d) y(x) has no critical point in the interval
One or more than one correct option Let y(x) be a solution of the differential equation (1+ex)y′+yex=1 . If y(0) = 2, then which of the following statements is/are true? a) y(−4) = 0 b) y(−2) = 0 c) y(x) has a critical point in the interval (−1, 0) d) y(x) has no critical point in the interval
|
IIT 2015 |
|
|
961 |
An urn contains two white and two black balls. A ball is drawn at random. If it is white it is not replaced in the urn. Otherwise it is placed along with the other balls of the same colour. The process is repeated. Find the probability that the third ball drawn is black?
An urn contains two white and two black balls. A ball is drawn at random. If it is white it is not replaced in the urn. Otherwise it is placed along with the other balls of the same colour. The process is repeated. Find the probability that the third ball drawn is black?
|
IIT 1987 |
|
|
962 |
Find the derivative with respect to x of the function 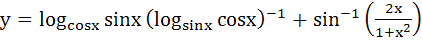 at x = at x =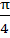
a) 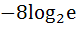 b) 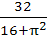 c) 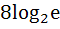 d) 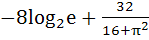
Find the derivative with respect to x of the function 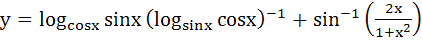 at x = at x =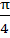
a) 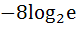 b) 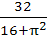 c) 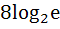 d) 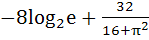
|
IIT 1984 |
|
|
963 |
The function y = f(x) is the solution of the differential equation dydx+xyx2−1=x4+2x√1−x2 in (−1, 1) satisfying f(0) = 0, then √32∫−√32f(x)dx is a) π3−√32 b) π3−√34 c) π6−√34 d) π6−√32
The function y = f(x) is the solution of the differential equation dydx+xyx2−1=x4+2x√1−x2 in (−1, 1) satisfying f(0) = 0, then √32∫−√32f(x)dx is a) π3−√32 b) π3−√34 c) π6−√34 d) π6−√32
|
IIT 2014 |
|
|
964 |
Solve 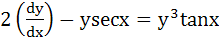
Solve 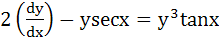
|
IIT 1996 |
|
|
965 |
Let y′(x) + y(x) g′(x) = g(x) g′(x), y(0) = 0, x ∈ ℝ where f′(x) denotes ddxf(x) and g(x) is a given non constant differentiable function on ℝ with g(0) = g(2) = 0. Then the value of y(2) is a) 1 b) 0 c) 2 d) 4
Let y′(x) + y(x) g′(x) = g(x) g′(x), y(0) = 0, x ∈ ℝ where f′(x) denotes ddxf(x) and g(x) is a given non constant differentiable function on ℝ with g(0) = g(2) = 0. Then the value of y(2) is a) 1 b) 0 c) 2 d) 4
|
IIT 2011 |
|
|
966 |
One or more than one correct option A solution curve of the differential equation (x2+xy+4x+2y+4)dydx−y2=0,x>0 passes through the point (1, 3), then the solution curve a) Intersects y = x + 2 exactly at one point b) Intersects y = x + 2 exactly at two points c) Intersects y = (x + 2)2 d) Does not intersect y = (x + 3)2
One or more than one correct option A solution curve of the differential equation (x2+xy+4x+2y+4)dydx−y2=0,x>0 passes through the point (1, 3), then the solution curve a) Intersects y = x + 2 exactly at one point b) Intersects y = x + 2 exactly at two points c) Intersects y = (x + 2)2 d) Does not intersect y = (x + 3)2
|
IIT 2016 |
|
|
967 |
The value of 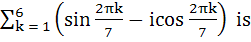 a) –1 b) 0 c) 1 d) i e) None of these
The value of 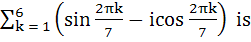 a) –1 b) 0 c) 1 d) i e) None of these
|
IIT 1987 |
|
|
968 |
Let U1 = 1, U2 = 1, Un + 2 = Un + 1 + Un, n > 1. Use mathematical induction to show that
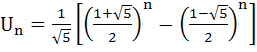
for all integers n > 1
Let U1 = 1, U2 = 1, Un + 2 = Un + 1 + Un, n > 1. Use mathematical induction to show that
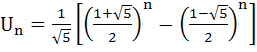
for all integers n > 1
|
IIT 1981 |
|
|
969 |
Let f(x) = (1 – x)2 sin2x + x2Consider the statementsStatement 1: There exists some x ∈ ℝ such that f(x) + 2x = 2(1 + x2)Statement 2: There exists some x ∈ ℝ such that 2f(x) + 1 = 2x(x + 1) a) Both 1 and 2 are true b) 1 is true and 2 is false c) 1 is false and 2 is true d) Both 1 and 2 are false
Let f(x) = (1 – x)2 sin2x + x2Consider the statementsStatement 1: There exists some x ∈ ℝ such that f(x) + 2x = 2(1 + x2)Statement 2: There exists some x ∈ ℝ such that 2f(x) + 1 = 2x(x + 1) a) Both 1 and 2 are true b) 1 is true and 2 is false c) 1 is false and 2 is true d) Both 1 and 2 are false
|
IIT 2013 |
|
|
970 |
Let z and ω be two complex numbers such that |z| ≤ 1, |ω| ≤ 1 and 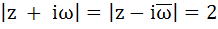 then z equals then z equals a) 1 or i b) i or –i c) 1 or –1 d) i or –1
Let z and ω be two complex numbers such that |z| ≤ 1, |ω| ≤ 1 and 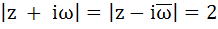 then z equals then z equals a) 1 or i b) i or –i c) 1 or –1 d) i or –1
|
IIT 1995 |
|
|
971 |
Given
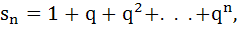 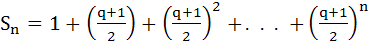
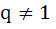
Prove that
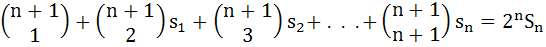
|
IIT 1984 |
|
|
972 |
The coordinates of the in centre of the triangle that has the co ordinates of the mid points of its sides as (0, 1), (1, 1) and (1, 0) is a) 2+√2 b) 2−√2 c) 1+√2 d) 1−√2
The coordinates of the in centre of the triangle that has the co ordinates of the mid points of its sides as (0, 1), (1, 1) and (1, 0) is a) 2+√2 b) 2−√2 c) 1+√2 d) 1−√2
|
IIT 2013 |
|
|
973 |
Using mathematical induction, prove that 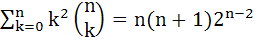 for n > 1 for n > 1
Using mathematical induction, prove that 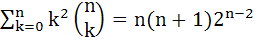 for n > 1 for n > 1
|
IIT 1986 |
|
|
974 |
If f(x) = 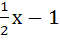 then on the interval [0, π] then on the interval [0, π] a) tan 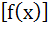 and and 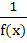 are both continuous are both continuous b) tan 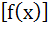 and and 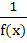 are both discontinuous are both discontinuous c) tan 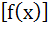 and and 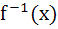 are both continuous are both continuous d) tan 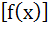 is continuous but is continuous but 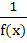 is not is not
|
IIT 1989 |
|
|
975 |
One or more than one correct option A ray of light along x+√3y=√3 gets reflected upon reaching X- axis, the equation of the reflected ray is a) y=x+√3 b) √3y=x−√3 c) y=√3x−√3 d) √3y=x−1
One or more than one correct option A ray of light along x+√3y=√3 gets reflected upon reaching X- axis, the equation of the reflected ray is a) y=x+√3 b) √3y=x−√3 c) y=√3x−√3 d) √3y=x−1
|
IIT 2013 |
|