|
901 |
Tangents are drawn to the circle 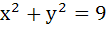 from a point on the hyperbola from a point on the hyperbola 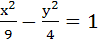 . Find the locus of the midpoint of the chord of contact. . Find the locus of the midpoint of the chord of contact.
Tangents are drawn to the circle 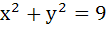 from a point on the hyperbola from a point on the hyperbola 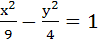 . Find the locus of the midpoint of the chord of contact. . Find the locus of the midpoint of the chord of contact.
|
IIT 2005 |
|
|
902 |
The value of the integral π/2∫−π/2(x2+logπ−xπ+x)cosxdx is equal to a) 0 b) π22−4 c) π22+4 d) π22
The value of the integral π/2∫−π/2(x2+logπ−xπ+x)cosxdx is equal to a) 0 b) π22−4 c) π22+4 d) π22
|
IIT 2012 |
|
|
903 |
Show that the integral of sinxsin2xsin3x + sec2xcos22x + sin4xcos4x is 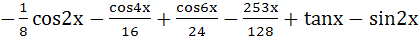
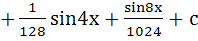
Show that the integral of sinxsin2xsin3x + sec2xcos22x + sin4xcos4x is 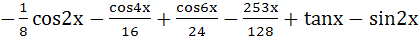
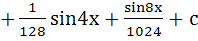
|
IIT 1979 |
|
|
904 |
Let P (x1, y1) and Q (x2, y2), y1 < 0, y2 < 0 be the end points of the latus rectum of the ellipse x2 + 4y2 = 4. The equations of the parabolas with latus rectum PQ are a) 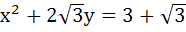 b) 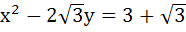 c) 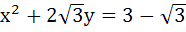 d) 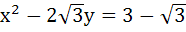
Let P (x1, y1) and Q (x2, y2), y1 < 0, y2 < 0 be the end points of the latus rectum of the ellipse x2 + 4y2 = 4. The equations of the parabolas with latus rectum PQ are a) 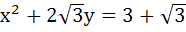 b) 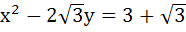 c) 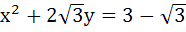 d) 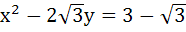
|
IIT 2008 |
|
|
905 |
Let F : ℝ → ℝ be a thrice differentiable function. Suppose that F(1) = 0, F(3) = −4 and F′(x) < 0 for all x ε (1, 3). Let f(x) = x F(x) for all x ε ℝ.If 3∫1x2F′(x)dx=−12 and 3∫1x3F′′(x)dx=40 , then the correct expression is/are a) 9f′(3)+f′(1)−32=0 b) 3∫1f(x)dx=12 c) 9f′(3)−f′(1)+32=0 d) 3∫1f(x)dx=−12
Let F : ℝ → ℝ be a thrice differentiable function. Suppose that F(1) = 0, F(3) = −4 and F′(x) < 0 for all x ε (1, 3). Let f(x) = x F(x) for all x ε ℝ.If 3∫1x2F′(x)dx=−12 and 3∫1x3F′′(x)dx=40 , then the correct expression is/are a) 9f′(3)+f′(1)−32=0 b) 3∫1f(x)dx=12 c) 9f′(3)−f′(1)+32=0 d) 3∫1f(x)dx=−12
|
IIT 2015 |
|
|
906 |
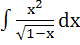 = =
a) 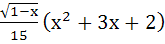 +c +c b) 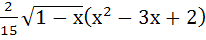 +c +c c) 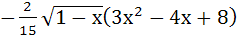 +c +c d) 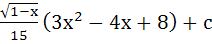
|
IIT 1980 |
|
|
907 |
Consider the points
P: (−sin (β – α), 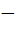 cosβ) cosβ)
Q: (cos (β – α), sinβ)
R: (−cos{(β – α) + θ}, sin (β – θ))
where 0 < α, β, θ < 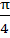 then then a) P lies on the line segment RQ b) Q lies on the line segment PR c) R lies on the line segment QP d) P, Q, R are non–collinear
Consider the points
P: (−sin (β – α), 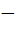 cosβ) cosβ)
Q: (cos (β – α), sinβ)
R: (−cos{(β – α) + θ}, sin (β – θ))
where 0 < α, β, θ < 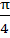 then then a) P lies on the line segment RQ b) Q lies on the line segment PR c) R lies on the line segment QP d) P, Q, R are non–collinear
|
IIT 2008 |
|
|
908 |
One or more than one correct options The options with the values of α and L that satisfy the equation 4π∫0et[sin6αt+cos4αt]dtπ∫0et[sin6αt+cos4αt]dt=L is/are a) α=2,L=e4π−1eπ−1 b) α=2,L=e4π+1eπ+1 c) α=4,L=e4π−1eπ−1 d) α=4,L=e4π+1eπ+1
One or more than one correct options The options with the values of α and L that satisfy the equation 4π∫0et[sin6αt+cos4αt]dtπ∫0et[sin6αt+cos4αt]dt=L is/are a) α=2,L=e4π−1eπ−1 b) α=2,L=e4π+1eπ+1 c) α=4,L=e4π−1eπ−1 d) α=4,L=e4π+1eπ+1
|
IIT 2010 |
|
|
909 |
The number of points in the interval [−√13,√13] in which f(x)=sin(x2)+cos(x2) attains its maximum value is a) 8 b) 2 c) 4 d) 0
The number of points in the interval [−√13,√13] in which f(x)=sin(x2)+cos(x2) attains its maximum value is a) 8 b) 2 c) 4 d) 0
|
IIT 2014 |
|
|
910 |
If the integers m and n are chosen at random between 1 and 100 then the probability that a number of form 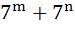 is divisible by 5, equals is divisible by 5, equals a)  b)  c)  d) 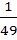
If the integers m and n are chosen at random between 1 and 100 then the probability that a number of form 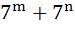 is divisible by 5, equals is divisible by 5, equals a)  b)  c)  d) 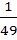
|
IIT 1999 |
|
|
911 |
Show that the integral
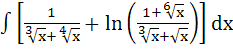 = = 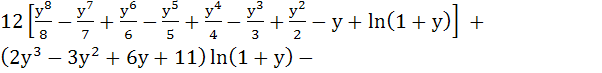
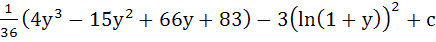
where y = x1/6
Show that the integral
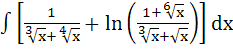 = = 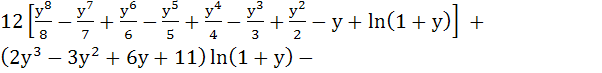
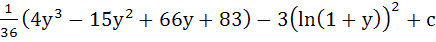
where y = x1/6
|
IIT 1992 |
|
|
912 |
If α=1∫0e(9x+3tan−1x)(12+9x21+x2)dx Where tan−1x takes only principal values then the value of (loge|1+α|−3π4) is a) 6 b) 9 c) 8 d) 11
If α=1∫0e(9x+3tan−1x)(12+9x21+x2)dx Where tan−1x takes only principal values then the value of (loge|1+α|−3π4) is a) 6 b) 9 c) 8 d) 11
|
IIT 2015 |
|
|
913 |
The intercept on X axis made by the tangent to the curve y=x∫0|t|dt,t∈R which is parallel to the line y = 2x are equal to a) ±1 b) ±2 c) ±3 d) ±4
The intercept on X axis made by the tangent to the curve y=x∫0|t|dt,t∈R which is parallel to the line y = 2x are equal to a) ±1 b) ±2 c) ±3 d) ±4
|
IIT 2013 |
|
|
914 |
The common tangent to the curve x2 + y2 = 2 and the parabola y2 = 8x touch the circle at the points P, Q and the parabola at the points R, S. Then the area (in square units) of the quadrilateral PQRS is a) 3 b) 6 c) 9 d) 15
The common tangent to the curve x2 + y2 = 2 and the parabola y2 = 8x touch the circle at the points P, Q and the parabola at the points R, S. Then the area (in square units) of the quadrilateral PQRS is a) 3 b) 6 c) 9 d) 15
|
IIT 2014 |
|
|
915 |
(One or more correct answers)
Let 0 < P (A) < 1, 0 < P (B) < 1 and P (A ∪ B) = P (A) + P (B) – P (A ∩ B) then a) P (B/A) = P (B) – P (A) b) P (Aʹ – Bʹ) = P (Aʹ) – P (Bʹ) c) P (A U B)ʹ = P (Aʹ) P (Bʹ) d) P (A/B) = P (A)
(One or more correct answers)
Let 0 < P (A) < 1, 0 < P (B) < 1 and P (A ∪ B) = P (A) + P (B) – P (A ∩ B) then a) P (B/A) = P (B) – P (A) b) P (Aʹ – Bʹ) = P (Aʹ) – P (Bʹ) c) P (A U B)ʹ = P (Aʹ) P (Bʹ) d) P (A/B) = P (A)
|
IIT 1995 |
|
|
916 |
For any integer n, the integral
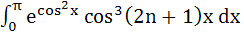 has the value has the value a) π b) 1 c) 0 d) None of these
For any integer n, the integral
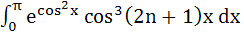 has the value has the value a) π b) 1 c) 0 d) None of these
|
IIT 1985 |
|
|
917 |
The area (in square units) of the region described by (x, y) : y2 < 2x and y ≥ 4x – 1 is a) 732 b) 932 c) 32 d) 53
The area (in square units) of the region described by (x, y) : y2 < 2x and y ≥ 4x – 1 is a) 732 b) 932 c) 32 d) 53
|
IIT 2015 |
|
|
918 |
Let f: [−1, 2] → [0, ∞) be a continuous function such that f(x) = f(1 –x), Ɐ x ∈ [−1, 2]. If R1=2∫−1xf(x)dx and R2 are the area of the region bounded by y = f(x), x = −1, x = 2 and the X- axis. Then a) R1 = 2R2 b) R1 = 3R2 c) 2R1 = R2 d) 3R1 = R2
Let f: [−1, 2] → [0, ∞) be a continuous function such that f(x) = f(1 –x), Ɐ x ∈ [−1, 2]. If R1=2∫−1xf(x)dx and R2 are the area of the region bounded by y = f(x), x = −1, x = 2 and the X- axis. Then a) R1 = 2R2 b) R1 = 3R2 c) 2R1 = R2 d) 3R1 = R2
|
IIT 2011 |
|
|
919 |
If (2+sinx)dydx+(y+1)cosx=0∧y(0)=1 , then y(π2) is equal to a) 13 b) −23 c) −13 d) 43
If (2+sinx)dydx+(y+1)cosx=0∧y(0)=1 , then y(π2) is equal to a) 13 b) −23 c) −13 d) 43
|
IIT 2017 |
|
|
920 |
One or more than one correct option Consider the family of circles whose centre lies on the straight line y = x. If the family of circles is represented by the differential equation Py′′ + Qy′ + 1 = 0 where P, Q are functions of x, y and y′ (wherey′=dydx,y′′=d2ydx2) , then which of the following statements is/are true? a) P = y + x b) P = y – x c) P + Q = 1 – x + y + y′ + (y′)2 d) P − Q = x + y − y′ − (y′)2
One or more than one correct option Consider the family of circles whose centre lies on the straight line y = x. If the family of circles is represented by the differential equation Py′′ + Qy′ + 1 = 0 where P, Q are functions of x, y and y′ (wherey′=dydx,y′′=d2ydx2) , then which of the following statements is/are true? a) P = y + x b) P = y – x c) P + Q = 1 – x + y + y′ + (y′)2 d) P − Q = x + y − y′ − (y′)2
|
IIT 2015 |
|
|
921 |
Find 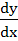 at x = at x = 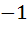 , when , when 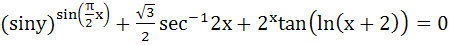
a) 0 b) 1 c) – 1 d) 2
Find 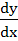 at x = at x = 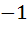 , when , when 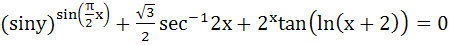
a) 0 b) 1 c) – 1 d) 2
|
IIT 1991 |
|
|
922 |
Let f : (0, ∞) → ℝ and 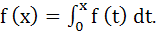 If If 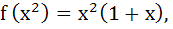 then f(4) equals then f(4) equals a)  b) 7 c) 4 d) 2
Let f : (0, ∞) → ℝ and 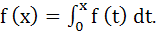 If If 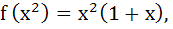 then f(4) equals then f(4) equals a)  b) 7 c) 4 d) 2
|
IIT 2001 |
|
|
923 |
Let f:[12,1]→R (the set of all real numbers) be a positive, non-constant and differentiable function such that f′(x)<2f(x) and f(12)=1 . Then the value of 1∫1/2f(x)dx lies in the interval a) (2e-1,2e) b) (e−1,2e-1) c) (e−12,e−1) d) (0,e−12)
Let f:[12,1]→R (the set of all real numbers) be a positive, non-constant and differentiable function such that f′(x)<2f(x) and f(12)=1 . Then the value of 1∫1/2f(x)dx lies in the interval a) (2e-1,2e) b) (e−1,2e-1) c) (e−12,e−1) d) (0,e−12)
|
IIT 2013 |
|
|
924 |
The smallest positive integer n for which 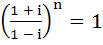 is is a) 8 b) 12 c) 12 d) None of these
The smallest positive integer n for which 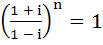 is is a) 8 b) 12 c) 12 d) None of these
|
IIT 1980 |
|
|
925 |
Let the population of rabbits arriving at time t be governed by the differential equation dp(t)dt=12p(t)−200 . If p(0) = 100, then p(t) is equal to a) 400 – 300et/2 b) 300 – 200e−t/2 c) 600 – 500et/2 d) 400 – 300e−t/2
Let the population of rabbits arriving at time t be governed by the differential equation dp(t)dt=12p(t)−200 . If p(0) = 100, then p(t) is equal to a) 400 – 300et/2 b) 300 – 200e−t/2 c) 600 – 500et/2 d) 400 – 300e−t/2
|
IIT 2014 |
|