|
876 |
Let n be an odd integer. If sin nθ = 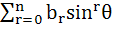 for every value of θ, then for every value of θ, then a) 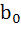 = 1, = 1, 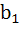 = 3 = 3 b) 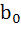 = 0, = 0, 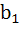 = n = n c) 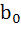 = −1, = −1, 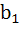 = n = n d) 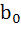 = 1, = 1, 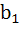 = = 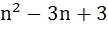
|
IIT 1998 |
|
|
877 |
The points with position vectors 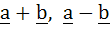 and and 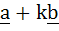 are collinear for all real values of k. are collinear for all real values of k. a) True b) False
The points with position vectors 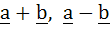 and and 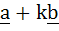 are collinear for all real values of k. are collinear for all real values of k. a) True b) False
|
IIT 1984 |
|
|
878 |
Multiple choices
Let 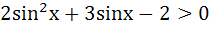 and and 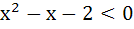 (x is measured in radians) then x lies in the interval (x is measured in radians) then x lies in the interval a) 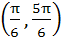 b) 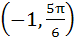 c) 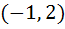 d) 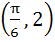
Multiple choices
Let 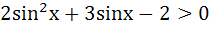 and and 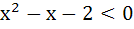 (x is measured in radians) then x lies in the interval (x is measured in radians) then x lies in the interval a) 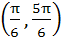 b) 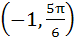 c) 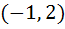 d) 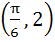
|
IIT 1994 |
|
|
879 |
If 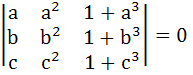 and the vectors (1, a, a2), (1, b, b2), (1, c, c2) are non-coplanar then the product abc is
If 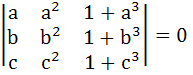 and the vectors (1, a, a2), (1, b, b2), (1, c, c2) are non-coplanar then the product abc is
|
IIT 1985 |
|
|
880 |
Let 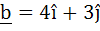 and c be two vectors perpendicular to each other in the XY–plane. All vectors in the same plane having projections 1 and 2 along b and c respectively, are given by and c be two vectors perpendicular to each other in the XY–plane. All vectors in the same plane having projections 1 and 2 along b and c respectively, are given by
Let 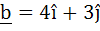 and c be two vectors perpendicular to each other in the XY–plane. All vectors in the same plane having projections 1 and 2 along b and c respectively, are given by and c be two vectors perpendicular to each other in the XY–plane. All vectors in the same plane having projections 1 and 2 along b and c respectively, are given by
|
IIT 1987 |
|
|
881 |
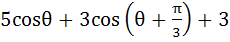 lies between –4 and 10. lies between –4 and 10.
a) True b) False
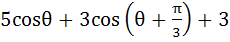 lies between –4 and 10. lies between –4 and 10.
a) True b) False
|
IIT 1979 |
|
|
882 |
Determine the smallest positive value of x (in degrees) for which 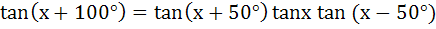 a) 30° b) 50° c) 55° d) 60°
Determine the smallest positive value of x (in degrees) for which 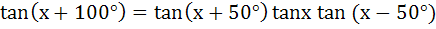 a) 30° b) 50° c) 55° d) 60°
|
IIT 1993 |
|
|
883 |
The real roots of the equation 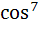 x + x + 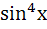 = 1 in the interval (−π, π) are …........... = 1 in the interval (−π, π) are …........... a) x = 0 b) x = ±  c) x = 0 , x = ± 
The real roots of the equation 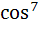 x + x + 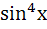 = 1 in the interval (−π, π) are …........... = 1 in the interval (−π, π) are …........... a) x = 0 b) x = ±  c) x = 0 , x = ± 
|
IIT 1997 |
|
|
884 |
The domain of the derivative of the function
f (x) =  a) R  { 0 } { 0 } b) R  c) R  d) R 
The domain of the derivative of the function
f (x) =  a) R  { 0 } { 0 } b) R  c) R  d) R 
|
IIT 2002 |
|
|
885 |
The greater of the two angles
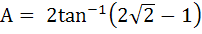 and and 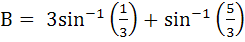 is is a) A b) B c) Both are equal
The greater of the two angles
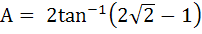 and and 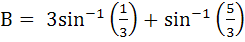 is is a) A b) B c) Both are equal
|
IIT 1989 |
|
|
886 |
If f (x) = sinx + cosx, g (x) = x2 – 1 then g ( f (x)) is invertible in the domain a)  b)  c)  d) 
If f (x) = sinx + cosx, g (x) = x2 – 1 then g ( f (x)) is invertible in the domain a)  b)  c)  d) 
|
IIT 2004 |
|
|
887 |
One or more correct answers
In a triangle the length of the two larger sides are 10 and 9 respectively. If the angles are in arithmetic progression then the length of the third side can be a) 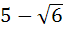 b) 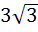 c) 5 d) 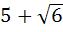 e) None of these
One or more correct answers
In a triangle the length of the two larger sides are 10 and 9 respectively. If the angles are in arithmetic progression then the length of the third side can be a) 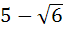 b) 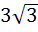 c) 5 d) 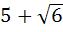 e) None of these
|
IIT 1987 |
|
|
888 |
Let f (x) = Ax2 + Bx + C where A, B , C are real numbers. Prove that if f (x) is an integer then the numbers 2A, A + B and C are all integers. Conversely prove that if the numbers 2A, A + B and C are all integers then f ( x ) is an integer whenever x is an integer.
Let f (x) = Ax2 + Bx + C where A, B , C are real numbers. Prove that if f (x) is an integer then the numbers 2A, A + B and C are all integers. Conversely prove that if the numbers 2A, A + B and C are all integers then f ( x ) is an integer whenever x is an integer.
|
IIT 1998 |
|
|
889 |
A ladder rests against a wall at an angle α to the horizontal. If its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal, then 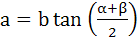 . . a) True b) False
A ladder rests against a wall at an angle α to the horizontal. If its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal, then 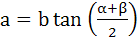 . . a) True b) False
|
IIT 1985 |
|
|
890 |
Let  be the vertices of an n sided regular polygon such that be the vertices of an n sided regular polygon such that 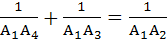 . Then find n. . Then find n. a) 5 b) 6 c) 7 d) 8
Let  be the vertices of an n sided regular polygon such that be the vertices of an n sided regular polygon such that 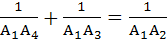 . Then find n. . Then find n. a) 5 b) 6 c) 7 d) 8
|
IIT 1994 |
|
|
891 |
A variable plane at a distance of one unit from the origin cuts the coordinate axes at A, B and C. If the centroid D(x, y, z) of triangle ABC satisfies the relation 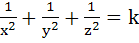 then the value of k is then the value of k is a) 9 b)  c) 1 d) 3
A variable plane at a distance of one unit from the origin cuts the coordinate axes at A, B and C. If the centroid D(x, y, z) of triangle ABC satisfies the relation 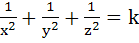 then the value of k is then the value of k is a) 9 b)  c) 1 d) 3
|
IIT 2005 |
|
|
892 |
Sketch the region bounded by the curves
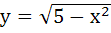 and y = |x – 1| and y = |x – 1|
and find its area. a) 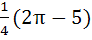 b) 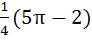 c) 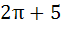 d) 5π + 2
Sketch the region bounded by the curves
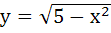 and y = |x – 1| and y = |x – 1|
and find its area. a) 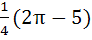 b) 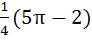 c) 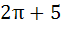 d) 5π + 2
|
IIT 1985 |
|
|
893 |
Tangents are drawn from the point (17, 7) to the circle 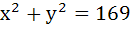 . .
Statement 1 – The tangents are mutually perpendicular, because Statement 2 – The locus of points from which mutually perpendicular tangents are drawn to the given circle is 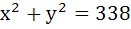 . . The question contains statement – 1 (assertion) and statement 2 (reason). Of these statements mark correct choice if a) Statement 1 and 2 are true. Statement 2 is a correct explanation for statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation for statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true
Tangents are drawn from the point (17, 7) to the circle 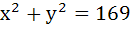 . .
Statement 1 – The tangents are mutually perpendicular, because Statement 2 – The locus of points from which mutually perpendicular tangents are drawn to the given circle is 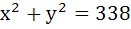 . . The question contains statement – 1 (assertion) and statement 2 (reason). Of these statements mark correct choice if a) Statement 1 and 2 are true. Statement 2 is a correct explanation for statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation for statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true
|
IIT 2007 |
|
|
894 |
Let 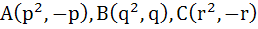 be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. a) 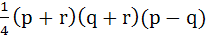 b) 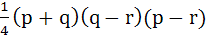 c) 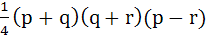 d) 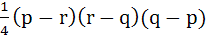
Let 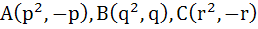 be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. be the vertices of the triangle. A parallelogram AFDE is drawn with the vertices D, E and F on the line segments BC, CA and AB respectively. Using calculus find the area of the parallelogram. a) 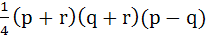 b) 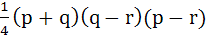 c) 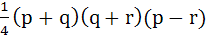 d) 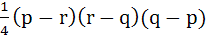
|
IIT 1986 |
|
|
895 |
Two rays in the first quadrant x + y = |a| and ax – y = 1 intersect each other in the interval a ε (a0, ∞). The value of a0 is
Two rays in the first quadrant x + y = |a| and ax – y = 1 intersect each other in the interval a ε (a0, ∞). The value of a0 is
|
IIT 2006 |
|
|
896 |
Find the area of the region bounded by the curve C: y = tanx, tangent drawn to C at 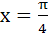 and the X–axis. and the X–axis. a) ln2 – 1 b) 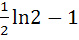 c) 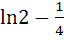 d) 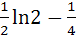
Find the area of the region bounded by the curve C: y = tanx, tangent drawn to C at 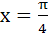 and the X–axis. and the X–axis. a) ln2 – 1 b) 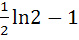 c) 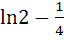 d) 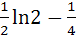
|
IIT 1988 |
|
|
897 |
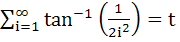 then tan t = then tan t =
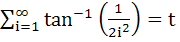 then tan t = then tan t =
|
IIT 2006 |
|
|
898 |
Sketch the curves and identify the region bounded by
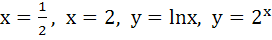
Sketch the curves and identify the region bounded by
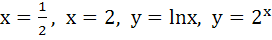
|
IIT 1991 |
|
|
899 |
Consider the following linear equations
ax + by + cz = 0
bx + cy + az = 0
cx + ay + bz = 0
Match the statements/expressions in column 1 with column 2
| Column 1 | Column2 | | i. a + b + c ≠ 0 and a2 + b2 + c2 = ab + bc + ca | A. Equations represent planes meeting at only one single point | | ii. a + b + c = 0 and a2 + b2 + c2 ≠ ab + bc + ca | B. The equations represent the line x = y = z | | iii. a + b + c ≠ 0 and a2 + b2 + c2 ≠ ab + bc + ca | C. The equations represent identical planes | | iv. a + b + c = 0 and a2 + b2 + c2 = ab + bc + ca | D.The equations represent the whole of the three dimensional space |
Consider the following linear equations
ax + by + cz = 0
bx + cy + az = 0
cx + ay + bz = 0
Match the statements/expressions in column 1 with column 2
| Column 1 | Column2 | | i. a + b + c ≠ 0 and a2 + b2 + c2 = ab + bc + ca | A. Equations represent planes meeting at only one single point | | ii. a + b + c = 0 and a2 + b2 + c2 ≠ ab + bc + ca | B. The equations represent the line x = y = z | | iii. a + b + c ≠ 0 and a2 + b2 + c2 ≠ ab + bc + ca | C. The equations represent identical planes | | iv. a + b + c = 0 and a2 + b2 + c2 = ab + bc + ca | D.The equations represent the whole of the three dimensional space |
|
IIT 2007 |
|
|
900 |
The domain of the function y(x) given by the equation 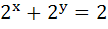 is is a) 0 < x ≤ 1 b) 0 ≤ x ≤ 1 c) 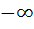 < x ≤ 0 < x ≤ 0 d) 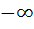 < x < 1 < x < 1
The domain of the function y(x) given by the equation 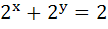 is is a) 0 < x ≤ 1 b) 0 ≤ x ≤ 1 c) 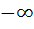 < x ≤ 0 < x ≤ 0 d) 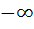 < x < 1 < x < 1
|
IIT 2000 |
|