|
726 |
If f1(x) and f2(x) are defined by domains D1 and D2 respectively then f1(x) + f2(x) is defined as on D1 ⋂ D2 a) True b) False
If f1(x) and f2(x) are defined by domains D1 and D2 respectively then f1(x) + f2(x) is defined as on D1 ⋂ D2 a) True b) False
|
IIT 1988 |
|
|
727 |
If 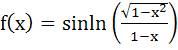 then the domain of f(x) is then the domain of f(x) is
If 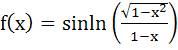 then the domain of f(x) is then the domain of f(x) is
|
IIT 1985 |
|
|
728 |
The real numbers x1, x2, x3 satisfying the equation x3 – x2 + βx + γ = 0 are in Arithmetic Progression. Find the interval in which β and γ lie.
The real numbers x1, x2, x3 satisfying the equation x3 – x2 + βx + γ = 0 are in Arithmetic Progression. Find the interval in which β and γ lie.
|
IIT 1996 |
|
|
729 |
Let p, q, r be three mutually perpendicular vectors of the same magnitude. If x satisfies the equation p 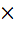 ((x – q) ((x – q)  p) + q p) + q 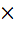 ((x – r) ((x – r) 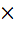 q) + r q) + r 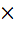 ((x – p) ((x – p) 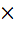 r) = 0 then x is given by r) = 0 then x is given by a) 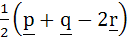 b) 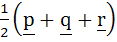 c) 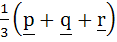 d) 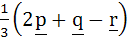
|
IIT 1997 |
|
|
730 |
Let f(x) be a non constant differentiable function defined on (−∞, ∞) such that f(x) = f(1 – x) and 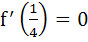 then then a) 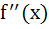 vanishes at twice an (0, 1) vanishes at twice an (0, 1) b) 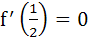 c) 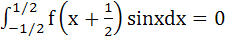 d) 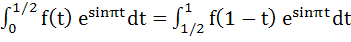
Let f(x) be a non constant differentiable function defined on (−∞, ∞) such that f(x) = f(1 – x) and 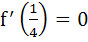 then then a) 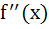 vanishes at twice an (0, 1) vanishes at twice an (0, 1) b) 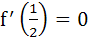 c) 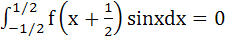 d) 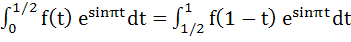
|
IIT 2008 |
|
|
731 |
Let 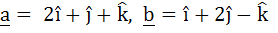 and a unit vector c be coplanar. If c is perpendicular to a then c is equal to and a unit vector c be coplanar. If c is perpendicular to a then c is equal to a) 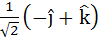 b) 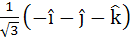 c) 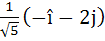 d) 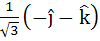
Let 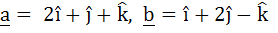 and a unit vector c be coplanar. If c is perpendicular to a then c is equal to and a unit vector c be coplanar. If c is perpendicular to a then c is equal to a) 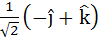 b) 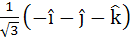 c) 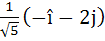 d) 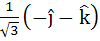
|
IIT 1999 |
|
|
732 |
Number of solutions of 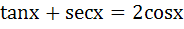 lying in the interval lying in the interval 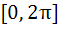 is is a) 0 b) 1 c) 2 d) 3
Number of solutions of 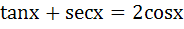 lying in the interval lying in the interval 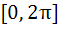 is is a) 0 b) 1 c) 2 d) 3
|
IIT 1993 |
|
|
733 |
If three complex numbers are in Arithmetic Progression, then they lie on a circle in a complex plane. a) True b) False
If three complex numbers are in Arithmetic Progression, then they lie on a circle in a complex plane. a) True b) False
|
IIT 1985 |
|
|
734 |
Multiple choice The vector 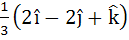 is is a) A unit vector b) Makes an angle  with the vector with the vector 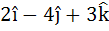 c) Parallel to vector 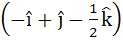 d) Perpendicular to the vector 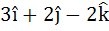
Multiple choice The vector 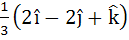 is is a) A unit vector b) Makes an angle  with the vector with the vector 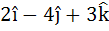 c) Parallel to vector 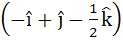 d) Perpendicular to the vector 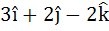
|
IIT 1994 |
|
|
735 |
A1, A2, …… , An are the vertices of a regular polygon with n sides and O is the centre. Show that
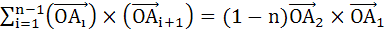
A1, A2, …… , An are the vertices of a regular polygon with n sides and O is the centre. Show that
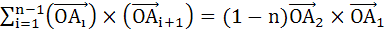
|
IIT 1982 |
|
|
736 |
If A, B, C are such that |B| = |C|. Prove that 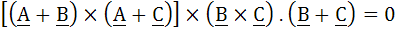
If A, B, C are such that |B| = |C|. Prove that 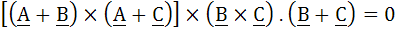
|
IIT 1997 |
|
|
737 |
Let u and v be unit vectors. If w is a vector such that 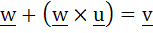 , then prove that , then prove that 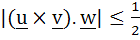 and that equality holds if and only if and that equality holds if and only if 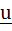 is perpendicular to is perpendicular to 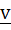
|
IIT 1999 |
|
|
738 |
Let n be an odd integer. If sin nθ = 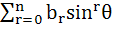 for every value of θ, then for every value of θ, then a) 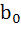 = 1, = 1, 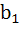 = 3 = 3 b) 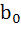 = 0, = 0, 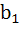 = n = n c) 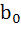 = −1, = −1, 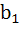 = n = n d) 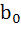 = 1, = 1, 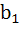 = = 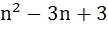
|
IIT 1998 |
|
|
739 |
The points with position vectors 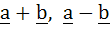 and and 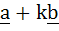 are collinear for all real values of k. are collinear for all real values of k. a) True b) False
The points with position vectors 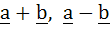 and and 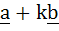 are collinear for all real values of k. are collinear for all real values of k. a) True b) False
|
IIT 1984 |
|
|
740 |
Multiple choices
Let 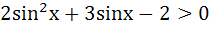 and and 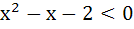 (x is measured in radians) then x lies in the interval (x is measured in radians) then x lies in the interval a) 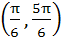 b) 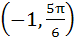 c) 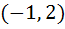 d) 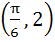
Multiple choices
Let 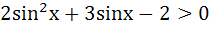 and and 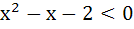 (x is measured in radians) then x lies in the interval (x is measured in radians) then x lies in the interval a) 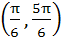 b) 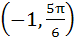 c) 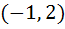 d) 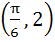
|
IIT 1994 |
|
|
741 |
If 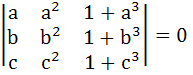 and the vectors (1, a, a2), (1, b, b2), (1, c, c2) are non-coplanar then the product abc is
If 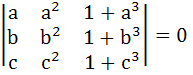 and the vectors (1, a, a2), (1, b, b2), (1, c, c2) are non-coplanar then the product abc is
|
IIT 1985 |
|
|
742 |
Let 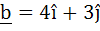 and c be two vectors perpendicular to each other in the XY–plane. All vectors in the same plane having projections 1 and 2 along b and c respectively, are given by and c be two vectors perpendicular to each other in the XY–plane. All vectors in the same plane having projections 1 and 2 along b and c respectively, are given by
Let 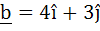 and c be two vectors perpendicular to each other in the XY–plane. All vectors in the same plane having projections 1 and 2 along b and c respectively, are given by and c be two vectors perpendicular to each other in the XY–plane. All vectors in the same plane having projections 1 and 2 along b and c respectively, are given by
|
IIT 1987 |
|
|
743 |
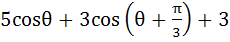 lies between –4 and 10. lies between –4 and 10.
a) True b) False
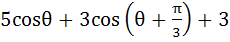 lies between –4 and 10. lies between –4 and 10.
a) True b) False
|
IIT 1979 |
|
|
744 |
Let the vectors  represent the edges of a regular hexagon represent the edges of a regular hexagon Statement 1 -  because because Statement 2 -  a) Statement 1 and 2 are true and Statement 2 is a correct explanation of statement 1. b) Statement 1 and 2 are true and Statement 2 is not a correct explanation of statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
Let the vectors  represent the edges of a regular hexagon represent the edges of a regular hexagon Statement 1 -  because because Statement 2 -  a) Statement 1 and 2 are true and Statement 2 is a correct explanation of statement 1. b) Statement 1 and 2 are true and Statement 2 is not a correct explanation of statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
|
IIT 2007 |
|
|
745 |
Find the smallest possible value of p for which the equation
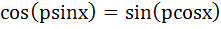 a) 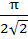 b) 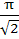 c)  d) 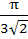
Find the smallest possible value of p for which the equation
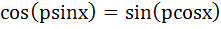 a) 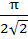 b) 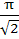 c)  d) 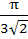
|
IIT 1995 |
|
|
746 |
If f (x) =  for every real x then the minimum value of f for every real x then the minimum value of f a) does not exist because f is unbounded b) is not attained even though f is bounded c) is equal to 1 d) is equal to −1
If f (x) =  for every real x then the minimum value of f for every real x then the minimum value of f a) does not exist because f is unbounded b) is not attained even though f is bounded c) is equal to 1 d) is equal to −1
|
IIT 1998 |
|
|
747 |
Find the larger of cos(lnθ) and ln(cosθ) if 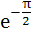 < θ < < θ <  . . a) cos(lnθ) b) ln(cosθ) c) Neither is larger throughout the interval
Find the larger of cos(lnθ) and ln(cosθ) if 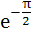 < θ < < θ <  . . a) cos(lnθ) b) ln(cosθ) c) Neither is larger throughout the interval
|
IIT 1983 |
|
|
748 |
If the function f : [ 1, 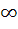 ) → [ 1, ) → [ 1, 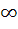 ) is defined by f (x) = 2x(x – 1) then ) is defined by f (x) = 2x(x – 1) then
f -1(x) is a) 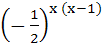 b)  ( (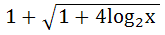 ) ) c)  ( (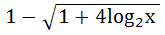 ) ) d) 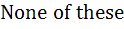
|
IIT 1999 |
|
|
749 |
If 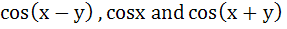 are in harmonic progression then are in harmonic progression then 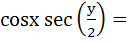 ………… ………… a) 1 b) 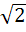 c) 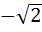 d) 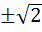
If 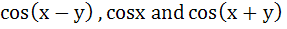 are in harmonic progression then are in harmonic progression then 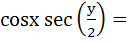 ………… ………… a) 1 b) 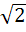 c) 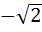 d) 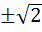
|
IIT 1997 |
|
|
750 |
If 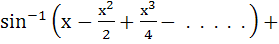 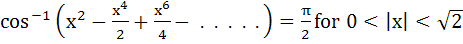
then x equals a)  b) 1 c) 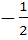 d) –1
If 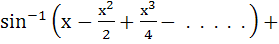 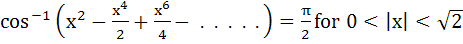
then x equals a)  b) 1 c) 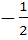 d) –1
|
IIT 1999 |
|