|
601 |
If 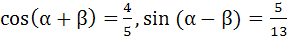 and α, β lie between 0 and and α, β lie between 0 and 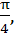 find find 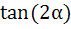 a) 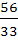 b) 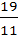 c)  d) 2
If 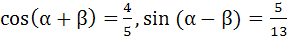 and α, β lie between 0 and and α, β lie between 0 and 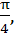 find find 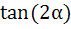 a) 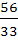 b) 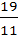 c)  d) 2
|
IIT 1979 |
03:00 min
|
|
602 |
The product of n positive real numbers is unity. Then their sum is a) A positive integer b) Divisible by n c) Equal to 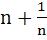 d) Never less than n
The product of n positive real numbers is unity. Then their sum is a) A positive integer b) Divisible by n c) Equal to 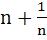 d) Never less than n
|
IIT 1991 |
00:53 min
|
|
603 |
If 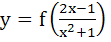 and and 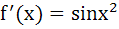 , then find , then find 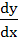
|
IIT 1982 |
01:40 min
|
|
604 |
The integral 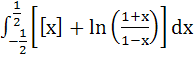 equals equals a)  b) 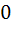 c) 1 d) 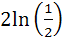
The integral 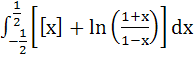 equals equals a)  b) 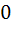 c) 1 d) 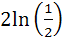
|
IIT 2002 |
03:16 min
|
|
605 |
The inequality |z – 4| < |z – 2| represents the region given by a) Re(z) ≥ 0 b) Re(z) < 0 c) Re(z) > 0 d) None of these
The inequality |z – 4| < |z – 2| represents the region given by a) Re(z) ≥ 0 b) Re(z) < 0 c) Re(z) > 0 d) None of these
|
IIT 1982 |
01:58 min
|
|
606 |
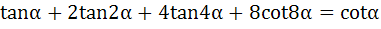
a) True b) False
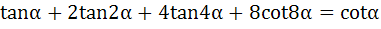
a) True b) False
|
IIT 1988 |
03:38 min
|
|
607 |
Coefficient of t24 in (1 + t2)12 (1 + t12) (1 + t24) is a) 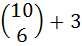 b) 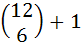 c) 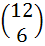 d) 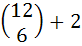
Coefficient of t24 in (1 + t2)12 (1 + t12) (1 + t24) is a) 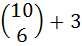 b) 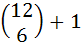 c) 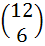 d) 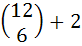
|
IIT 2003 |
03:19 min
|
|
608 |
If f (x) = |x – 2| and g (x) = 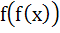 then then 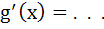 for x > 20 for x > 20 a) 0 b) 1 c) 2 d) 4
If f (x) = |x – 2| and g (x) = 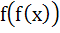 then then 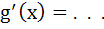 for x > 20 for x > 20 a) 0 b) 1 c) 2 d) 4
|
IIT 1990 |
01:14 min
|
|
609 |
The value of the integral 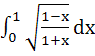 is is a) 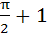 b) 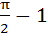 c) 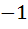 d) 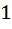
The value of the integral 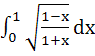 is is a) 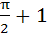 b) 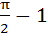 c) 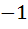 d) 
|
IIT 2004 |
02:02 min
|
|
610 |
If tan A 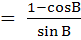 then then 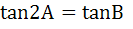 a) True b) False
If tan A 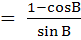 then then 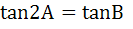 a) True b) False
|
IIT 1980 |
01:00 min
|
|
611 |
For a real y, let [y] denote the greatest integer less than or equal to y. Then the function 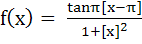 is is a) Discontinuous at some x b) Continuous at all x but the derivative 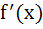 does not exist for some x does not exist for some x c) 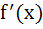 exists for all x but the derivative exists for all x but the derivative 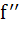 does not exist for some x does not exist for some x d) 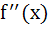 exists for all x exists for all x
For a real y, let [y] denote the greatest integer less than or equal to y. Then the function 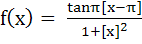 is is a) Discontinuous at some x b) Continuous at all x but the derivative 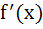 does not exist for some x does not exist for some x c) 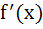 exists for all x but the derivative exists for all x but the derivative 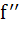 does not exist for some x does not exist for some x d) 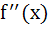 exists for all x exists for all x
|
IIT 1981 |
02:16 min
|
|
612 |
Show that 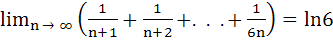
Show that 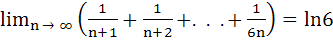
|
IIT 1981 |
01:28 min
|
|
613 |
The position vectors of the point A, B, C, D are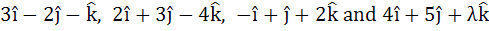 respectively. If the points A, B, C and D lie in a plane, find the value of λ. respectively. If the points A, B, C and D lie in a plane, find the value of λ.
The position vectors of the point A, B, C, D are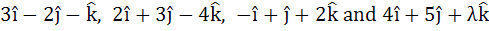 respectively. If the points A, B, C and D lie in a plane, find the value of λ. respectively. If the points A, B, C and D lie in a plane, find the value of λ.
|
IIT 1986 |
03:41 min
|
|
614 |
If k = 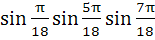 then the numerical value of k is ………. then the numerical value of k is ………. a)  b)  c)  d) 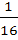
If k = 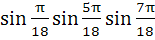 then the numerical value of k is ………. then the numerical value of k is ………. a)  b)  c)  d) 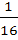
|
IIT 1993 |
02:32 min
|
|
615 |
If f (a) = 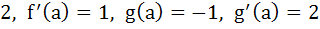 then the value of then the value of 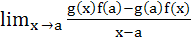 is is a) – 5 b)  c) 5 d) None of these
If f (a) = 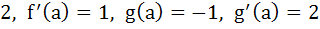 then the value of then the value of 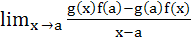 is is a) – 5 b)  c) 5 d) None of these
|
IIT 1983 |
01:55 min
|
|
616 |
Evaluate 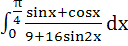 a) 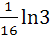 b) 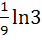 c) 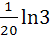 d) 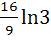
|
IIT 1983 |
05:32 min
|
|
617 |
Let A = 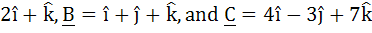 . Determine a vector R satisfying . Determine a vector R satisfying 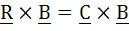 and and 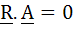 . .
|
IIT 1990 |
03:53 min
|
|
618 |
If a, b, c are in Arithmetic Progression then the straight line
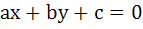 will pass through a fixed point whose coordinates are . . . . . will pass through a fixed point whose coordinates are . . . . .
If a, b, c are in Arithmetic Progression then the straight line
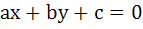 will pass through a fixed point whose coordinates are . . . . . will pass through a fixed point whose coordinates are . . . . .
|
IIT 1984 |
01:35 min
|
|
619 |
If 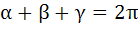 then then tan 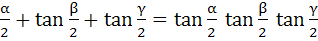 a) True b) False
If 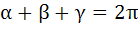 then then tan 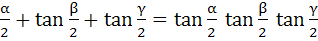 a) True b) False
|
IIT 1979 |
01:42 min
|
|
620 |
Evaluate 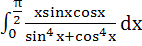 a) 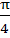 b) 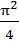 c) 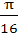 d) 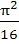
|
IIT 1985 |
04:33 min
|
|
621 |
Let C be the curve 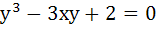 . If H is the set of points on the curve C when the tangent is horizontal and v be the set of all points on the curve C when the tangent is vertical then H = . . . . . and v = . . . . . . If H is the set of points on the curve C when the tangent is horizontal and v be the set of all points on the curve C when the tangent is vertical then H = . . . . . and v = . . . . .
Let C be the curve 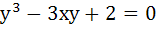 . If H is the set of points on the curve C when the tangent is horizontal and v be the set of all points on the curve C when the tangent is vertical then H = . . . . . and v = . . . . . . If H is the set of points on the curve C when the tangent is horizontal and v be the set of all points on the curve C when the tangent is vertical then H = . . . . . and v = . . . . .
|
IIT 1994 |
04:09 min
|
|
622 |
In a triangle ABC, angle A is greater than angle B. If the measures of angle A and B satisfy the equation 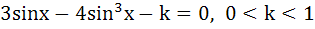 , then the measure of angle C is , then the measure of angle C is a)  b)  c) 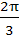 d) 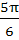
In a triangle ABC, angle A is greater than angle B. If the measures of angle A and B satisfy the equation 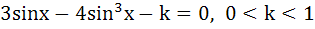 , then the measure of angle C is , then the measure of angle C is a)  b)  c) 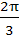 d) 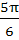
|
IIT 1990 |
01:43 min
|
|
623 |
Prove that C0 – 22C1 + 32C2 − . . . + (−)n (n + 1)2 Cn = 0 for n > 2 where 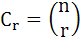
Prove that C0 – 22C1 + 32C2 − . . . + (−)n (n + 1)2 Cn = 0 for n > 2 where 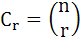
|
IIT 1989 |
05:31 min
|
|
624 |
Show that 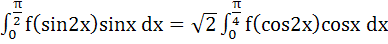
Show that 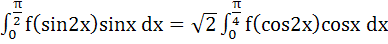
|
IIT 1990 |
05:42 min
|
|
625 |
The centre of the circle passing through (0, 1) and touching the curve 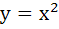 at (2, 4) is at (2, 4) is a) 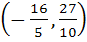 b) 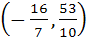 c) 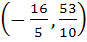 d) None of these
The centre of the circle passing through (0, 1) and touching the curve 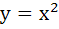 at (2, 4) is at (2, 4) is a) 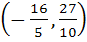 b) 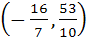 c) 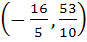 d) None of these
|
IIT 1983 |
07:23 min
|