|
526 |
The domain of f (x) = 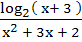 is is a) R – {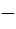 1, 1, 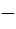 2} 2} b) ( 2, 2, 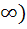 c) R – { 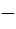 1, 1, 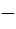 2, 2, 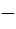 3} 3} d) (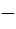 3, 3, 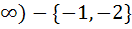
|
IIT 2001 |
01:19 min
|
|
527 |
Let 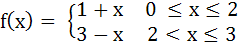 Determine the function g (x) = f (f(x)) and hence find the points of discontinuity of g if any. a) g(x) is continuous for all x except x = 1 and x = 2 b) g(x) is continuous for all x except x = 1 c) g(x) is continuous for all x except x = 2 d) g(x) is continuous for all x
Let 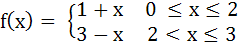 Determine the function g (x) = f (f(x)) and hence find the points of discontinuity of g if any. a) g(x) is continuous for all x except x = 1 and x = 2 b) g(x) is continuous for all x except x = 1 c) g(x) is continuous for all x except x = 2 d) g(x) is continuous for all x
|
IIT 1983 |
05:15 min
|
|
528 |
The slope of the tangent to the curve y = f(x) at [x, f(x)] is 2x + 1. The curve passes through (1, 2), then the area bounded by the curve and X–axis, and the line x = 1 is a)  b)  c)  d) 6
The slope of the tangent to the curve y = f(x) at [x, f(x)] is 2x + 1. The curve passes through (1, 2), then the area bounded by the curve and X–axis, and the line x = 1 is a)  b)  c)  d) 6
|
IIT 1995 |
03:15 min
|
|
529 |
Three circles touch each other externally. The tangents at their points of contact meet at a point whose distance from a point of contact is 4. Find the ratio of the product of the radii to the sum of the radii of the circles.
Three circles touch each other externally. The tangents at their points of contact meet at a point whose distance from a point of contact is 4. Find the ratio of the product of the radii to the sum of the radii of the circles.
|
IIT 1992 |
07:55 min
|
|
530 |
The number of solutions of 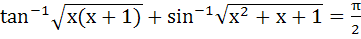 is is a) 0 b) One c) Two d) Infinite
The number of solutions of 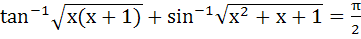 is is a) 0 b) One c) Two d) Infinite
|
IIT 2001 |
04:00 min
|
|
531 |
Let f (x) be a continuous function satisfying 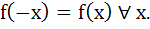 If If 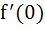 exists, find its value. exists, find its value. a) 0 b) 1 c) 2 d) 4
Let f (x) be a continuous function satisfying 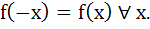 If If 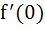 exists, find its value. exists, find its value. a) 0 b) 1 c) 2 d) 4
|
IIT 1987 |
03:18 min
|
|
532 |
The letters of the word COCHIN are permuted and all permutations are arranged in an alphabetical order as in the English dictionary. The number of words that appear before the word COCHIN is a) 360 b) 192 c) 96 d) 48
The letters of the word COCHIN are permuted and all permutations are arranged in an alphabetical order as in the English dictionary. The number of words that appear before the word COCHIN is a) 360 b) 192 c) 96 d) 48
|
IIT 2007 |
03:06 min
|
|
533 |
Five balls of different colours are to be placed in three boxes of different sizes. Each box can hold all five balls. In how many different ways can we place the balls so that no box is empty?
Five balls of different colours are to be placed in three boxes of different sizes. Each box can hold all five balls. In how many different ways can we place the balls so that no box is empty?
|
IIT 1981 |
07:04 min
|
|
534 |
If 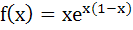 then f(x) is then f(x) is a) Increasing on 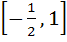 b) Decreasing on ℝ c) Increasing on ℝ d) Decreasing on 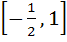
If 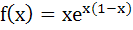 then f(x) is then f(x) is a) Increasing on 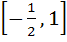 b) Decreasing on ℝ c) Increasing on ℝ d) Decreasing on 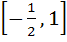
|
IIT 2001 |
02:04 min
|
|
535 |
In a triangle ABC, ∠ B =  , ∠ C = , ∠ C = 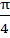 . Let D divides BC internally in the ratio 1:3 then . Let D divides BC internally in the ratio 1:3 then 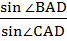 is equal to is equal to a) 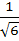 b)  c) 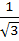 d) 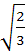
In a triangle ABC, ∠ B =  , ∠ C = , ∠ C = 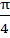 . Let D divides BC internally in the ratio 1:3 then . Let D divides BC internally in the ratio 1:3 then 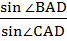 is equal to is equal to a) 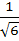 b)  c) 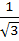 d) 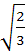
|
IIT 1995 |
03:14 min
|
|
536 |
Let 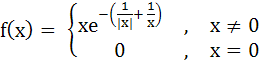 Test whether f(x) is continuous at x = 0 f(x) is differentiable at x = 0 a) f(x) is differentiable and continuous at x = 0 b) f(x) is continuous but not differentiable at x = 0 c) f(x) is neither continuous nor differentiable at x = 0
Let 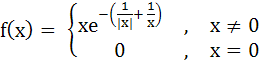 Test whether f(x) is continuous at x = 0 f(x) is differentiable at x = 0 a) f(x) is differentiable and continuous at x = 0 b) f(x) is continuous but not differentiable at x = 0 c) f(x) is neither continuous nor differentiable at x = 0
|
IIT 1994 |
05:27 min
|
|
537 |
A student is allowed to select at most n books from a collection of (2n + 1) books. If the total number of ways in which he can select at least one book is 63, find the value of n?
A student is allowed to select at most n books from a collection of (2n + 1) books. If the total number of ways in which he can select at least one book is 63, find the value of n?
|
IIT 1987 |
06:50 min
|
|
538 |
Let 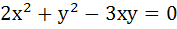 be the equation of pair of tangents from the origin O to a circle of radius 3 with centre in the first quadrant. If A is a point of contact, find the length of OA. be the equation of pair of tangents from the origin O to a circle of radius 3 with centre in the first quadrant. If A is a point of contact, find the length of OA.
Let 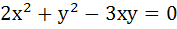 be the equation of pair of tangents from the origin O to a circle of radius 3 with centre in the first quadrant. If A is a point of contact, find the length of OA. be the equation of pair of tangents from the origin O to a circle of radius 3 with centre in the first quadrant. If A is a point of contact, find the length of OA.
|
IIT 2001 |
04:52 min
|
|
539 |
If the angles of a triangle are in the ratio 4:1:1 then the ratio of the longest side to the perimeter is a) 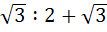 b) 1 : 6 c) 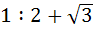 d) 2 : 3
If the angles of a triangle are in the ratio 4:1:1 then the ratio of the longest side to the perimeter is a) 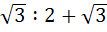 b) 1 : 6 c) 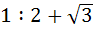 d) 2 : 3
|
IIT 2003 |
03:18 min
|
|
540 |
If f (x) = cos [π2] x + cos [-π2] x where [x] stands of the greatest integer function then a) f 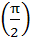 = −1 = −1 b) 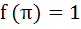 c) f (−π) = 0 d) f 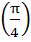 = 1 = 1
If f (x) = cos [π2] x + cos [-π2] x where [x] stands of the greatest integer function then a) f 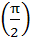 = −1 = −1 b) 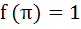 c) f (−π) = 0 d) f 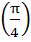 = 1 = 1
|
IIT 1991 |
03:36 min
|
|
541 |
Let p be a prime and m be a positive integer. By mathematical induction on m, or otherwise, prove that whenever r is an integer such that p does not divide r, p divides 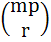
Let p be a prime and m be a positive integer. By mathematical induction on m, or otherwise, prove that whenever r is an integer such that p does not divide r, p divides 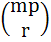
|
IIT 1998 |
03:45 min
|
|
542 |
Let In represents area of n sided regular polygon inscribed in a unit circle and On the area of n–sided regular polygon circumscribing it. Prove that 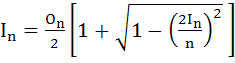
Let In represents area of n sided regular polygon inscribed in a unit circle and On the area of n–sided regular polygon circumscribing it. Prove that 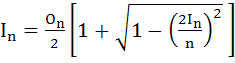
|
IIT 2003 |
07:43 min
|
|
543 |
P(x) is a polynomial function such that P(1) = 0, 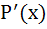 > P(x) > P(x) 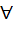 x > 1. Then x > 1. Then 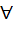 x > 1, x > 1,
a) P(x) > 0 b) P(x) = 0 c) P(x) < 1
P(x) is a polynomial function such that P(1) = 0, 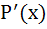 > P(x) > P(x) 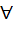 x > 1. Then x > 1. Then 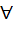 x > 1, x > 1,
a) P(x) > 0 b) P(x) = 0 c) P(x) < 1
|
IIT 2003 |
02:15 min
|
|
544 |
Prove that
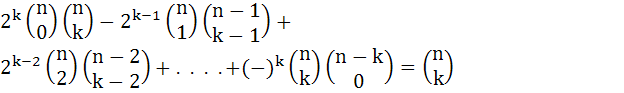
Prove that
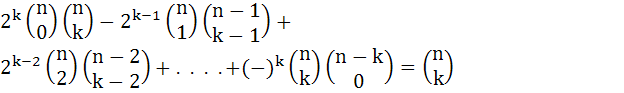
|
IIT 2003 |
05:28 min
|
|
545 |
Minimum area of the triangle formed by the tangent to the ellipse  with co-ordinate axes is with co-ordinate axes is
a) 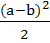 b) 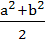 c) 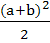 d) ab
Minimum area of the triangle formed by the tangent to the ellipse  with co-ordinate axes is with co-ordinate axes is
a) 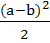 b) 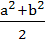 c) 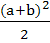 d) ab
|
IIT 2005 |
02:43 min
|
|
546 |
If A and B are points in the plane such that 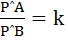 (constant) for all P on a given circle then the value of k cannot be equal to - - - - -. (constant) for all P on a given circle then the value of k cannot be equal to - - - - -.
If A and B are points in the plane such that 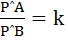 (constant) for all P on a given circle then the value of k cannot be equal to - - - - -. (constant) for all P on a given circle then the value of k cannot be equal to - - - - -.
|
IIT 1982 |
04:30 min
|
|
547 |
Let {x} and [x] denote the fractional and integral part of a real number respectively. Solve 4 {x} = x + [x] a) x = 0 b) 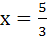 c) 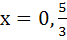 d) 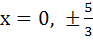
Let {x} and [x] denote the fractional and integral part of a real number respectively. Solve 4 {x} = x + [x] a) x = 0 b) 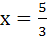 c) 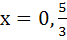 d) 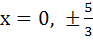
|
IIT 1994 |
03:11 min
|
|
548 |
The sides AB, BC and CA of a triangle ABC have 3, 4 and 5 interior points respectively on them. The number of triangles that can be constructed using these interior points as vertices is . . . .
The sides AB, BC and CA of a triangle ABC have 3, 4 and 5 interior points respectively on them. The number of triangles that can be constructed using these interior points as vertices is . . . .
|
IIT 1984 |
04:31 min
|
|
549 |
Multiple choice Let h(x) = f(x) – (f(x))2 + (f(x))3 for every real number x, then a) h increases whenever f is increasing b) h is increasing whenever f is decreasing c) h is decreasing whenever f is decreasing d) nothing can be said in general
Multiple choice Let h(x) = f(x) – (f(x))2 + (f(x))3 for every real number x, then a) h increases whenever f is increasing b) h is increasing whenever f is decreasing c) h is decreasing whenever f is decreasing d) nothing can be said in general
|
IIT 1998 |
02:37 min
|
|
550 |
From the origin chords are drawn to the circle  . The equation of the locus of the mid points of these chords is . . . . . . The equation of the locus of the mid points of these chords is . . . . .
From the origin chords are drawn to the circle  . The equation of the locus of the mid points of these chords is . . . . . . The equation of the locus of the mid points of these chords is . . . . .
|
IIT 1984 |
02:45 min
|