|
226 |
If y is a function of x and ln (x + y) – 2xy = 0 then the value of y’ (0) is equal to a) 1 b) – 1 c) 2 d) 0
If y is a function of x and ln (x + y) – 2xy = 0 then the value of y’ (0) is equal to a) 1 b) – 1 c) 2 d) 0
|
IIT 2004 |
01:56 min
|
|
227 |
If 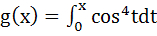 then g(x + π) equals then g(x + π) equals a) g(x) + g(π) b) g(x) − g(π) c) g(x) g(π) d) 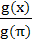
If 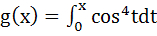 then g(x + π) equals then g(x + π) equals a) g(x) + g(π) b) g(x) − g(π) c) g(x) g(π) d) 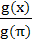
|
IIT 1997 |
05:05 min
|
|
228 |
If 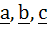 are unit vectors, then are unit vectors, then 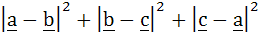 does not exceed does not exceed a) 4 b) 9 c) 8 d) 6
If 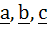 are unit vectors, then are unit vectors, then 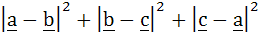 does not exceed does not exceed a) 4 b) 9 c) 8 d) 6
|
IIT 2001 |
04:28 min
|
|
229 |
In a city only two news papers A and B are published. It is known that 25% of the city population read A and 20% read B, while 8% read A and B. It is also known that 30% of those who read A but not B and 40% of those who read B but not A look into the advertisement. 50% of those who read both A and B look into the advertisement. What is the percentage of the population that reads an advertisement?
In a city only two news papers A and B are published. It is known that 25% of the city population read A and 20% read B, while 8% read A and B. It is also known that 30% of those who read A but not B and 40% of those who read B but not A look into the advertisement. 50% of those who read both A and B look into the advertisement. What is the percentage of the population that reads an advertisement?
|
IIT 1984 |
02:57 min
|
|
230 |
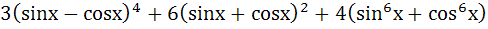
a) 11 b) 12 c) 13 d) 14
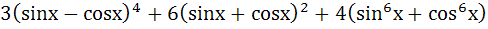
a) 11 b) 12 c) 13 d) 14
|
IIT 1995 |
04:20 min
|
|
231 |
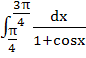 is equal to is equal to
a) 2 b) –2 c)  d) 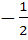
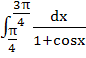 is equal to is equal to
a) 2 b) –2 c)  d) 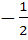
|
IIT 1999 |
03:25 min
|
|
232 |
Let 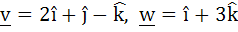 and u is a unit vector then the maximum value of and u is a unit vector then the maximum value of 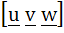 is is a) 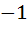 b) 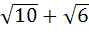 c)  d) 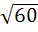
Let 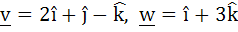 and u is a unit vector then the maximum value of and u is a unit vector then the maximum value of 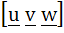 is is a) 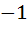 b) 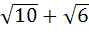 c)  d) 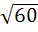
|
IIT 2003 |
02:32 min
|
|
233 |
Given both θ and Ф are acute angles and sinθ =  , cos Ф = , cos Ф =  then the value of θ + Ф belongs to then the value of θ + Ф belongs to a) 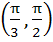 b) 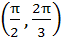 c) 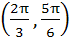 d) 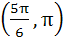
Given both θ and Ф are acute angles and sinθ =  , cos Ф = , cos Ф =  then the value of θ + Ф belongs to then the value of θ + Ф belongs to a) 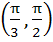 b) 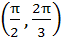 c) 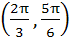 d) 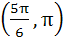
|
IIT 2004 |
02:15 min
|
|
234 |
Let x be the Arithmetic Mean and y, z be two Geometric Means between any two positive numbers then 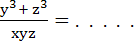
Let x be the Arithmetic Mean and y, z be two Geometric Means between any two positive numbers then 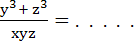
|
IIT 1997 |
02:27 min
|
|
235 |
The value of the integral 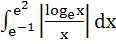 a)  b)  c) 3 d) 5
The value of the integral 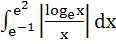 a)  b)  c) 3 d) 5
|
IIT 2000 |
06:09 min
|
|
236 |
Let 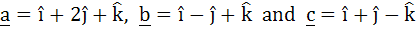 . A vector in the plane of a and b whose projection on c is . A vector in the plane of a and b whose projection on c is 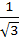 is is a) 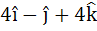 b) 3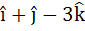 c) 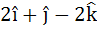 d) 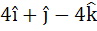
Let 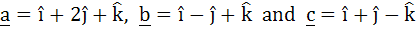 . A vector in the plane of a and b whose projection on c is . A vector in the plane of a and b whose projection on c is 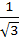 is is a) 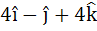 b) 3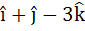 c) 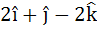 d) 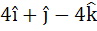
|
IIT 2006 |
03:33 min
|
|
237 |
If 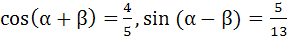 and α, β lie between 0 and and α, β lie between 0 and 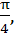 find find 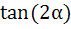 a) 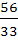 b) 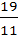 c)  d) 2
If 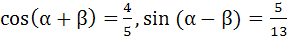 and α, β lie between 0 and and α, β lie between 0 and 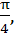 find find 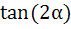 a) 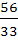 b) 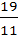 c)  d) 2
|
IIT 1979 |
03:00 min
|
|
238 |
The product of n positive real numbers is unity. Then their sum is a) A positive integer b) Divisible by n c) Equal to 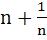 d) Never less than n
The product of n positive real numbers is unity. Then their sum is a) A positive integer b) Divisible by n c) Equal to 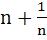 d) Never less than n
|
IIT 1991 |
00:53 min
|
|
239 |
If 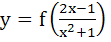 and and 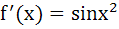 , then find , then find 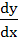
|
IIT 1982 |
01:40 min
|
|
240 |
The integral 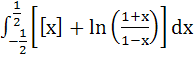 equals equals a)  b) 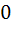 c) 1 d) 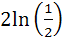
The integral 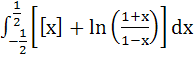 equals equals a)  b) 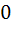 c) 1 d) 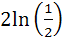
|
IIT 2002 |
03:16 min
|
|
241 |
The inequality |z – 4| < |z – 2| represents the region given by a) Re(z) ≥ 0 b) Re(z) < 0 c) Re(z) > 0 d) None of these
The inequality |z – 4| < |z – 2| represents the region given by a) Re(z) ≥ 0 b) Re(z) < 0 c) Re(z) > 0 d) None of these
|
IIT 1982 |
01:58 min
|
|
242 |
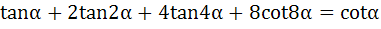
a) True b) False
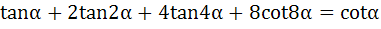
a) True b) False
|
IIT 1988 |
03:38 min
|
|
243 |
Coefficient of t24 in (1 + t2)12 (1 + t12) (1 + t24) is a) 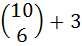 b) 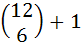 c) 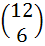 d) 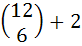
Coefficient of t24 in (1 + t2)12 (1 + t12) (1 + t24) is a) 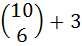 b) 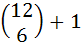 c) 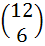 d) 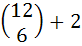
|
IIT 2003 |
03:19 min
|
|
244 |
If f (x) = |x – 2| and g (x) = 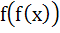 then then 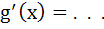 for x > 20 for x > 20 a) 0 b) 1 c) 2 d) 4
If f (x) = |x – 2| and g (x) = 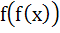 then then 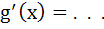 for x > 20 for x > 20 a) 0 b) 1 c) 2 d) 4
|
IIT 1990 |
01:14 min
|
|
245 |
The value of the integral 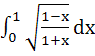 is is a) 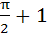 b) 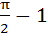 c) 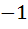 d) 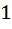
The value of the integral 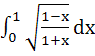 is is a) 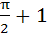 b) 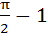 c) 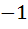 d) 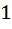
|
IIT 2004 |
02:02 min
|
|
246 |
If tan A 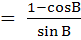 then then 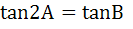 a) True b) False
If tan A 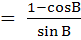 then then 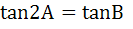 a) True b) False
|
IIT 1980 |
01:00 min
|
|
247 |
For a real y, let [y] denote the greatest integer less than or equal to y. Then the function 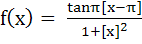 is is a) Discontinuous at some x b) Continuous at all x but the derivative 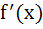 does not exist for some x does not exist for some x c) 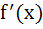 exists for all x but the derivative exists for all x but the derivative 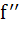 does not exist for some x does not exist for some x d) 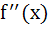 exists for all x exists for all x
For a real y, let [y] denote the greatest integer less than or equal to y. Then the function 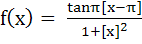 is is a) Discontinuous at some x b) Continuous at all x but the derivative 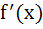 does not exist for some x does not exist for some x c) 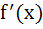 exists for all x but the derivative exists for all x but the derivative 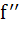 does not exist for some x does not exist for some x d) 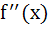 exists for all x exists for all x
|
IIT 1981 |
02:16 min
|
|
248 |
Show that 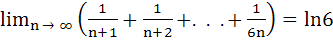
Show that 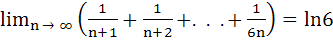
|
IIT 1981 |
01:28 min
|
|
249 |
The position vectors of the point A, B, C, D are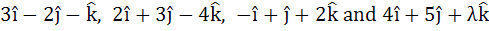 respectively. If the points A, B, C and D lie in a plane, find the value of λ. respectively. If the points A, B, C and D lie in a plane, find the value of λ.
The position vectors of the point A, B, C, D are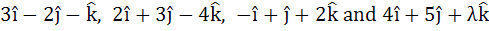 respectively. If the points A, B, C and D lie in a plane, find the value of λ. respectively. If the points A, B, C and D lie in a plane, find the value of λ.
|
IIT 1986 |
03:41 min
|
|
250 |
If k = 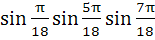 then the numerical value of k is ………. then the numerical value of k is ………. a)  b)  c)  d) 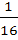
If k = 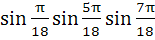 then the numerical value of k is ………. then the numerical value of k is ………. a)  b)  c)  d) 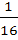
|
IIT 1993 |
02:32 min
|